Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les fonctions en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Fonction monotone, réciproque et bornée
1. Fonctions monotones
2. Fonction réciproque
3. Fonction bornée
4. Équations fonctionnelles
5. Avec la partie entière
6. Calculs de dérivées
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Fonctions monotones
Exercice 1
Soit ![]() une fonction croissante sur
une fonction croissante sur ![]() à valeurs dans
à valeurs dans ![]() telle qu’il existe
telle qu’il existe ![]() tel que
tel que ![]() .
.
![]() est constante sur
est constante sur ![]() . Vrai ou faux ?
. Vrai ou faux ?
Correction :
![]() Soit pour
Soit pour ![]() ,
, ![]() :
: ![]() .
.
![]()
![]() est vraie car
est vraie car ![]()
![]() On suppose que
On suppose que ![]() est vraie, en utilisant l’hypothèse de récurrence avec
est vraie, en utilisant l’hypothèse de récurrence avec ![]() ,
, ![]() donc
donc ![]() .
.
![]() est vérifiée.
est vérifiée.
![]() Comme
Comme ![]() , pour tout
, pour tout ![]() , il existe
, il existe ![]() tel que
tel que ![]()
par croissance de ![]() :
:![]() .
.
donc ![]() .
.
On a montré que ![]() est constante sur
est constante sur ![]() .
.
Exercice 2
Soit ![]() une fonction croissante de
une fonction croissante de ![]() dans
dans ![]() .
.
Il existe ![]() tel que
tel que ![]() .
.
indication : introduire ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
![]()
![]() , donc
, donc ![]() .
.
![]() est une partie non vide de
est une partie non vide de ![]() , minorée par
, minorée par ![]() .
.
![]() admet une borne inférieure
admet une borne inférieure ![]() .
.
![]() Si
Si ![]() ,
, ![]() ,
,
comme ![]() est la borne inférieure de
est la borne inférieure de ![]() et
et ![]() ,
, ![]() n’est pas un minorant de
n’est pas un minorant de ![]() , donc il existe
, donc il existe ![]() tel que
tel que ![]() .
.
Par croissance de ![]() ,
, ![]()
et ![]() car
car ![]() ,
,
on en déduit que ![]() , ce qui est absurde.
, ce qui est absurde.
Donc on a prouvé que ![]() et donc
et donc ![]() .
.
![]() Si l’on avait
Si l’on avait ![]() , par croissance de
, par croissance de ![]() , on aurait
, on aurait ![]() , donc
, donc ![]() .
.
![]() serait un élément de
serait un élément de ![]() strictement inférieure à la borne inférieure de
strictement inférieure à la borne inférieure de ![]() , ce qui est impossible.
, ce qui est impossible.
Il est impossible d’avoir ![]() , comme
, comme ![]() , on a prouvé que
, on a prouvé que ![]() .
.
Donc ![]() admet un point fixe sur
admet un point fixe sur ![]() .
.
2. Fonction réciproque
Exercice 1
![]()
Montrer que ![]() admet une fonction réciproque que l’on déterminera.
admet une fonction réciproque que l’on déterminera.
Correction : ![]()
![]() admet une fonction réciproque définie sur
admet une fonction réciproque définie sur ![]() .
.
![]() est continue sur
est continue sur ![]() , dérivable et
, dérivable et
![]()
![]() est strictement croissante,
est strictement croissante, ![]() et
et ![]()
donc ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
![]() Fonction réciproque
Fonction réciproque
On résout l’équation ![]() ssi
ssi
![]() ssi
ssi ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
![]() Si
Si ![]() , l’équation du second degré admet deux racines de produit égal à
, l’équation du second degré admet deux racines de produit égal à ![]() donc de signe différent (
donc de signe différent (![]() )
)
![]()
![]() et
et ![]()
Lorsque ![]() ,
, ![]()
![]() et
et ![]() et
et ![]() sont de signe contraire, alors
sont de signe contraire, alors ![]() donc la racine à retenir est
donc la racine à retenir est ![]() .
.
Lorsque ![]() ,
, ![]()
![]() et
et ![]() et
et ![]() sont de signe contraire, alors
sont de signe contraire, alors ![]() donc la racine à retenir est
donc la racine à retenir est ![]() .
.
La fonction réciproque est définie par ![]() si
si ![]() et
et ![]() .
.
Exercice 2
Soit ![]() définie sur
définie sur ![]() par
par ![]()
Question 1
![]() est-elle dérivable sur
est-elle dérivable sur ![]() ?
?
Correction : Il est évident que ![]() est dérivable sur
est dérivable sur ![]() .
.
On étudie le taux d’accroissement de ![]() en
en ![]() :
:
![]()
comme ![]() ,
, ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
Exercice 2 (fin)
Question 2
Montrer que ![]() définit une bijection et déterminer
définit une bijection et déterminer ![]() .
.
Correction : ![]() Définition et stricte monotonie de
Définition et stricte monotonie de ![]() .
.
![]() est définie sur
est définie sur ![]() et continue,
et continue, ![]() est impaire.
est impaire.
![]() Si
Si ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
![]() Si
Si ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
![]()
![]() .
.
On a prouvé que ![]() est strictement croissante sur
est strictement croissante sur ![]() .
.
![]()
![]() est continue et strictement croissante sur
est continue et strictement croissante sur ![]() .
.
![]() ,
, ![]()
donc ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
![]() Fonction réciproque
Fonction réciproque
![]()
![]() donc
donc ![]() .
.
![]() Si
Si ![]()
On résout ![]()
ssi ![]() ssi
ssi ![]() ssi
ssi ![]()
![]()
![]() Si
Si ![]()
On résout ![]()
ssi ![]() ssi
ssi ![]() ssi
ssi ![]()
![]()
On a prouvé que pour tout réel ![]() ,
, ![]() .
.
donc ![]() .
.
Exercice 3
On note ![]() .
.
Question 1
![]() admet une fonction réciproque
admet une fonction réciproque ![]() définie sur
définie sur ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() est continue sur
est continue sur ![]() , strictement croissante car
, strictement croissante car ![]() .
.
![]() ,
,![]()
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
Elle admet une fonction réciproque ![]() strictement croissante et définie sur
strictement croissante et définie sur ![]() .
.
Exercice 3 (suite)
Question 2
Montrer que ![]() est dérivable sur
est dérivable sur ![]() et exprimer
et exprimer ![]() en fonction de
en fonction de ![]() .
.
Correction : On a vu que ![]() est dérivable sur
est dérivable sur ![]() et que
et que ![]()
Par théorème, ![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
On remarque que ![]() , donc
, donc ![]() .
.
![]() .
.
Exercice 3 (fin)
Question 3
Montrer que ![]() est deux fois dérivable sur
est deux fois dérivable sur ![]() , exprimer
, exprimer ![]() en fonction de
en fonction de ![]() et donner la valeur de
et donner la valeur de ![]() .
.
Correction : On utilise :
![]() .
.
Alors ![]() est dérivable et
est dérivable et
![]()
en remplaçant ![]() en fonction de
en fonction de ![]() ,
,
![]() .
.
donc ![]()
![]() .
.
Exercice 4
Question 1
Soit ![]() . Démontrer que la fonction
. Démontrer que la fonction ![]()
est une bijection de ![]() sur
sur ![]() .
.
Exercice 4 (fin)
Question 2
Déterminer la fonction réciproque de ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Fonction bornée
On définit si ![]() ,
, ![]()
Question 1
![]() est bornée. Vrai ou Faux ?
est bornée. Vrai ou Faux ?
Correction : Si ![]() donc
donc ![]()
On a donc prouvé que ![]() est bornée.
est bornée.
Question 2
Déterminer ![]() .
.
Correction :
Question 3
Déterminer ![]() .
.
Correction : ![]() En utilisant si
En utilisant si ![]()
![]() ,
, ![]() .
.
![]() En remarquant que
En remarquant que ![]() ,
, ![]() .
.
Par double inégalité, ![]() .
.
On a de plus démontré que ![]() est le minimum de
est le minimum de ![]() . Il est obtenu en tous les points
. Il est obtenu en tous les points ![]() .
.
4. Équation fonctionnelle
Exercice 1
Trouver toutes les bijections ![]() de
de ![]() sur lui-même telles que
sur lui-même telles que
![]() .
.
Correction : ![]() Comme
Comme ![]() existe, on obtient
existe, on obtient ![]() .
.
![]() Soit
Soit ![]() , on note
, on note ![]() et
et ![]() .
.
Si ![]() ,
, ![]() soit
soit ![]() soit :
soit :
![]()
Si ![]() ,
, ![]() , donc
, donc ![]() est constante égale à
est constante égale à ![]() .
.
![]() est une suite arithmétique de raison
est une suite arithmétique de raison ![]() .
.
Si ![]() ,
, ![]() vérifie
vérifie ![]() ce qui contredit le fait que
ce qui contredit le fait que ![]() est une suite de
est une suite de ![]() donc une suite bornée.
donc une suite bornée.
Alors ![]() et
et ![]() est une suite constante, donc
est une suite constante, donc ![]() soit
soit ![]() .
.
On a donc prouvé que ![]()
![]() Réciproquement
Réciproquement ![]() est solution du problème.
est solution du problème.
Le problème admet une seule solution ![]() .
.
Exercice 2
Le but de l’exercice est d’étudier les fonctions ![]() telles que
telles que
![]()
Question 1
Si ![]() est solution du problème proposé,
est solution du problème proposé,
( ![]() et
et ![]() ) ou (
) ou (![]() et
et ![]() ). Vrai ou Faux ?
). Vrai ou Faux ?
Correction : Soit ![]() de
de ![]() dans
dans ![]() telle que
telle que ![]() .
.
En prenant ![]() et
et ![]() ,
,
![]() , donc
, donc ![]()
et comme ![]() ,
, ![]() .
.
Par double inégalité ![]()
donc ![]() ou
ou ![]()
ce qui donne :
![]()
ou ![]()
![]() (
(![]() et
et ![]() )
)
ou (![]() et
et ![]() ).
).
Question 2
Nombre de solutions vérifiant de plus ![]() .
.
Correction : On suppose ![]() , alors
, alors ![]() .
.
Pour tout ![]()
donne ![]() .
.
Puis ![]()
soit ![]()
![]()
Par double inégalité, ![]() .
.
On a prouvé que ![]()
Si ![]() ,
, ![]() .
.
Il est évident que ![]() vérifie la condition et
vérifie la condition et ![]() .
.
Question 3
Nombre de solutions du problème proposé ?
Correction : On suppose que ![]() .
.
On note ![]() .
.
![]() vérifie
vérifie ![]() ,
,
![]()
avec ![]() , donc
, donc ![]() et pour tout
et pour tout ![]()
Le problème a au plus deux solutions : ![]() et
et ![]() .
.
Il est évident que ces deux fonctions sont solutions.
Le problème a exactement deux solutions.
Exercice 3
Soit ![]() non nulle de
non nulle de ![]() dans
dans ![]() telle que
telle que ![]()
![]() et
et ![]() .
.
Question 1
![]() pour tout
pour tout ![]()
Question 2
Pour tout rationnel ![]() ,
, ![]() .
.
Question 3
![]() est croissante.
est croissante.
Question 4
Le nombre de solutions du problème
5. Avec la partie entière
Exercice 1
Si ![]() et
et ![]() ,
,
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() Première méthode
Première méthode
On écrit ![]() avec
avec ![]() et
et ![]() , donc
, donc ![]() où
où ![]() .
.
On peut écrire ![]() avec
avec ![]() et
et ![]() et
et ![]()
![]() , donc
, donc ![]()
![]() avec
avec ![]()
donc ![]() .
.
![]() Deuxième méthode
Deuxième méthode
Soit ![]() .
.
![]() On calcule
On calcule ![]() :
:
![]() car
car ![]()
donc ![]() ,
,
et ![]() ,
,
![]()
soit ![]()
![]() est 1-périodique.
est 1-périodique.
![]() On suppose que
On suppose que ![]() .
.
![]() et
et ![]() car
car ![]()
![]()
![]() .
.
![]()
![]() si
si ![]() et
et ![]() est une fonction 1-périodique donc
est une fonction 1-périodique donc ![]() .
.
Exercice 2
Soit ![]() . Pour tout réel
. Pour tout réel ![]() ,
,
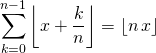 . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : On note 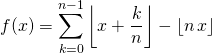 .
.
![]() Périodicité de
Périodicité de ![]() :
:
![]()
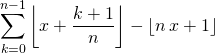
en posant ![]() ,
,
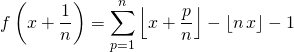
Compte tenu de la valeur supplémentai- re ![]() et de la valeur
et de la valeur ![]() absente :
absente :
![]()
![]() .
.
![]() est
est ![]() – périodique.
– périodique.
![]() Si
Si ![]() ,
, ![]() , donc
, donc ![]() .
.
Pour tout ![]() ,
, ![]()
donc ![]()
et ![]() .
.
![]() Par
Par ![]() – périodicité,
– périodicité, ![]() est nulle sur
est nulle sur ![]() .
.
Exercice 3
Résoudre si ![]() est réel :
est réel : ![]()
![]()
Correction : ![]() Transformation de la relation
Transformation de la relation
Comme ![]() est une somme et différence de parties entières, c’est un entier, donc
est une somme et différence de parties entières, c’est un entier, donc ![]() avec
avec ![]()
alors ![]()
donc ![]()
et l’équation s’écrit ![]()
où ![]() est un entier impair.
est un entier impair.
![]() Analyse
Analyse
On définit sur ![]() ,
, ![]() .
.
![]()
![]()
![]()
![]() .
.
![]() Synthèse
Synthèse
On cherche les entiers impairs ![]() tels que
tels que ![]()
![]()
![]() ,
, ![]() ,
, ![]() .
.
![]() Si
Si ![]() , pour tout
, pour tout ![]() ,
,
![]() .
.
Les trois suites ![]() sont des suites arithmétiques de terme initial nul et de raison
sont des suites arithmétiques de terme initial nul et de raison ![]() donc si
donc si ![]() ,
,
![]() .
.
![]()
![]()
si ![]() , pour tout
, pour tout ![]() ,
,
![]() .
.
Les trois suites ![]() sont des suites arithmétiques de terme initial nul et de raison égale à
sont des suites arithmétiques de terme initial nul et de raison égale à ![]() , donc
, donc ![]() .
.
![]()
![]() ssi
ssi ![]() , mais seul l’entier impair
, mais seul l’entier impair ![]() convient.
convient.
Le problème admet une seule solution : ![]() .
.
6. Calculs de dérivées de fonctions en maths sup
Pour chaque question, on cherchera le domaine de dérivabilité et la dérivée.
Question 1
![]() .
.
Question 2
![]() .
.
Question 3
![]() .
.
Question 4
![]() .
.
Question 5
![]()
Question 6
![]() .
.
Question 7
![]()
Question 8
![]() .
.
Question 9
![]() .
.
Question 10
Soit ![]() ,
, ![]() .
.
Question 11
![]() .
.
Question 12
![]()
Question 13
![]()
Question 14
![]() .
.
Question 15
![]() .
.
Question 16
![]() .
.
Faites la différence en cours de maths, grâce aux méthodes et aux conseils de nos cours en ligne de Maths pour les taupins en Maths Sup :

