Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Les matrices : exercices et corrigés de Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Pour réussir en Maths Sup, il est important d’adopter les bonnes méthodes de travail dès les premiers mois de prépa. Bien connaître les chapitres de maths au programme de Maths Sup est indispensable pour réussir sa 2eme année de Maths Spé, et pour évidemment réussir avec brio les concours post-prépa.
Exercice sur les écritures de matrices et opérations de Maths Sup
Déterminer la matrice dans les bases canoniques de ![]() où
où ![]()
![]() .
.
Exercice sur le calcul de l’inverse d’une matrice en Maths Sup
Montrer que 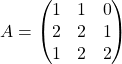 est une matrice inversible et calculer son inverse en l’interprétant comme une matrice de changement de bases.
est une matrice inversible et calculer son inverse en l’interprétant comme une matrice de changement de bases.
Exercice sur l’interprétation de matrices d’ordre 
Soit ![]() ,
, ![]() et
et ![]() telle que
telle que
![]() ,
, ![]() si
si ![]() et
et ![]() si
si ![]() .
.
Question :
Calculer si ![]() ,
, ![]() .
.
Exercice sur le produit de matrices d’ordre  en Maths Sup
en Maths Sup
Soient ![]() et
et ![]() et
et ![]() .
.
On définit les matrices ![]() par
par ![]()
![]() et
et ![]()
avec ![]() ,
,
![]() et
et ![]() .
.
Question :
Calculer ![]() .
.
Exercice sur l’utilisation de la base canonique en Maths Sup
Démontrer que pour toute application linéaire ![]() de
de ![]() dans
dans ![]() il existe une unique matrice
il existe une unique matrice ![]() telle que
telle que
![]() ,
, ![]() .
.
Exercice sur les matrices de rang  et généralisation en Maths Sup
et généralisation en Maths Sup
Soit ![]() de rang
de rang ![]() .
.
![]() est la somme de
est la somme de ![]() matrices de rang 1 .
matrices de rang 1 .
Vrai ou faux ?
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Correction d’exercice sur les écritures de matrices et opérations
On démontre facilement que ![]() est une application linéaire de
est une application linéaire de ![]() dans
dans ![]() .
.
Sa matrice est de type ![]() .
.
On détermine l’image de la base canonique de ![]() .
.
![]()
![]()
![]()
![]()
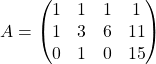 .
.
Correction d’exercice sur le calcul de l’inverse d’une matrice
Si ![]() est une base de
est une base de ![]() , on introduit
, on introduit ![]() ,
, ![]() et
et ![]() .
.
Il est immédiat que ![]() , puis
, puis ![]() et enfin
et enfin
![]()
![]()
![]() .
.
La famille ![]() est une famille génératrice de
est une famille génératrice de ![]() , de cardinal égal à
, de cardinal égal à ![]() , c’est une base de
, c’est une base de ![]() et
et ![]() est la matrice de passage de
est la matrice de passage de ![]() à
à ![]() , donc
, donc ![]() est inversible et
est inversible et ![]() est la matrice de passage de la base
est la matrice de passage de la base ![]() à la base
à la base ![]()
soit
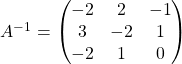 .
.
Correction d’exercice sur l’interprétation de matrices d’ordre 
![]() est la matrice de
est la matrice de ![]() dans la base canonique de
dans la base canonique de ![]() .
.
Il est évident que ![]()
ce qui se traduit par ![]() .
.
Correction d’exercice sur le produit de matrices d’ordre 
On note ![]() .
.
![]() ,
,
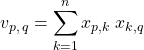
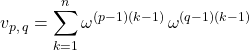
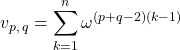
Avec ![]() ,
, 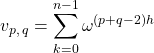
Si ![]() , on doit calculer
, on doit calculer
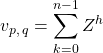 .
.
![]() Si
Si ![]() ,
, ![]()
![]() Si
Si ![]() ,
, ![]()
or ![]() , et donc
, et donc ![]() .
.
On discute maintenant l’équation ![]() ssi
ssi ![]() ssi
ssi ![]() ssi
ssi ![]()
ssi ![]()
Comme ![]() ,
,![]() ,
,
![]() est un multiple de
est un multiple de ![]()
ssi ![]() ou
ou ![]()
ssi ![]() ou
ou ![]() .
.
On en déduit que ![]() ,
, ![]() si
si ![]() , les autres termes sont nuls.
, les autres termes sont nuls.
Pour ![]() on obtient :
on obtient :
 .
.
Correction de l’exercice sur l’utilisation de la base canonique
On raisonne par analyse-synthèse.
Soit ![]() une application linéaire
une application linéaire ![]() de
de ![]() dans
dans ![]()
Analyse : On suppose qu’il existe ![]() telle que
telle que
![]() ,
, ![]()
On note ![]() .
.
En refaisant les calculs du § 3.4. de l’aide mémoire, on démontre que
![]() ,
, ![]()
donc ![]()
Le problème a donc au plus une solution ![]() telle que
telle que
![]() ,
, ![]()
Synthèse :
On définit la matrice ![]()
par ![]()
Grâce au calcul de la partie analyse,
![]() ,
, ![]()
On prouve facilement que l’application ![]() est linéaire.
est linéaire.
Les applications linéaires ![]() et
et ![]() sont égales sur la base canonique de
sont égales sur la base canonique de ![]() elles sont donc égales.
elles sont donc égales.
Conclusion : pour toute application linéaire ![]() de
de ![]() dans
dans ![]() , il existe une unique matrice
, il existe une unique matrice ![]() telle que
telle que
![]() ,
, ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction d’exercice sur les matrices de rang  et généralisation
et généralisation
Vrai
On sait que ![]() est équivalente à la matrice de type
est équivalente à la matrice de type ![]() notée
notée ![]() .
.
Il existe ![]() et
et ![]() telles que
telles que ![]() .
.
En introduisant la base canonique ![]() de
de ![]() ,
,
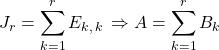 avec
avec ![]() .
.
![]() est une matrice de rang
est une matrice de rang ![]() , la multiplication par une matrice inversible ne change pas le rang d’une matrice, donc
, la multiplication par une matrice inversible ne change pas le rang d’une matrice, donc ![]() .
.
Pour intensifier ses révisions et ses entraînements il est possible de se tester sur les exercices de cours en ligne de MPSI, PTSI et PCSI. Les difficultés comme les points forts se feront rapidement connaître. Quelques idées de chapitres à travailler :

