Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les primitives et intégrales en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : IPP, Intégrale de Wallis
1. Avec seulement un peu de réflexion
2. Par intégration par parties
3. Par changement de variable.
4. En utilisant les deux théorèmes
5. Fonctions paires, impaires, périodiques
6. Calcul d’intégrales sur un segment
7. Intégrales de Wallis (Première partie)
8. Une famille d’intégrales dépendant de 2 paramètres
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Avec un peu de réflexion des primitives simples
Question 1
Primitives de ![]()
Correction :
Donc les primitives de
Question 2
Si ![]() , primitives de
, primitives de ![]()
Correction :
On se place sur ![]() .
.
On remarque que ![]() avec
avec ![]() .
.
Primitives : ![]() .
.
Question 3
Primitives de ![]()
Correction : On se place sur ![]() ou sur
ou sur ![]() .
.
On remarque que ![]() avec
avec ![]() .
.
Primitives : ![]() .
.
Question 4
Soit ![]() . Primitives de
. Primitives de ![]() .
.
Correction : On se place sur ![]() pour avoir
pour avoir ![]() .
.
![]() avec
avec ![]() .
.
![]() Si
Si ![]() ,
,
primitives : ![]() .
.
![]() Si
Si ![]() ,
,
primitives : ![]() .
.
Question 5
Si ![]() , primitives de
, primitives de ![]()
Correction : On se place sur ![]() et on écrit
et on écrit ![]()
Primitives : ![]() .
.
Question 6
Si ![]() et
et ![]() , primitives de
, primitives de ![]()
Correction : ![]()
Primitives : ![]() .
.
Question 7
Primitives de
![]() et
et ![]() .
.
Question 8
Primitives de
![]() et
et ![]() .
.
Question 9
Primitives de ![]() .
.
Question 10
Primitives de ![]() .
.
Question 11
Primitives de ![]() .
.
Question 12
Primitives de ![]() .
.
Question 13
Primitives de ![]() .
.
Question 14
Primitives de ![]() où
où ![]() .
.
Question 15
Primitives de ![]()
Question 17
Soit ![]() . Primitives de
. Primitives de ![]() .
.
Correction : On se place sur ![]() ou
ou ![]() ou
ou ![]() .
.
On cherche ![]() et
et ![]() réels tels que si
réels tels que si ![]() ,
,
![]()
![]()
On obtient les CNS
![]()
![]()
![]()
![]()
Les primitives sont les fonctions :
![]() .
.
Question 18
Primitives de ![]() .
.
Correction : Le dénominateur n’a pas de racine réelle, on l’écrit comme somme de deux carrés.
![]()
Puis 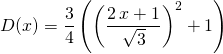 .
.
![]() avec
avec ![]() .
.
Une primitive ![]() est définie par
est définie par
![]() .
.
Ls primitives s’écrivent :
![]() .
.
Question 19
Primitives de ![]() .
.
Correction : ![]() est continue sur
est continue sur ![]() .
.
Le dénominateur n’a pas de racine réelle. On l’écrit comme somme de deux carrés.
![]()
![]()
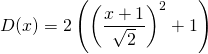
![]() avec
avec ![]()
![]() est une primitive de
est une primitive de ![]() .
.
Question 20
Primitives de ![]()
Correction: On remarque que ![]() avec
avec ![]() .
.
Les primitives sont les fonctions définies sur ![]() par
par ![]()
Question 21
Primitives de ![]()
Question 22
Primitives de ![]()
2. Par intégration par parties
Question 1
Primitives de ![]() .
.
Correction : On se place sur ![]() .
.
Soit si ![]() ,
,
![]()
![]() et
et ![]() sont des fonctions classe
sont des fonctions classe ![]() sur
sur ![]() .
.
![]()
![]() et
et ![]()
Par intégration par parties,
![]()
![]()
![]() est une primitive de
est une primitive de ![]() sur
sur ![]() .
.
Remarque : On peut prolonger ![]() par continuité en
par continuité en ![]() par
par ![]() et
et ![]() .
.
![]() est continue sur
est continue sur ![]() ,
, ![]() admet une limite égale à
admet une limite égale à ![]() en 1 (resp.
en 1 (resp. ![]() en
en ![]() )
)
Alors ![]() est dérivable en
est dérivable en ![]() et
et ![]() ,
, ![]() .
.
Donc ![]() est une primitive de
est une primitive de ![]() sur
sur ![]() .
.
Question 2
Primitives de ![]() .
.
Correction : On se place sur ![]() où
où ![]() .
.
Soit ![]() et
et ![]() .
.
Les fonctions ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() .
.
![]()
![]() et
et ![]()
Par intégration par parties,
![]() .
.
![]()
![]() est une primitive de
est une primitive de ![]() sur
sur ![]() .
.
Question 3
Primitives de ![]() .
.
Correction : Plutôt que de faire deux intégrations par parties, il vaut mieux chercher une primitive sous la forme ![]() .
.
![]()
![]()
![]()
![]() ssi
ssi
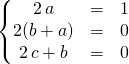
ssi ![]() .
.
![]() est une primitive de
est une primitive de ![]() .
.
Question 4
Primitives de ![]() .
.
Correction : ![]() Utilisation de l’indication
Utilisation de l’indication
Si ![]() ,
, ![]() est dérivable sur
est dérivable sur ![]() car
car ![]() donc
donc ![]() .
.
![]()
![]() .
.
![]() On cherche une primitive sur
On cherche une primitive sur ![]()
Soit si ![]() ,
, ![]() .
.
![]() et
et ![]() sont des fonctions de classe
sont des fonctions de classe ![]() sur
sur ![]() .
.
![]()
![]() et
et ![]()
Par intégration par parties,
![]()
On écrit ![]()
![]()
![]()
On utilise l’indication
![]()
![]()
![]()
Une primitive est
![]()
Question 5
Primitives de ![]() .
.
3. Changement de variable
Les changements de variables sont donnés dans l’indication. Vous pouvez ainsi essayer de le deviner avant de consulter l’indication.
Question 1
Primitives de ![]() .
.
Correction : On définit si ![]() ,
,
![]() .
.
![]() .
.
Après multiplication du numérateur et dénominateur par ![]() :
:
![]() .
.
![]() .
.
En notant ![]() , on a écrit
, on a écrit
![]()
![]()
![]() est une primitive de
est une primitive de ![]() .
.
Question 2
Primitives de ![]() .
.
Correction :
On cherche une primitive sur ![]() et on écrit
et on écrit ![]() .
.
Soit ![]() un réel.
un réel.
![]()
s’écrit si l’on note ![]()
![]()
![]()
On cherche deux réels ![]() et
et ![]() tels que
tels que
![]()
ce qui donne les deux équations
![]() et
et ![]()
![]()
![]() et
et ![]() .
.
![]()
![]()
On remarque que ![]() .
.
![]() est une primitive de
est une primitive de ![]() .
.
Question 3
Primitives de ![]() .
.
Correction : On cherche une primitive sur ![]()
![]()
On note ![]() , on remarque que
, on remarque que
![]() .
.
donc ![]()
En écrivant ![]() , on peut écrire puis simplifier les fractions :
, on peut écrire puis simplifier les fractions :
![]()
et obtenir :
![]()
![Rendered by QuickLaTeX.com F(x) = \displaystyle \left [ \ln \frac t {1 + t} \right ] _1 ^{\textrm{ch } x}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e3d6c9570b4db456bfb1b9312218a2ae_l3.png) .
.
![]() est une primitive de
est une primitive de ![]() .
.
Question 4
Primitives de ![]() .
.
Question 5
Primitives de ![]() .
.
Question 6
Primitives de ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Et avec les deux théorèmes
Question 1
Primitives de ![]() .
.
Correction : On se place sur ![]() .
.
Si ![]() ,
, ![]()
![]() et
et ![]() sont des fonctions de classe
sont des fonctions de classe ![]() sur
sur ![]() .
.
![]()
![]() et
et ![]()
Par intégration par parties,
![]()
![]()
On utilise maintenant un changement de variable pour calculer ![]()
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() (
(![]() )
)
Si ![]() ,
, ![]() et si
et si ![]() ,
, ![]() .
.
![]()
![]()
![]()
![Rendered by QuickLaTeX.com G(x) = \displaystyle \left [ \frac {u ^2} 2 - u + \ln(1 + u) \right] _0 ^{\sqrt{x}}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-9c67f7c14abc5b04b7b1e5ae11d05aa1_l3.png)
Une primitive de ![]() sur
sur ![]() est
est
![]() .
.
Question 2
Primitives de ![]() .
.
Correction : On se place sur ![]() .
.
Si ![]() ,
, ![]()
![]() La fonction
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() (et
(et ![]() ).
).
Si ![]() ,
, ![]() et si
et si ![]() ,
, ![]() .
.
Par changement de variable
![]()
![]()
![]()
![]() et
et ![]() sont des fonctions de classe
sont des fonctions de classe ![]() sur
sur ![]() .
.
![]()
![]() et
et ![]()
Par intégration par parties,
![]()
![]()
En utilisant ![]() ,
, ![]() est égal à :
est égal à :
![]()
![]()
est une primitive de ![]()
soit aussi
![]()
5. Fonctions paires, impaires, périodiques
Question 1
Toute primitive d’une fonction définie sur ![]() et périodique de période
et périodique de période ![]() est périodique de période
est périodique de période ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() est périodique de période
est périodique de période ![]() et
et ![]() est une primitive de
est une primitive de ![]() qui n’est pas périodique.
qui n’est pas périodique.
Question 2.
Si ![]() est définie sur
est définie sur ![]() et
et ![]() -périodique, si
-périodique, si ![]() est une primitive de
est une primitive de ![]() telle que
telle que ![]() ,
, ![]() est
est ![]() -périodique
-périodique
Vrai ou Faux ?
Correction : On note ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et
et ![]()
![]() .
.
Donc ![]() est constante et comme
est constante et comme ![]() ,
, ![]() est nulle, ce qui donne :
est nulle, ce qui donne : ![]() est
est ![]() – périodique.
– périodique.
Question 3
Toute primitive d’une fonction continue sur ![]() et paire est impaire. Vrai ou Faux ?
et paire est impaire. Vrai ou Faux ?
Correction : La fonction ![]() est paire,
est paire, ![]() est une primitive de
est une primitive de ![]() qui n’est pas impaire.
qui n’est pas impaire.
Question 4
La primitive nulle en 0 d’une fonction continue paire sur ![]() est impaire. Vrai ou Faux ?
est impaire. Vrai ou Faux ?
Correction :
Soit ![]() une fonction continue sur
une fonction continue sur ![]() et
et ![]() la primitive de
la primitive de ![]() vérifiant
vérifiant ![]() .
.
On note pour ![]() ,
, ![]() .
.
![]() est dérivable et pour tout réel
est dérivable et pour tout réel ![]() ,
,
![]()
![]()
![]() .
.
![]() est une fonction constante sur
est une fonction constante sur ![]() avec
avec ![]() , donc
, donc ![]() ce qui prouve que
ce qui prouve que ![]() est impaire.
est impaire.
Question 5
Toute primitive d’une fonction définie sur ![]() et impaire est paire.
et impaire est paire.
Exercice 1
Si ![]() est continue sur
est continue sur ![]() à valeurs dans
à valeurs dans ![]()
![]() si
si ![]() est paire,
est paire, ![]()
![]() si
si ![]() est impaire,
est impaire, ![]() .
.
Exercice 2
Si ![]() est continue sur
est continue sur ![]() à valeurs dans
à valeurs dans ![]() et périodique de période
et périodique de période ![]() .
.
Pour tout ![]() ,
,
![]()
![]()
![]()
![]() .
.
6. Calcul d’intégrales
Pour chaque question, on cherchera le domaine de dérivabilité et la dérivée.
Exercice 1
Calculer ![]() .
.
Correction : ![]() et
et ![]() sont des fonctions de classe
sont des fonctions de classe ![]() sur
sur ![]() .
.
![]()
![]() et
et ![]()
Par intégration par parties,
![]()
![]()
et en utilisant une primitive classique :
![]()
![]()
![]() .
.
Exercice 2
Calculer ![]()
Correction : ![]()
La fonction ![]() est une fonction de classe
est une fonction de classe ![]() sur
sur ![]() .
.
![]()
Par le théorème de changement de variable, ![]()
![]() est égal à
est égal à
![]()
![]() (2)
(2)
En additionnant (1) et (2) :
![]()
donc ![]()
alors ![]() .
.
Exercice 3
Calculer ![]() où
où ![]() et
et ![]() sont entiers.
sont entiers.
Correction : On note ![]()
avec un peu de trigonométrie en maths sup :
![]()
![]()
Puis si ![]()
![]()
et ![]() .
.
![]() si
si ![]() ,
, ![]() .
.
![]() si
si ![]() ,
,
![]() .
.
![]() si
si ![]() ,
, ![]() et
et ![]() donc
donc ![]() .
.
Exercice 4
Calculer ![]() .
.
Correction : ![]() est de classe
est de classe ![]() sur
sur ![]() à valeurs dans
à valeurs dans ![]() .
.
![]()
Par le théorème de changement de variable, ![]() .
.
![]()
![]() .
.
![]() est une primitive de
est une primitive de ![]() .
.
![]()
et ![]() est une primitive de
est une primitive de ![]()
![]() .
.
On termine avec ![]()
Réponse : ![]() .
.
Exercice 5
Calculer : ![]() .
.
Correction : ![]() est une fonction de classe
est une fonction de classe ![]() et
et
![]()
Par le théorème de changement de variable, ![]() .
.
![]()
![]() sur le segment d’intégration.
sur le segment d’intégration.
![]()
![]()
![Rendered by QuickLaTeX.com I = \displaystyle \left [ - \cos(u) + \frac 1 3 \cos ^3(u) \right ] _ 0 ^{\pi/6}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e4abf6785170e2ca469179f1748559ed_l3.png)
![]()
![]() .
.
Exercice 6
Si ![]() , justifier l’existence de
, justifier l’existence de ![]() .
.
Calculer ![]() .
.
Correction : Soit ![]() .
.
Soit ![]() ,
, ![]() ,
, ![]() est une fonction continue sur
est une fonction continue sur ![]() ce qui justifie l’existence de
ce qui justifie l’existence de ![]() .
.
On note ![]() la primitive de
la primitive de ![]() s’annulant en 1.
s’annulant en 1.
Alors si ![]()
![]()
Comme ![]() est continue en
est continue en ![]() , alors
, alors ![]() .
.
Il n’est pas possible d’intégrer par parties sur ![]() en prenant pour l’une des fonctions la fonction
en prenant pour l’une des fonctions la fonction ![]() , mais on peut intégrer par parties sur
, mais on peut intégrer par parties sur ![]() .
.
On définit
![]() et
et ![]() ,
,
ces fonctions étant de classe ![]() sur
sur ![]() , on peut donc intégrer par parties :
, on peut donc intégrer par parties :
![]()
![]()
![]()
![]()
Si ![]() tend vers
tend vers ![]() , on obtient à la limite la valeur de
, on obtient à la limite la valeur de ![]() :
: ![]() .
.
Exercice 7
Trouver ![]() tel que :
tel que : ![]() .
.
Exercice 8
Question 1
Soit ![]() une fonction continue sur
une fonction continue sur ![]() à valeurs réelles telle que
à valeurs réelles telle que
![]() .
.
![]()
Question 2
Calculer ![]() .
.
7. Intégrales de Wallis (le début)
Question 1
Soit si ![]() ,
, ![]() , alors
, alors ![]() .
.
Vrai ou Faux ?
Correction : En utilisant le changement de variable ![]() , de classe
, de classe ![]() sur
sur ![]() ,
,
![]() soit
soit ![]() .
.
Question 2
![]()
Correction : En utilisant le changement de variable ![]() , de classe
, de classe ![]() sur
sur ![]() ,
,
![]()
![]()
![]() .
.
On termine par la relation de Chasles :
![]()
![]()
![]() .
.
Question 3
![]()
Correction : En intégrant ![]() par parties avec les fonctions de classe
par parties avec les fonctions de classe ![]() sur
sur ![]() :
:
![]() et
et ![]() ,
,
![]()
![]() et
et ![]()
![]()
![]() .
.
En utilisant ![]() , on obtient par linéarité de l’intégrale
, on obtient par linéarité de l’intégrale ![]()
donc ![]() .
.
Question 4
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : Soit pour ![]()
![]()
![]() .
.
La suite ![]() est constante, donc
est constante, donc ![]() .
.
Question 5.
![]() .
.
Question 6.
Valeur de ![]() .
.
8. Une famille d’intégrales dépendant de deux paramètres
Si ![]() , on définit
, on définit
![]() .
.
Question 1
Si ![]() et
et ![]() , exprimer
, exprimer ![]() en fonction de
en fonction de ![]() .
.
Correction : On utilise une intégration par parties avec ![]() et
et ![]() qui sont de classe
qui sont de classe ![]() sur
sur ![]() .
.
![]()
![]() et
et ![]()
![]()
![]()
donc ![]() .
.
Question 2
Calculer ![]() pour
pour ![]() .
.
Correction : On note si ![]() ,
, ![]()
et on raisonne par récurrence.
![]()
![]()
![]()
![]() .
.
Donc ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
On utilise la formule de la question 1 en replaçant ![]() par
par ![]() .
.
![]()
![]()
puis avec ![]() :
:
![]()
![]()
ce qui prouve ![]() .
.
La propriété a été démontrée par récurrence.
En particulier, ![]() .
.
Question 3
Si ![]() et
et ![]() , calculer
, calculer
![]() .
.
Correction :
![]() Recherche : On cherche un changement de variable de la forme
Recherche : On cherche un changement de variable de la forme ![]() tel que
tel que
![]() et
et ![]() .
.
On résout donc le système
![]() ssi
ssi ![]()
On a donc obtenu ![]() .
.
![]() Rédaction
Rédaction
![]()
![]() est de classe
est de classe ![]() et
et
![]()
donne par le théorème de changement de variable :
![]()
![]() et
et ![]()
![]()
![]()
![]()
![]() .
.
Question 4
Soit ![]() . Calculer
. Calculer
![]()
Correction : La fonction ![]() est une bijection de classe
est une bijection de classe ![]() .
.
Par le théorème de changement de variable
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
donc ![]() .
.
Question 5
Soit ![]() .
.
En déduire la valeur de ![]()
Correction : ![]()
![]()
en utilisant le changement de variable ![]() ,
, ![]()
![]()
Puis par le changement de variable ![]() :
:
![]()
![]()
![]()
et par la relation de Chasles :
![]()
donc ![]()
![]() .
.
Question 6
Si ![]() , calculer
, calculer 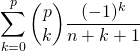 .
.
Correction : Si ![]() ,
, ![]()
![]() .
.
Par le binôme de Newton :
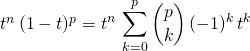
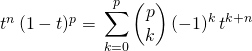 .
.
Par linéarité de l’intégrale :
![Rendered by QuickLaTeX.com \displaystyle I(n , p) = \sum _ {k = 0} ^p \binom p k \left [ \frac {( - 1) ^k \, t ^{n + k + 1} } {n + k + 1} \; \; \; \right] _ 0 ^1.](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-56dc13049ea639f13cb987e8279075bf_l3.png)
soit 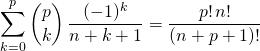
N’hésitez pas à utiliser les autres cours en ligne de maths au programme de Maths Sup, pour vous aider et vous guider dans vos révisions personnelles :

