Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices et corrigés sur les systèmes en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices de systèmes
1. Système de 2 équations à 2 inconnues
2. Système de ![]() équations à
équations à ![]() inconnues
inconnues
3. Système de ![]() équations à
équations à ![]() inconnues et
inconnues et ![]() paramètres
paramètres
4. Système de ![]() équations à
équations à ![]() inconnues et
inconnues et ![]() paramètres
paramètres
5. Système de 3 équations à ![]() inconnues
inconnues
6. ![]() équations à
équations à ![]() inconnues et un paramètre
inconnues et un paramètre
7. ![]() équations à
équations à ![]() inconnues et
inconnues et ![]() paramètres
paramètres
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Système de 2 équations à 2 inconnues
Exercice 1
Le système ![]() :
: ![]() a une unique solution ssi
a une unique solution ssi ![]() .
.
Exprimer la solution lorsque le système admet une unique solution. Vrai ou Faux ?
Correction :
![]() Si
Si ![]() , en formant
, en formant ![]()
![]() :
: ![]()
avec ![]() ,
,
![]() :
: ![]()
![]() Si
Si ![]() , le système
, le système ![]() est équivalent à un système ayant
est équivalent à un système ayant ![]() ou une infinité de solutions.
ou une infinité de solutions.
![]() Si
Si ![]() et
et ![]() , le système admet une unique solution donnée par
, le système admet une unique solution donnée par ![]() et
et ![]()
![]()
![]()
![]()
![]() .
.
![]() Si
Si ![]() , en échangeant
, en échangeant ![]() et
et ![]()
![]() :
: ![]()
![]() Si
Si ![]() ,
, ![]() et le système
et le système ![]() admet
admet ![]() ou une infinité de solutions.
ou une infinité de solutions.
![]() Si
Si ![]() et
et ![]() ,
, ![]() et le système
et le système ![]() admet
admet ![]() ou une infinité de solutions.
ou une infinité de solutions.
![]() Si
Si ![]() , alors
, alors ![]() , le système admet une unique solution que l’on calcule :
, le système admet une unique solution que l’on calcule :
![]()
![]()
![]() soit
soit ![]() car
car ![]() .
.
![]() Conclusion : le système admet une unique solution ssi
Conclusion : le système admet une unique solution ssi ![]() et dans ce cas
et dans ce cas
![]() et
et ![]() .
.
Exercice 2
On suppose que ![]() .
.
Le système ![]() :
: ![]() a une infinité de solutions ssi
a une infinité de solutions ssi ![]() et
et
![]() et
et ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
Condition nécessaire.
On suppose que le système admet une infinité de solutions.
L’exercice 1 implique que ![]() . On reprend les calculs effectués dans cet exercice.
. On reprend les calculs effectués dans cet exercice.
![]() On suppose que
On suppose que ![]() .
.
![]() On note
On note ![]() tel que
tel que ![]()
alors ![]()
![]()
![]() .
.
Le système est équivalent à
![]()
soit à ![]()
Il admet une infinité de solutions ssi ![]() ce qui donne
ce qui donne ![]() soit
soit ![]() .
.
On a prouvé qu’il existe ![]() tel que
tel que ![]() et
et ![]()
![]() Si
Si ![]() ,
, ![]() .
.
On suppose que ![]() , donc
, donc ![]() .
.
Le système s’écrit : ![]()
ssi ![]() et
et ![]()
![]()
![]() .
.
Comme ![]() , on pose
, on pose ![]() , alors
, alors ![]() ,
, ![]() (c’est
(c’est ![]() ) puis
) puis ![]() et
et ![]() donnent
donnent ![]() .
.
On a prouvé qu’il existe ![]() tel que
tel que
![]() et
et ![]() .
.
Condition suffisante
On suppose qu’il existe ![]() tel que
tel que
![]() et
et ![]() .
.
Le système s’écrit
![]() :
: ![]()
et en formant ![]()
![]() est équivalent à :
est équivalent à : ![]() .
.
![]() admet une infinité de solutions.
admet une infinité de solutions.
2. Système de 4 équations à 4 inconnues
Exercice : Résoudre sur ![]() lorsque
lorsque ![]() ,
,
![]()
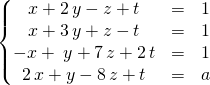
Correction :
![]() On échelonne le système.
On échelonne le système.
![]()
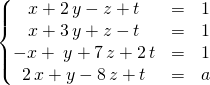
En utilisant ![]() ,
, ![]() ,
, ![]() ,
,
on obtient le système équivalent :
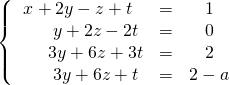
Puis en formant
![]() et
et ![]() ,
,
on obtient le système équivalent :
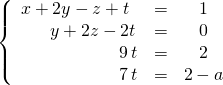
et avec ![]() ,
,
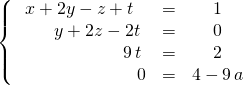
![]() Discussion.
Discussion.
![]() Le système est un système de rang 3, incompatible si
Le système est un système de rang 3, incompatible si ![]() .
.
![]() Si
Si ![]() , on exprime
, on exprime ![]() et
et ![]() en fonction de
en fonction de ![]()
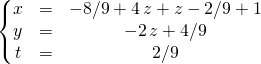
L’ensemble des solutions est donné par
![]() .
.
3. Système de 4 équations à 4 inconnues et 2 paramètres
Exercice : Résoudre sur ![]() lorsque
lorsque ![]() ,
,
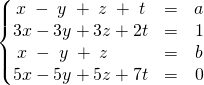
Correction :
![]() On échelonne le système.
On échelonne le système.
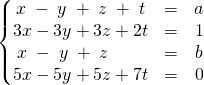
En utilisant ![]() ,
, ![]() ,
, ![]() ,
,
on obtient le système équivalent :
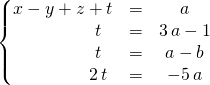
En utilisant
![]() ,
, ![]() ,
,
on obtient le système équivalent :
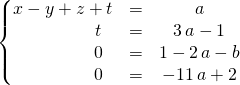
![]() Discussion
Discussion
On obtient un système de rang 2.
Il est compatible ssi ![]()
ssi ![]()
ssi ![]() et
et ![]() .
.
![]() Résolution s’il est compatible
Résolution s’il est compatible
On suppose que ces conditions sont vérifiées, on exprime les solutions en fonction de ![]() et
et ![]() .
.
![]()
ssi ![]()
![]() Conclusion
Conclusion
![]() Si
Si ![]() et
et ![]() , l’ensemble des solutions est donné par
, l’ensemble des solutions est donné par
![]() .
.
![]() Si
Si ![]() ou
ou ![]() , le système n’a pas de solution.
, le système n’a pas de solution.
4. Système de 4 équations à 3 inconnues et 2 paramètres
Exercice : Résoudre sur ![]() lorsque
lorsque ![]() ,
,
![]()
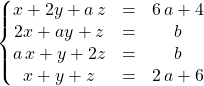
Correction :
![]() On échelonne le système
On échelonne le système
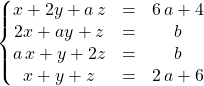
En utilisant ![]() ,
, ![]() ,
, ![]() ,
,
on obtient le système équivalent :
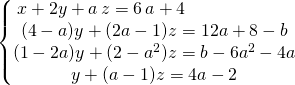
puis en échangeant ![]() et
et ![]()
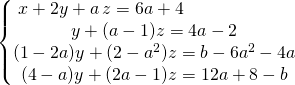
en formant ![]() et
et ![]() , on obtient après calculs le système équivalent :
, on obtient après calculs le système équivalent :
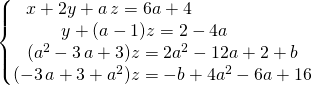
Puis avec ![]()
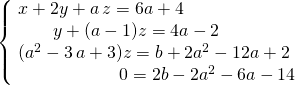
![]() Discussion
Discussion
![]() Le système est incompatible si
Le système est incompatible si ![]()
![]() On suppose que
On suppose que ![]() .
.
Le système est un système de rang 3 car ![]() .
.
et ![]()
ce qui permet de simplifier la dernière équation par ![]()
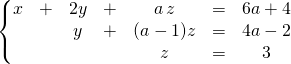
ssi 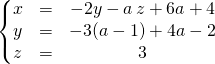
ssi 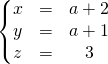
![]() Conclusion
Conclusion
Le système n’a pas de solution si ![]()
et une seule solution ![]() si
si ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
5. Système de 3 équations à 3 inconnues
Exercice : Résoudre sur ![]() lorsque
lorsque ![]() ,
,
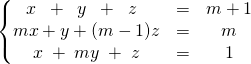
Correction :
![]() On échelonne le système
On échelonne le système
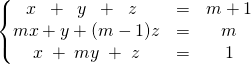
En utilisant ![]() et
et ![]() ,
,
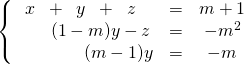
système que l’on réordonne sous la forme pour obtenir un système triangulaire :
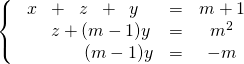
![]() Discussion
Discussion
![]() Si
Si ![]() , le système est incompatible car la dernière équation s’écrit
, le système est incompatible car la dernière équation s’écrit ![]() .
.
Il n’a pas de solution.
![]() Si
Si ![]() , c’est un système de rang 3 admettant une unique solution que l’on obtient en « remontant » le système
, c’est un système de rang 3 admettant une unique solution que l’on obtient en « remontant » le système
![]()
![]()
![]()
![]()
donc la seule solution est ![]()
6. 4 équations à 4 inconnues et un paramètre
Exercice : Résoudre sur ![]() lorsque
lorsque ![]() ,
,
![]()
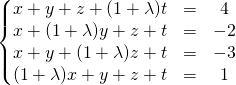
Correction :
![]() On échelonne le système
On échelonne le système
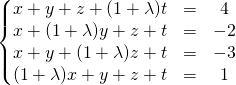
En utilisant ![]() ,
, ![]() et
et ![]() ,
,
on obtient le système équivalent :
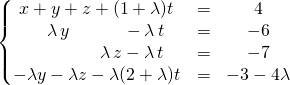
puis avec ![]()
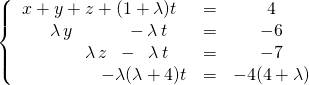
![]() Discussion
Discussion
![]() Si
Si ![]() , le système est de rang 1 et il est incompatble.
, le système est de rang 1 et il est incompatble.
![]() Si
Si ![]() , le système est de rang 3, il est compatible et s’écrit
, le système est de rang 3, il est compatible et s’écrit
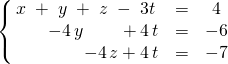
On exprime les solutions en fonction de la variable ![]()
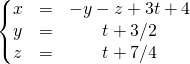
L’ensemble des solutions est l’ensemble
![]() .
.
![]() Si
Si ![]() , le système est de rang 4, il admet une unique solution
, le système est de rang 4, il admet une unique solution
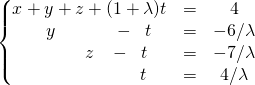
ssi 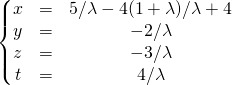
La solution est donnée par ![]() .
.
7. 3 équations à 3 inconnues et 2 paramètres
Exercice : Résoudre sur ![]() lorsque
lorsque ![]() ,
,
![]()
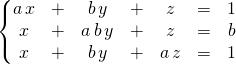
Correction :
![]() On cherche une forme échelonnée.
On cherche une forme échelonnée.
En échangeant la première et la dernière équation :
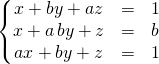
avec les opérations
![]() et
et ![]()
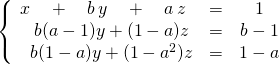
et avec ![]()
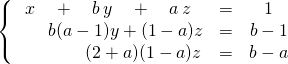
![]() Discussion
Discussion
![]() si
si ![]() , le système est de rang 3, on calcule sa solution en « remontant » les équations :
, le système est de rang 3, on calcule sa solution en « remontant » les équations :
![]()
![]()
![]()
![]()
et ![]()
après calculs, ![]()
La solution est donnée par ![]()
![]()
![]() si
si ![]() , le système s’écrit
, le système s’écrit
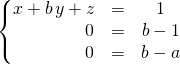
Il admet des solutions ssi ![]()
et dans ce cas les solutions sont les triplets ![]() où
où ![]() .
.
![]() si
si ![]() , le système s’écrit
, le système s’écrit
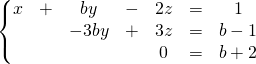
Il admet des solutions ssi ![]() et alors
et alors ![]()
ssi ![]() et
et ![]()
L’ensemble des solutions est l’ensemble des triplets ![]() où
où ![]()
![]() si
si ![]() et
et ![]() , le système s’écrit
, le système s’écrit
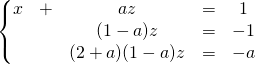
et en formant ![]()
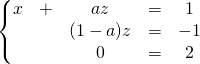
Le système n’a pas de solution.
![]() Conclusion
Conclusion
![]() Le système n’a pas de solution si
Le système n’a pas de solution si
![]() et
et ![]()
ou ![]() et
et ![]()
ou ![]() et
et ![]() .
.
![]() si
si ![]() , il admet une unique solution
, il admet une unique solution
![]()
![]()
![]() si
si ![]() , l’ensemble des solutions est l’ensemble des triplets
, l’ensemble des solutions est l’ensemble des triplets ![]() où
où ![]() .
.
![]() si
si ![]() , l’ensemble des solutions est l’ensemble des triplets
, l’ensemble des solutions est l’ensemble des triplets
![]() où
où ![]() .
.
De nombreux autres exercices et corrigés d’exercices sont également disponibles pour s’entraîner sur le programme de Maths en MPSI, PTSI et PCSI. Anticipez les révisions en travaillant les prochains chapitres du programme :

