Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les variables aléatoires en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Exercice sur la fonction génératrice en Maths Sup
Si ![]() est une variable aléatoire à valeurs dans
est une variable aléatoire à valeurs dans ![]() , on définit pour tout
, on définit pour tout 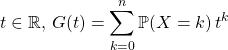 .
.
![]() est appelée fonction génératrice de la variable aléatoire
est appelée fonction génératrice de la variable aléatoire ![]() .
.
Question 1 :
![]() .
.
Vrai ou Faux ?
Question 2 :
Calculer ![]() lorsque
lorsque ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() puis une loi
puis une loi ![]() .
.
Exercice sur l’utilisation de la fonction génératrice en Maths Sup
Soit ![]() , on effectue
, on effectue ![]() tirages sans remise de jetons numérotés de 1 à
tirages sans remise de jetons numérotés de 1 à ![]() .
.
On note ![]() la variable aléatoire égale au nombre de fois où l’on obtient un numéro strictement supérieur aux numéros déjà obtenus.
la variable aléatoire égale au nombre de fois où l’on obtient un numéro strictement supérieur aux numéros déjà obtenus.
Par exemple si ![]() et si l’on obtient
et si l’on obtient ![]() (resp
(resp ![]() ),
), ![]() est égal à 3 (resp. 2).
est égal à 3 (resp. 2).
(le premier numéro tiré donne toujours un maximum).
Question 1 :
Montrer que si ![]() et
et ![]() ,
,
![]()
![]() .
.
Question 2 :
Si ![]() et
et ![]() , on note
, on note 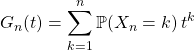 .
.
![]() ,
, ![]() ,
, ![]() .
.
Vrai ou Faux ?
Question 3 :
En déduire la valeur de ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice sur l’ajout d’une boule de couleur opposée en Maths Sup
Une urne contient initialement une boule blanche et une boule noire.
On effectue une succession de tirages dans cette urne. Après chaque tirage, on remet la boule tirée dans l’urne et on ajoute dans l’urne une boule de couleur opposée à celle qui vient d’être tirée.
On effectue en tout ![]() tirages et on suppose qu’il existe un univers probabilisé fini
tirages et on suppose qu’il existe un univers probabilisé fini ![]() associé à cette suite d’épreuves.
associé à cette suite d’épreuves.
Pour tout ![]() , on note
, on note ![]() le nombre de boules blanches présentes dans l’urne juste avant le
le nombre de boules blanches présentes dans l’urne juste avant le ![]() -ème tirage. En particulier, on a
-ème tirage. En particulier, on a ![]() .
.
Question 1 :
Calculer ![]()
Question 2 :
Montrer que ![]() , si
, si ![]() ,
, ![]()
![]() .
.
Question 3 :
À l’aide de la formule précédente, donner la loi de ![]() .
.
![]() ?
?
Exercice sur le tirage de la première et la dernière en Maths Sup
Une urne contient ![]() boules noires et
boules noires et ![]() boules blanches. On fait des tirages sans remise et on note
boules blanches. On fait des tirages sans remise et on note ![]() le rang d’apparition de la première blanche et
le rang d’apparition de la première blanche et ![]() le rang d’apparition de la dernière blanche.
le rang d’apparition de la dernière blanche.
Question 1 :
En déduire la valeur de 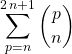 .
.
Question 2 :
![]() .
.
avec ![]() ?
?
Question 3 :
Calculer ![]() .
.
Trouver ![]() tel que
tel que ![]() .
.
![]() ?
?
Exercice sur la loi Hypergéométrique en Maths Sup
On considère une urne contenant ![]() boules dont
boules dont ![]() blanches et
blanches et ![]() boules rouges indiscernables au toucher.
boules rouges indiscernables au toucher.
On effectue ![]() tirages sans remise et on note
tirages sans remise et on note ![]() le nombre de boules blanches tirées.
le nombre de boules blanches tirées.
Question :
Calculer ![]() .
.
Exercice sur le maximum et minimum de 2 tirages en Maths Sup
On effectue 2 tirages avec remise dans un ensemble de jetons numérotés de 1 à ![]() .
.
On appelle ![]() le plus petit numéro obtenu et
le plus petit numéro obtenu et ![]() le plus grand.
le plus grand.
Question 1 :
![]() et
et ![]() suivent la même loi
suivent la même loi
Vrai ou Faux ?
Question 2 :
Calculer l’espérance et la variance de ![]()
Exercice sur deux variables de loi uniforme en Maths Sup
Soit ![]() ,
, ![]() .
.
On tire un numéro ![]() au hasard entre 1 et
au hasard entre 1 et ![]() puis un numéro
puis un numéro ![]() entre 1 et
entre 1 et ![]() .
.
Question 1 :
Calculer ![]() .
.
Question 2 :
![]() a même loi que
a même loi que ![]() .
.
Vrai ou Faux ?
Correction de l’exercice sur la fonction génératrice en Maths Sup
Question 1 :
Vrai
On dérive la fonction polynôme ![]() ,
,
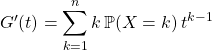 .
.
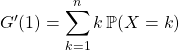
On ajoute un terme nul, 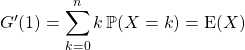 .
.
Question 2 :
![]() Lorsque
Lorsque ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() ,
,
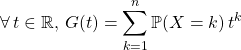
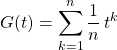 .
.
![]()
![]() ,
, 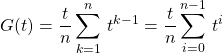
![]() .
.
![]() Si
Si ![]() , on note
, on note ![]() .
.
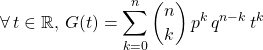
![]() .
.
Correction de l’exercice sur l’utilisation de la fonction génératrice
Question 1 :
Il est important de remarquer que si l’on tire ![]() au rang
au rang ![]() , tous les numéros tirés ensuite ne permettent pas d’obtenir un maximum.
, tous les numéros tirés ensuite ne permettent pas d’obtenir un maximum.
Les événements ![]() et
et ![]() forment un système complet d’événements de probabilité non nulle. Par la formule des probabilités totales,
forment un système complet d’événements de probabilité non nulle. Par la formule des probabilités totales,
![]()
![]()
![]()
![]() Si
Si ![]() , le dernier tirage donne un numéro strictement inférieur à
, le dernier tirage donne un numéro strictement inférieur à ![]() , réaliser en tout
, réaliser en tout ![]() maximums entre le temps 1 et le temps
maximums entre le temps 1 et le temps ![]() revient donc à
revient donc à
obtenir ![]() maximums en tirant les
maximums en tirant les ![]() premiers numéros (tous les numéros de 1 à
premiers numéros (tous les numéros de 1 à ![]() sauf le numéro qui sort au rang
sauf le numéro qui sort au rang ![]() ), donc
), donc
![]()
![]() Si
Si ![]() , le dernier tirage donne
, le dernier tirage donne ![]() donc un numéro strictement supérieur aux
donc un numéro strictement supérieur aux ![]() numéros déjà tirés tous entre 1 et
numéros déjà tirés tous entre 1 et ![]() .
.
Réaliser en tout ![]() maximums entre le temps 1 et le temps
maximums entre le temps 1 et le temps ![]() revient donc à obtenir
revient donc à obtenir ![]() maximums en tirant les
maximums en tirant les ![]() premiers numéros, donc
premiers numéros, donc
![]()
On a donc obtenu
![]()
![]()
Question 2 :
Vrai
En sommant pour ![]() les relations déduites de Q4,
les relations déduites de Q4,
![]()
![]()
on obtient 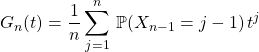
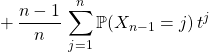
On pose ![]() dans la première somme et on utilise
dans la première somme et on utilise ![]()
pour obtenir
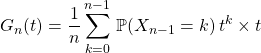
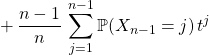
soit ![]()
soit ![]() .
.
Question 3 :
On note si ![]() ,
, 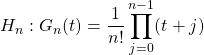 .
.
![]()
![]() , donc
, donc ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
Comme ![]()
alors 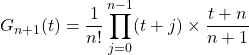
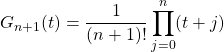 .
.
La propriété est vraie par récurrence sur ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Corrigé sur l’ajout d’une boule de couleur opposée en Maths Sup
Question 1 :
![]() si
si ![]() ou
ou ![]() car, entre deux tirages, le nombre de blanches est stable ou augmente d’une unité.
car, entre deux tirages, le nombre de blanches est stable ou augmente d’une unité.
Si ![]() est réalisé, on a
est réalisé, on a ![]() boules blanches et
boules blanches et ![]() noires,
noires,
![]()
![]()
et ![]()
![]() .
.
Question 2 :
La famille ![]() est un système complet d’événements.
est un système complet d’événements.
Par la formule des probabilités totales :
![]()
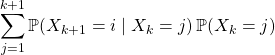
seuls les termes pour ![]() et
et ![]() sont à conserver
sont à conserver
si ![]() ,
,
![]()
![]()
![]()
Par la question 3,
![]()
![]()
![]()
![]()
Question 3 :
![]()
![]() .
.
La question précédente donne:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Correction sur le tirage de la première et la dernière en Maths Sup
Question 1 :
On traduit 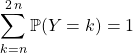 pour obtenir
pour obtenir 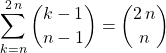
en posant ![]() ,
,
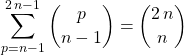
puis en remplaçant ![]() par
par ![]()
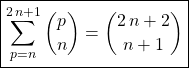 .
.
Question 2 :
avec ![]()
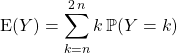
donc 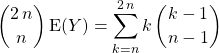
On utilise ![]()
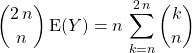
on peut donc utiliser la question précédente :
![]() (il manquait le terme pour
(il manquait le terme pour ![]() )
)
et par la formule du triangle de Pascal,
![]() .
.
Puis par quotient, ![]()
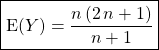 .
.
Question 3 :
![]()
![]() Par le théorème de transfert,
Par le théorème de transfert,
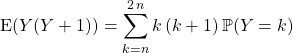
donc ![]()
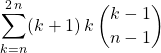
On utilise ![]()
![]()
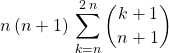
On pose ![]() ,
,
![]()
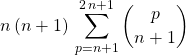
On peut donc utiliser la question 3 en remplaçant ![]() par
par ![]() et en remarquant qu’il manque les termes pour
et en remarquant qu’il manque les termes pour ![]() et
et ![]() :
:
![]()
![]()
Par le triangle de Pascal :
![]()
![]()
![]()
et avec le triangle de Pascal
![]() .
.
![]()
puis par quotient
![]()
![]()
![]()
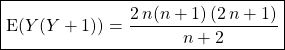 .
.
![]() Calcul de la variance.
Calcul de la variance.
![]()
![]()
![]()
![]()
![]()
![]()
après calculs : ![]() donc
donc
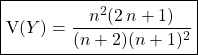 .
.
Correction de l’exercice sur la loi Hypergéométrique en Maths Sup
Si ![]() , on note
, on note ![]() la variable aléatoire égale à
la variable aléatoire égale à ![]() si l’on tire la boule blanche
si l’on tire la boule blanche ![]() et
et ![]() sinon.
sinon.
Pour réaliser ![]() , on prend la boule
, on prend la boule ![]() et on ajoute
et on ajoute ![]() boules choisies parmi les
boules choisies parmi les ![]() autres boules.
autres boules.
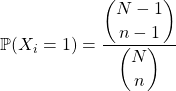
![]()
![]() .
.
Comme 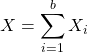 ,
, 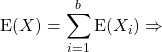
![]() .
.
Correction de l’éxercice sur le maximum et minimum de 2 tirages
Question 1 :
Vrai
On note ![]() .
.
![]() .
.
Si ![]() ,
,
![]()
![]()
![]()
Donc ![]() et
et ![]() suivent la même loi.
suivent la même loi.
Question 2 :
![]()
![]()
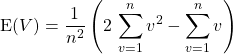
![]()
![]() .
.
![]()
![]()
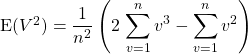
![]()
![]()
![]()
![]()
![]()
![]()
après factorisation et réduction au même dénominateur ,
![]()
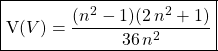 .
.
Correction de l’exercice sur deux variables de loi uniforme
Question 1 :
![]() On calcule
On calcule ![]() en utilisant le même type de raisonnement que dans la question précédente.
en utilisant le même type de raisonnement que dans la question précédente.
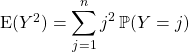
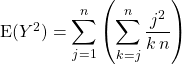
que l’on écrit sous la forme
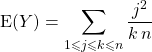
ce qui permet d’intervertir les signes ![]()
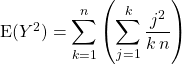
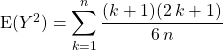
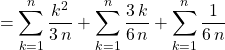
![]()
![]() .
.
![]() Variance
Variance
![]()
![]()
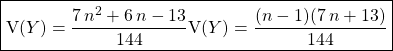 .
.
Question 2 :
Vrai
La variable ![]() est à valeurs dans
est à valeurs dans ![]() car
car ![]() , donc
, donc ![]() .
.
Puis ![]() et
et ![]()
D’autre part, ![]() prend la valeur
prend la valeur ![]() lorsque par exemple
lorsque par exemple ![]() et
et ![]() .
.
Donc ![]() .
.
Si ![]() ,
,
![]()
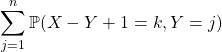
en utilisant le système complet d’événements ![]() ,
,
![]()
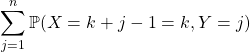
il ne faut garder que les indices ![]() vérifiant
vérifiant ![]() ssi
ssi ![]()
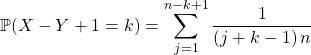
Puis en posant ![]() ,
,
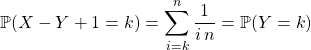
donc ![]() a même loi que
a même loi que ![]() .
.
Nos cours en ligne en maths pour les Maths Sup proposent également des exercices sur d’autres chapitres, par exemple :

