Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Fonctions usuelles en Maths Sup MPSI, PCSI, MP2I et PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Fonctions usuelles en Maths Sup
Plan :
1. Révision des fonctions exponentielle et logarithme.
2. Fonctions puissances
3. Fonctions ch, sh et th
4. Fonctions réciproques des fonctions circulaires
5. Utiliser les fonctions réciproques des fonctions circulaires
Retrouvez nos professeurs particuliers de maths sur notre plateforme pour vous aider à consolider vos notions en prépa scientifique.
1. Révision des fonctions exponentielle et logarithme
1.1. Bijections réciproques en Maths Sup
![]()
![]()
sont des bijections réciproques l’une de l’autre :
![]() ssi
ssi ![]()
1.2. Propriétés des dérivées
![]() La fonction
La fonction ![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
![]() La fonction
La fonction ![]() est dérivable sur
est dérivable sur ![]() de fonction dérivée :
de fonction dérivée : ![]() .
.
![]() ⚠️ Si
⚠️ Si ![]() est une fonction dérivable sur
est une fonction dérivable sur ![]() et ne s’annulant pas, la dérivée de
et ne s’annulant pas, la dérivée de ![]() est
est ![]() .
.
![]() La fonction
La fonction ![]() est dérivable sur
est dérivable sur ![]() de fonction dérivée
de fonction dérivée ![]() .
.
![]()
![]() est la seule fonction vérifiant les conditions
est la seule fonction vérifiant les conditions
![]() et
et ![]()
![]()
![]() vérifie
vérifie ![]() ssi
ssi ![]() .
.
![]() Si
Si ![]() est une fonction dérivable sur
est une fonction dérivable sur ![]() la fonction dérivée de
la fonction dérivée de ![]() est
est ![]() .
.
1.3. Propriétés algébriques des fonctions usuelles en Maths Sup
![]() Pour la fonction
Pour la fonction ![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() .
.
![]() Pour la fonction
Pour la fonction ![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() .
.
1.4. Les limites et inégalités classiques des fonctions usuelles en Maths Sup
![]() Pour la fonction
Pour la fonction ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Le graphe de ![]() est situé sous la tangente en
est situé sous la tangente en ![]()
Démonstration des deux derniers résultats : ![]() Soit
Soit ![]() ,
, ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
Donc
![]()
![]() On étudie
On étudie ![]() .
.
![]() ,
,
![]() est décroissante sur
est décroissante sur ![]() et croissante sur
et croissante sur ![]() et admet un minimum en
et admet un minimum en ![]() .
.
![]() Pour la fonction exponentielle.
Pour la fonction exponentielle.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Le graphe de ![]() est situé au-dessus la tangente en
est situé au-dessus la tangente en ![]()
Démonstration des deux derniers résultats : ![]() Soit
Soit ![]() ,
, ![]() ,
, ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
Donc ![]() .
.
![]() On étudie
On étudie ![]() .
.
![]() ,
, ![]() est décroissante sur
est décroissante sur ![]() et croissante sur
et croissante sur ![]() et admet un minimum en
et admet un minimum en ![]() .
.
Il suffit d’utiliser ![]() pour obtenir :
pour obtenir : ![]() si
si ![]() .
.
Une limite classique
![]() .
.
Correction : ![]() Le résultat est évident si
Le résultat est évident si ![]() .
.
![]() On suppose dans la suite que
On suppose dans la suite que ![]() .
.
On note ![]() .
.
Comme ![]() il existe un entier
il existe un entier ![]() tel que si
tel que si ![]() ,
, ![]() , on peut alors calculer
, on peut alors calculer ![]() :
:
![]() .
.
![]()
![]() donne :
donne :
![]()
![]()
Par continuité de la fonction exponen- tielle, ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
2. Fonction puissance des fonctions usuelles
2.1. Définition de puissance de fonctions usuelles en Maths Sup
Rappel
![]() Si
Si ![]() est définie et dérivable sur
est définie et dérivable sur ![]() .
.
![]() Si
Si ![]() est définie et dérivable sur
est définie et dérivable sur ![]() .
.
Définition de la fonction puissance.
On généralise cette définition en posant
![]() si
si ![]() et
et ![]() ,
, ![]() .
.
2.2. Propriétés algébriques de puissance de fonctions usuelles en Maths Sup
![]()
![]() si
si ![]() , cette définition coïncide avec
, cette définition coïncide avec ![]() lorsque
lorsque ![]() .
.
![]() si
si ![]() , cette définition coïncide avec
, cette définition coïncide avec ![]() lorsque
lorsque ![]() .
.
![]() si
si ![]() avec
avec ![]() ,
, ![]() ,
, ![]() lorsque
lorsque ![]() .
.
![]() si
si ![]() et
et ![]()
![]()
![]()
![]()
![]() si
si ![]() et
et ![]() ,
,
![]()
![]() si
si ![]() et
et ![]()
![]() .
.
2.3. Propriétés en analyse de puissance de fonctions usuelles en Maths Sup
Soit ![]() et
et ![]()
![]() Etude lorsque
Etude lorsque ![]() .
.
![]()
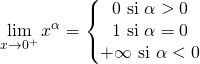
![]()
![]() est prolongeable par continuité en
est prolongeable par continuité en ![]() par
par ![]() si
si ![]() ,
, ![]() si
si ![]() .
.
![]() Dérivée
Dérivée
![]() Si
Si ![]() .
.
![]()
![]() est strictement croissante si
est strictement croissante si ![]() et strictement décroissante si
et strictement décroissante si ![]() .
.
![]() Si
Si ![]() , le graphe de
, le graphe de ![]() admet une demi-tangente horizontale en
admet une demi-tangente horizontale en ![]() si
si ![]() , verticale si
, verticale si ![]() .
.
![]() Limite en
Limite en ![]() .
.
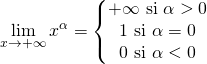
2.4. Croissance comparée en Maths Sup
![]() Pour tout
Pour tout ![]() .
.
![]() Pour tout
Pour tout ![]() ,
,
![]() et
et ![]()
![]() Pour tout
Pour tout ![]() et
et ![]() ,
,
![]()
![]() .
.
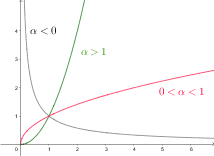
2.5. Une limite classique de fonctions usuelles en Maths Sup
Si ![]()
Donc
3. Fonctions hyperboliques en Maths Sup
3.1. Définition et propriétés algébriques de fonctions hyperboliques
![]() On définit pour tout réel
On définit pour tout réel ![]() ,
,
![]()
![]() .
.
![]() Conséquences : pour tout réel
Conséquences : pour tout réel ![]() ,
,
![]()
![]()
![]() .
.
3.2. Étude de fonctions hyperboliques en Maths Sup
![]() ch et sh sont respectivement paire et impaire, dérivables avec
ch et sh sont respectivement paire et impaire, dérivables avec ![]() et
et ![]()
ch et sh sont strictement croissantes sur ![]() .
.
Elles admettent ![]() pour limite en
pour limite en ![]() .
.
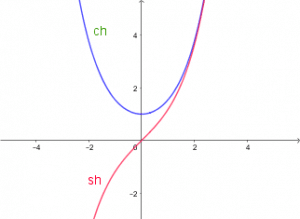
3.3. Fonction tangente hyperbolique en Maths Sup
On définit pour ![]() ,
, ![]()
On peut écrire ![]()
![]()
![]()
![]() est continue, impaire strictement croissante sur
est continue, impaire strictement croissante sur ![]() et admet
et admet ![]() (resp.
(resp.![]() ) pour limite en
) pour limite en ![]() (resp
(resp ![]() .)
.)
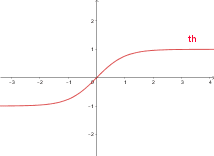
3.4. Des limites classiques de fonctions hyperboliques
![]()
![]()
![]()
![]()
(par utilisation du taux d’accroisse- ment en 0).
3.5. Résultats en exercices des fonctions hyperboliques
Résultat 1
![]() Si
Si ![]() et
et ![]() ,
, ![]()
![]() Si
Si ![]() ,
, ![]() .
.
Démonstration : ![]() Si
Si ![]() et
et ![]() ,
,
![]() donne
donne
![]()
puis comme ![]() si
si ![]() ,
, ![]()
![]() Si
Si ![]() ,
,
![]() donne
donne
![]()
puis comme ![]() ,
, ![]()
Résultat 2
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() et
et ![]() définit une bijection de
définit une bijection de ![]() sur lui-même.
sur lui-même.
Expression de sa fonction réciproque et dérivabilité.
Correction : ![]() Existence de la réciproque de la fonction ch.
Existence de la réciproque de la fonction ch.
![]()
![]() est continue et strictement croissante sur
est continue et strictement croissante sur ![]() et vérifie
et vérifie ![]() , donc
, donc
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
![]() Expression de la réciproque.
Expression de la réciproque.
![]() Première méthode.
Première méthode.
Soit si ![]() ,
, ![]() avec
avec ![]() .
.
On a vu que ![]() .
.
On termine avec ![]()
donc ![]() .
.
![]() Deuxième méthode (plus compliquée)
Deuxième méthode (plus compliquée)
Si ![]() , on résout l’équation
, on résout l’équation ![]() avec
avec ![]() .
.
On obtient l’équation
![]()
![]()
L’équation ![]() admet deux solutions :
admet deux solutions :
![]() et
et ![]() de somme égale à
de somme égale à ![]() et de produit égal à 1, donc toutes deux positives si
et de produit égal à 1, donc toutes deux positives si ![]() et vérifiant donc
et vérifiant donc ![]() , ce qui donne
, ce qui donne ![]() , soit
, soit ![]() .
.
La fonction réciproque de ![]() est la bijection de
est la bijection de ![]() sur
sur ![]() définie par
définie par ![]() .
.
Elle est notée ![]() .
.
![]() Dérivée
Dérivée
![]() La fonction
La fonction ![]() étant dérivable de dérivée non nulle sur
étant dérivable de dérivée non nulle sur ![]() ,
, ![]() est dérivable sur
est dérivable sur ![]() et
et
![]()
en notant ![]() soit
soit ![]() , on a vu que
, on a vu que
![]()
donc ![]() .
.
Résultat 3
![]() définit une bijection de
définit une bijection de ![]() sur lui-même.
sur lui-même.
Expression de sa fonction réciproque et dérivabilité.
Démonstration : ![]() Existence de la réciproque de la fonction sh.
Existence de la réciproque de la fonction sh.
![]() est continue et strictement croissan- te sur
est continue et strictement croissan- te sur ![]() et vérifie
et vérifie ![]() et
et ![]() ,
,
donc ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
![]() Calcul de la réciproque
Calcul de la réciproque
![]() Première méthode (plus simple).
Première méthode (plus simple).
On a vu que si ![]() ,
, ![]()
On termine avec ![]()
donc ![]() .
.
![]() Deuxième méthode (plus lourde)
Deuxième méthode (plus lourde)
Si ![]() , on résout l’équation
, on résout l’équation ![]() .
.
On obtient l’équation
![]()
![]()
L’équation ![]() admet deux solutions
admet deux solutions
![]() et
et ![]()
![]() , soit
, soit ![]() .
.
La fonction réciproque de ![]() est la bijection de
est la bijection de ![]() sur
sur ![]() définie par
définie par ![]() .
.
Elle est notée ![]()
![]() Dérivée
Dérivée
La fonction ![]() étant dérivable de dérivée non nulle sur
étant dérivable de dérivée non nulle sur ![]() ,
, ![]() est dérivable sur
est dérivable sur ![]() et
et
![]()
en notant ![]() soit
soit ![]() , on a vu que
, on a vu que
![]()
donc ![]() .
.
Résultat 4
Montrer que la fonction th admet une fonction réciproque, la déterminer et calculer sa dérivée.
Démonstration : ![]() Existence
Existence
![]() est continue, strictement croissante sur
est continue, strictement croissante sur ![]() et admet
et admet ![]() (resp.
(resp. ![]() ) pour limite en
) pour limite en ![]() (resp
(resp ![]() .)
.)
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
![]() Calcul
Calcul
On résout ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]() .
.
La fonction réciproque de la fonction ![]() notée
notée ![]() est définie sur
est définie sur ![]() par
par ![]() .
.
![]() Dérivée
Dérivée
Sa dérivée est ![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
4. Fonctions réciproques des fonctions circulaires en Maths Sup
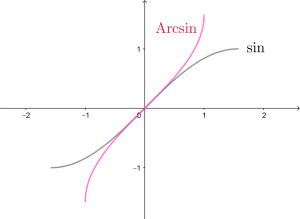
4.1. Fonction Arcsinus en Maths Sup
![]() La fonction
La fonction ![]() définit une bijection strictement croissante de
définit une bijection strictement croissante de ![]() sur
sur ![]() .
.
Sa fonction réciproque ![]() est une bijection strictement croissante de
est une bijection strictement croissante de ![]() à valeurs dans
à valeurs dans ![]() , dérivable sur
, dérivable sur ![]() .
.
![]()
La fonction Arcsinus est impaire.
![]()
![]()
⚠️![]()
alors qu’il faudra faire attention
![]()
![]()
👍 le « A » situé en début d’expression dans ![]() doit vous mener à faire Attention alors qu’il n’est pas nécessaire de faire attention lorsqu’il est « caché » dans
doit vous mener à faire Attention alors qu’il n’est pas nécessaire de faire attention lorsqu’il est « caché » dans ![]() .
.
👍 On peut retenir : Arcsin![]() est l’arc de
est l’arc de ![]() dont le sinus est égal à
dont le sinus est égal à ![]() .
.
![]() Si
Si ![]() ,
, ![]()
car ![]() et
et ![]() lorsque
lorsque ![]() .
.
![]()
![]() .
.
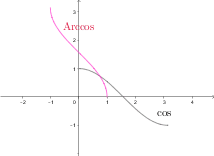
4.2. Arccosinus en Maths Sup
![]() La fonction
La fonction ![]() définit une bijection strictement décroissante de
définit une bijection strictement décroissante de ![]() sur
sur ![]() .
.
Sa fonction réciproque ![]() est une bijection strictement décroissante de
est une bijection strictement décroissante de ![]() à valeurs dans
à valeurs dans ![]() , dérivable sur
, dérivable sur ![]() et
et
![]()
![]()
![]() .
.
⚠️ ![]()
alors qu’il faudra faire attention
![]()
![]() .
.
👍 le « A » situé en début d’expression dans ![]() doit vous mener à faire Attention alors qu’il n’est pas nécessaire de faire attention lorsqu’il est « caché » dans
doit vous mener à faire Attention alors qu’il n’est pas nécessaire de faire attention lorsqu’il est « caché » dans ![]() .
.
![]()
![]()
![]() .
.
👍On peut retenir : Arccos![]() est l’arc de
est l’arc de ![]() dont le cosinus est égal à
dont le cosinus est égal à ![]() .
.
![]() Si
Si ![]() ,
, ![]()
car ![]() et
et ![]() lorsque
lorsque ![]() .
.
![]()
![]()
![]() .
.
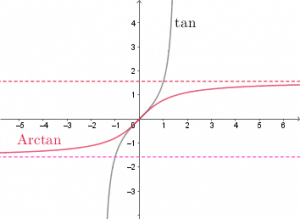
4.3. Arctangente en Maths Sup
![]() La fonction
La fonction ![]() définit une bijection strictement croissante de
définit une bijection strictement croissante de ![]() sur
sur ![]() .
.
Sa fonction réciproque ![]() est une bijection strictement croissante de
est une bijection strictement croissante de ![]() à valeurs dans
à valeurs dans ![]() , dérivable sur
, dérivable sur ![]() et
et
![]()
![]()
![]()
⚠️ ![]()
alors qu’il faudra faire attention
![]()
![]()
👍 le « A » situé en début d’expression dans ![]() doit vous mener à faire Attention alors qu’il n’est pas nécessaire de faire attention lorsqu’il est « caché » dans
doit vous mener à faire Attention alors qu’il n’est pas nécessaire de faire attention lorsqu’il est « caché » dans ![]() .
.
![]() La fonction Arctangente est impaire.
La fonction Arctangente est impaire.
👍 On peut retenir : Arctan![]() est l’arc de
est l’arc de ![]() dont la tangente est égale à
dont la tangente est égale à ![]() .
.
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]() .
.
Démonstration des 2 derniers résultats : ![]() Soit
Soit ![]() ,
, ![]() ,
, ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
Donc ![]()
![]() On note
On note ![]() .
.
![]() et
et ![]() lorsque
lorsque ![]() .
.
Puis ![]() .
.
![]()
et ![]() .
.
![]()
![]()
![]()
(démonstration dans le § suivant)
5. Utiliser les fonctions réciproques des fonctions circulaires
5.1. Résoudre une équation avec des fonctions circulaires en Maths Sup
Soit à résoudre une équation du type ![]() où
où ![]() contient des fonctions circulaires réciproques.
contient des fonctions circulaires réciproques.
![]() Vérifier que l’équation admet au moins une solution (en général en étudiant les variations de
Vérifier que l’équation admet au moins une solution (en général en étudiant les variations de ![]() et en utilisant le théorème des valeurs intermédiaires ou le théorème de la bijection). En déterminer le nombre et éventuellement les encadrer.
et en utilisant le théorème des valeurs intermédiaires ou le théorème de la bijection). En déterminer le nombre et éventuellement les encadrer.
![]() Commencer par un raisonnement par analyse, calculer le sinus, le cosinus ou la tangente de l’équation écrite sous une forme éventuellement transformée pour que les calculs soient simples.
Commencer par un raisonnement par analyse, calculer le sinus, le cosinus ou la tangente de l’équation écrite sous une forme éventuellement transformée pour que les calculs soient simples.
On obtient des conditions nécessaires sur les valeurs des solutions.
![]() Si le nombre de solutions obtenues dans la partie analyse est égal au nombre de solutions attendues, on a obtenu les solutions et le problème est résolu.
Si le nombre de solutions obtenues dans la partie analyse est égal au nombre de solutions attendues, on a obtenu les solutions et le problème est résolu.
Si l’on obtient plus de valeurs que de solutions attendues, il faut « faire le tri » et ne retenir en synthèse que les solutions convenables. En général on peut conclure par des arguments d’encadrement.
Exemple
Résoudre ![]() .
.
Correction : ![]() Existence d’une solution
Existence d’une solution
La fonction ![]() est continue sur
est continue sur ![]() et strictement croissante comme somme de deux fonctions strictement croissantes. Elle admet
et strictement croissante comme somme de deux fonctions strictement croissantes. Elle admet ![]() (resp.
(resp. ![]() ) pour limite en
) pour limite en ![]() (resp. en
(resp. en ![]() ).
).
Elle définit une bijection de ![]() sur
sur ![]() .
.
Comme ![]() , il existe un unique
, il existe un unique ![]() tel que
tel que ![]() .
.
![]() Recherche de valeurs nécessaires.
Recherche de valeurs nécessaires.
![]() donne
donne
![]()
en utilisant ![]() ,
,
on obtient :
![]()
![]()
![]()
Cette équation admet deux solutions ![]() et
et ![]()
![]() Fin du raisonnement
Fin du raisonnement
On avait prouvé l’existence et l’unicité de la solution de l’équation et prouvé que ![]() .
.
On a trouvé deux valeurs nécessaires ![]() et
et ![]() .
.
La solution de l’équation est donc ![]() soit
soit ![]() .
.
5.2. Transformer une expression avec des fonctions circulaires en Maths Sup
Soit ![]() l’expression à transformer.
l’expression à transformer.
![]() Commencer par chercher le domaine de définition de la fonction
Commencer par chercher le domaine de définition de la fonction ![]() , éventuellement restreindre le domaine d’étude en faisant appel à des considérations de parité.
, éventuellement restreindre le domaine d’étude en faisant appel à des considérations de parité.
Dans la suite, on note ![]() l’ensemble sur lequel on veut simplifier
l’ensemble sur lequel on veut simplifier ![]() .
.
![]() M1. Si
M1. Si ![]() , à vous de choisir entre les changements de variables
, à vous de choisir entre les changements de variables ![]() ou
ou ![]() ,
,
Sinon, poser ![]() .
.
Dans les deux cas, préciser l’ensemble de définition ![]() de
de ![]() et
et ![]() de
de ![]() .
.
Utiliser vos formules de trigonométries préférées pour simplifier l’équation et terminer en donnant les résultats en fonction de ![]() .
.
⚠️ ![]() n’est qu’une variable auxiliaire qui doit disparaître dans les résultats à la fin.
n’est qu’une variable auxiliaire qui doit disparaître dans les résultats à la fin.
![]() M2. Il est possible aussi de chercher à dériver (en précisant bien le domaine
M2. Il est possible aussi de chercher à dériver (en précisant bien le domaine ![]() où l’on dérive), simplifier l’expres- sion de
où l’on dérive), simplifier l’expres- sion de ![]() et en reconnaissant la dérivée d’une fonction
et en reconnaissant la dérivée d’une fonction ![]() simple, on peut utiliser le résultat suivant :
simple, on peut utiliser le résultat suivant :
Soient ![]() un intervalle et
un intervalle et ![]() l’intervalle
l’intervalle ![]() privé de ses bornes.
privé de ses bornes.
Si les fonctions ![]() et
et ![]() sont continues sur
sont continues sur ![]() et dérivables sur
et dérivables sur ![]() et si
et si ![]() ,
,
alors ![]() est constante sur
est constante sur ![]() .
.
On détermine cette constante, en calculant ![]() où
où ![]() ou en cherchant la limité de
ou en cherchant la limité de ![]() en l’une des bornes de
en l’une des bornes de ![]() .
.
Exemple
En utilisant la première méthode, calculer ![]() .
.
Correction : ![]() est défini ssi
est défini ssi ![]()
![]() .
.
On simplifie ![]() pour
pour ![]() .
.
![]()
![]()
![]()
![]()
![]()
Puis comme ![]() ,
,
![]()
donc ![]() .
.
On en déduit puisque ![]() est impaire :
est impaire :
![]() .
.
Exemple
En utilisant une dérivée, calculer ![]() .
.
Correction : On note si ![]() ,
, ![]() .
.
![]() est impaire et dérivable sur
est impaire et dérivable sur ![]() .
.
Si ![]()
![]() .
.
![]() est donc constante sur
est donc constante sur ![]() .
.
Pour déterminer cette constante,
![]() on peut utiliser
on peut utiliser ![]()
![]() ou utiliser la limite de
ou utiliser la limite de ![]() en
en ![]() : cette limite est égale à
: cette limite est égale à ![]() .
.
Les deux calculs donnent
![]() .
.
Puis comme ![]() ,
,
si ![]() .
.
On a donc redémontré que
![]()
![]() .
.
D’autres cours de Maths au programme de Maths Sup pour les filières PTSI, PCSI et MPSI sont également accessibles gratuitement :

