Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés de Fonctions usuelles en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Fonction Hyperbolique et suite de Fibonacci
1. Fonctions hyperboliques et puissances
2. Résolutions d’équations avec des fonctions circulaires réciproques
3. Transformation d’expressions de fonctions circulaires réciproques
4. Un mélange
5. Suite de Fibonacci et Arctangente
6. Fonction réciproque
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Fonctions hyperboliques et puissances
Exercice 1
Résoudre l’équation ![]()
Correction : On cherche des solutions ![]() .
.
L’équation est équivalente à
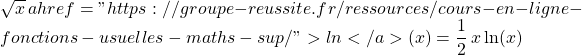
ssi ![]()
ssi ![]() ou
ou ![]()
ssi ![]() ou
ou ![]() .
.
L’équation admet deux solutions : ![]() et
et ![]() .
.
Exercice 2
Résoudre ![]()
Correction : On suppose ![]() .
.
L’équation est équivalente à
![]()
ssi ![]() .
.
On note ![]()
![]()
![]() .
.
![]() s’annule en
s’annule en ![]() et
et ![]() admet un minimum en ce point car
admet un minimum en ce point car ![]() est décroissante sur
est décroissante sur ![]() et croissante sur
et croissante sur ![]() .
.
![]() (on rappelle que
(on rappelle que ![]() et
et ![]() )
)
alors ![]() s’annule sur
s’annule sur ![]() et sur
et sur![]() .
.
Je vous conseille de faire le tableau de variations !
On cherche une solution de la forme ![]() .
.
![]()
ssi ![]() .
.
Il y a deux solutions évidentes : ![]() et
et ![]() .
.
On a donc obtenu
![]() et
et ![]() .
.
Comme on sait qu’il n’y a que deux solutions, ce sont ![]() .
.
Exercice 3
Résoudre ![]()
Correction : On utilise ![]()
![]()
![]()
donc ![]() .
.
Donc en posant ![]() ,
, ![]() donne
donne ![]() soit
soit ![]() .
.
Cette équation admet deux racines dont une seule est positive :
on en déduit que ![]() .
.
Exercice 4
Calculer ![]() puis
puis ![]() .
.
il y a deux solutions opposées : On note ![]() et
et ![]() .
.
On commence par résoudre
![]()
ssi ![]()
ssi ![]() .
.
Soit l’équation ![]() .
.
![]()
![]()
L’équation a pour racines :
![]() et
et ![]() .
.
On obtient donc
![]() ou
ou ![]()
ssi ![]() ou
ou ![]()
ssi ![]() ou
ou ![]()
ssi ![]()
ou ![]()
ssi ![]() .
.
L’équation admet deux solutions ![]() et
et ![]() .
.
Exercice 5
Si ![]() , simplifier
, simplifier ![]() .
.
Correction : On utilise ![]()
![]()
Avec ![]()
![]()
en multipliant par la quantité conjuguée,
![]()
![]()
puis ![]()
![]() .
.
Exercice 6
Pour tout ![]() ,
, ![]() .
.
Correction : Soit ![]() .
.
![]() est dérivable sur
est dérivable sur ![]()
et ![]()
![]()
On note ![]() et
et ![]() .
.
Il est évident que ![]() ce qui permet une factorisation de la forme
ce qui permet une factorisation de la forme
![]()
(on a trouvé le coefficient de ![]() par identification des termes en
par identification des termes en ![]() et du terme constant en identifiant les coefficients constants, on obtient par calcul simple
et du terme constant en identifiant les coefficients constants, on obtient par calcul simple ![]() ).
).
![]()
sachant que si ![]() , donc
, donc ![]() et alors
et alors ![]() si
si ![]() .
.
On en déduit que si ![]() ,
, ![]() .
.
![]() est croissante sur
est croissante sur ![]() et
et ![]() , donc si
, donc si ![]() .
.
2. Résolutions d’équations avec des fonctions circulaires réciproques
Exercice 1
Résoudre ![]() .
.
Correction : ![]() Existence d’une solution
Existence d’une solution
![]() est une fonction continue et strictement croissante sur
est une fonction continue et strictement croissante sur ![]()
![]() .
.
Comme ![]() est impaire,
est impaire, ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
Il existe un unique ![]() tel que
tel que ![]() .
.
Comme de plus ![]() , on en déduit que
, on en déduit que ![]() .
.
![]() Résolution par condition nécessaire
Résolution par condition nécessaire
On rappelle que ![]() Les calculs sont plus simples en calculant
Les calculs sont plus simples en calculant ![]() .
.
Sachant que ![]()
![]()
ssi ![]()
soit ![]()
puis en élevant au carré, on obtient la condition nécessaire :
![]()
![]() .
.
L’équation ![]() admet une seule racine positive :
admet une seule racine positive :
![]() .
.
![]() Conclusion: Il reste donc à résoudre
Conclusion: Il reste donc à résoudre ![]() sachant que
sachant que ![]() ,
, 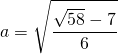
On a prouvé qu’il y avait au plus une solution positive et on sait que l’équation admet une et une seule solution.
C’est donc le réel 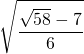 .
.
Exercice 2
Résoudre
![]()
![]()
Correction : ![]() Existence de solutions
Existence de solutions
On note si ![]()
![]()
![]() est décroissante et
est décroissante et ![]() est croissante, donc
est croissante, donc ![]() est décroissante et
est décroissante et ![]() est croissante sur
est croissante sur ![]() et sur
et sur ![]() .
.
![]() et
et ![]()
![]()
![]()
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() et une bijection de
et une bijection de ![]() sur
sur ![]() .
.
Comme ![]() , l’équation admet une unique solution strictement positive.
, l’équation admet une unique solution strictement positive.
On peut préciser que cette solution est supérieure à 1 car ![]()
![]() Résolution par condition nécessaire
Résolution par condition nécessaire
On cherche donc ![]() tel que
tel que ![]()
![]()
et en utilisant ![]() ,
,
![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]() .
.
Cette équation admet deux solutions ![]() et
et ![]() .
.
On a vu que l’équation n’admet qu’une seule solution qui est supérieure à 1, donc il s’agit de ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Transformation d’expressions de fonctions circulaires réciproques
Exercice 1
Calculer ![]()
Correction : ![]() En utilisant la stricte croissance de la fonction Arctan et
En utilisant la stricte croissance de la fonction Arctan et ![]() ,
,
![]()
et ![]() .
.
Si ![]() ,
, ![]() , ce qui permet de calculer
, ce qui permet de calculer ![]() .
.
![]() On utilise
On utilise ![]()
On calcule d’abord ![]()
puis ![]() donc
donc ![]() tel que
tel que ![]() .
.
Sachant que ![]() , on a prouvé que
, on a prouvé que ![]() .
.
soit ![]() .
.
Exercice 2
Calculer ![]()
Correction : Soit ![]() ,
, ![]()
![]()
![]()
or ![]() et
et ![]()
Donc ![]() .
.
puis ![]()
soit ![]() ,
,
![]() car
car ![]() .
.
Exercice 3
Simplifier ![]()
Correction : ![]() Définition de
Définition de ![]()
![]() est défini
est défini
ssi ![]() et
et ![]()
ssi ![]() et
et ![]()
ssi ![]() et
et ![]()
ssi ![]() et
et ![]()
On en déduit que ![]() est définie sur
est définie sur ![]() .
.
De plus ![]() car
car ![]() .
.
![]() On simplifie d’abord
On simplifie d’abord ![]() si
si ![]() .
.
On pose ![]()
![]()
![]()
![]()
![]() car
car ![]() .
.
![]()
![]()
![]() et
et ![]() .
.
On doit donc distinguer deux cas :
![]()
![]()
ssi ![]() ssi
ssi ![]()
ssi ![]() ,
,
![]() .
.
![]()
![]()
ssi ![]()
ssi ![]() ,
,
![]()
donc ![]() .
.
De plus ![]() , donc
, donc
![]() .
.
![]() Lorsque
Lorsque ![]() avec
avec ![]() .
.
On distingue donc deux cas :
![]() si
si ![]() ,
,
![]()
![]()
![]() si
si ![]() ,
,
![]()
![]() .
.
En résumé
![]() si
si ![]() ,
,
![]()
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() ,
, ![]()
Vous trouverez une autre démonstration dans le chapitre dérivées en Maths Sup et la tâche méthodes.
4. Un mélange
Exercice 1
Simplifier si ![]() est réel
est réel ![]() .
.
Correction : On note ![]() .
.
![]() est définie et dérivable sur
est définie et dérivable sur ![]() car th est à valeurs dans
car th est à valeurs dans ![]() .
.
Si ![]() est réel,
est réel,
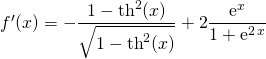
![]()
En utilisant ![]() et
et ![]() ,
,
![]()
![]()
![]() .
.
La fonction ![]() est constante sur
est constante sur ![]() et
et ![]()
![]() .
.
Pour tout réel ![]() ,
, ![]() .
.
Exercice 2
Question 1
Pour tout ![]() , il existe un unique
, il existe un unique ![]() tel que
tel que ![]()
Correction : Si ![]() ,
, ![]() donc
donc ![]() , donc il existe un unique
, donc il existe un unique ![]() tel que
tel que ![]() et plus précisément
et plus précisément ![]() .
.
Exercice 2 (fin)
Question 2
![]() et
et ![]()
Correction : ![]() avec
avec ![]() .
.
![]()
![]() donc
donc
![]()
![]() .
.
Puis comme ![]() et
et ![]() par les hypothèses sur
par les hypothèses sur ![]() et
et ![]() , on a prouvé que
, on a prouvé que ![]() .
.
![]() On rappelle que
On rappelle que ![]()
![]()
![]()
![]()
![]()
![]()
![]()
puis ![]()
![]()
et ![]()
![]()
![]()
![]()
![]()
donc ![]() .
.
5. Suite de Fibonacci et 
On définit la suite de Fibonacci ![]() par
par
![]() ,
,
![]() et
et ![]() .
.
Question 1
Compléter l’identité de Cassini :
![]()
Correction : Si ![]() , on note
, on note ![]()
![]() Pour
Pour ![]() ,
,
![]() .
.
La propriété est vraie.
![]() On suppose que
On suppose que ![]() est vraie, on note
est vraie, on note ![]()
![]()
![]()
![]()
![]()
![]()
ce qui donne la relation au rang ![]() .
.
La propriété est démontrée par récurrence.
En déduire que, pour tout
Correction : ![]() La suite
La suite ![]() est une suite strictement croissante d’entiers, et
est une suite strictement croissante d’entiers, et ![]() , donc si
, donc si ![]() .
.
Si ![]() donc
donc ![]() vérifie
vérifie ![]() .
.
![]() On peut calculer
On peut calculer ![]() .
.
En utilisant ![]() ,
,
on obtient ![]()
![]()
![]() Transformation de cette relation
Transformation de cette relation
Puis on utilise ![]()
![]()
et ![]()
soit ![]() .
.
On obtient alors :
![]()
![]()
et ![]()
![]() .
.
Sachant que ![]() ,
,
![]() .
.
Donc ![]()
ce qui donne pour tout ![]() ,
,
![]()
![]()
Question 3
Si ![]() , simplifier
, simplifier 
Quelles identités particulières obtient- on pour ![]() ?
?
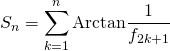
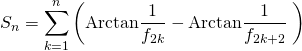
par télescopage
avec ![]() :
:
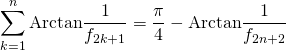
soit
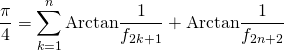
![]() On utilise ensuite
On utilise ensuite ![]()
![]() .
.
La relation précédente donne
![]() pour
pour ![]()
![]()
![]() pour
pour ![]()
![]()
![]() pour
pour ![]()
![]()
![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
6.Fonction réciproque
Montrer que la fonction ![]()
admet une fonction réciproque et la déterminer.
Correction : ![]()
![]() est continue et strictement croissante sur
est continue et strictement croissante sur ![]() admet
admet ![]() (resp.
(resp. ![]() ) pour limite en
) pour limite en ![]() (resp. en
(resp. en ![]() ).
).
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
Comme ![]() est impaire, la fonction réciproque
est impaire, la fonction réciproque ![]() est impaire (car si
est impaire (car si ![]() alors
alors ![]() donc
donc ![]() ).
).
![]() , donc
, donc ![]() prend la valeur
prend la valeur ![]() sur
sur ![]() .
.
![]() Résolution de
Résolution de ![]() (avec
(avec ![]() ).
).
![]()
ssi ![]()
ssi ![]() ssi
ssi ![]() ssi
ssi ![]() car
car ![]() .
.
On en déduit que ![]()
et ![]()
![]() donc
donc ![]()
![]() On calcule si
On calcule si ![]() et
et ![]() ,
,
![]()
ssi ![]() .
.
Comme ![]() , cette équation admet deux racines
, cette équation admet deux racines
![]()
![]() et
et ![]() .
.
On sait que ![]() , les deux racines sont de signe contraire.
, les deux racines sont de signe contraire.
![]() Si
Si ![]()
![]() .
.
Lorsque ![]() et on doit retenir la racine positive, on en déduit que
et on doit retenir la racine positive, on en déduit que ![]() .
.
![]() Si
Si ![]() .
.
Lorsque ![]() et on doit retenir la racine positive, on en déduit que
et on doit retenir la racine positive, on en déduit que ![]() .
.
![]() Conclusion
Conclusion
On a prouvé que si ![]()
![]()
![]() ,
, ![]()
et en utilisant ![]() impaire,
impaire,
si ![]() ,
, ![]()
![]() .
.
Plus de chapitres et de cours en maths grâce à nos cours en ligne de Maths pour les étudiants de prépa en Maths Sup :

