Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Fractions rationnelles en Maths Sup MPSI, MP2I, PCSI, PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Fractions rationnelles en Maths Sup
Plan :
1. Utiliser les propriétés et définitions
2. Décomposition en éléments simples dans ![]()
3. Décomposition en éléments simples dans ![]()
4. Méthodes de calcul.
1. Utiliser les propriétés et définitions
1.1. Propriétés de ![]()
![]() désigne un corps commutatif (
désigne un corps commutatif (![]() .
.
![]() est l’ensemble des fractions rationnelles, soit l’ensemble des quotients
est l’ensemble des fractions rationnelles, soit l’ensemble des quotients ![]() où
où ![]()
![]()
![]() .
.
On dit alors que ![]() et
et ![]() sont deux représentants de la fraction rationnelle.
sont deux représentants de la fraction rationnelle.
![]()
![]()
![]()
![]() est un corps commutatif, l’addition et la multiplication étant définies :
est un corps commutatif, l’addition et la multiplication étant définies :
Si ![]() et
et ![]() sont éléments de
sont éléments de ![]()
![]()
![]() .
.
![]()
![]()
![]() Si
Si ![]() et
et ![]() , il existe un unique couple
, il existe un unique couple ![]() tel que
tel que
![]()
![]() ,
,
![]()
![]() et
et ![]() n’ont pas de racine commu- ne dans
n’ont pas de racine commu- ne dans ![]()
![]()
![]() est unitaire.
est unitaire.
On dit que ![]() est la forme irréductible de
est la forme irréductible de ![]() .
.
Au second semestre, on dira que ![]() et
et ![]() sont premiers entre eux dans
sont premiers entre eux dans ![]() .
.
Toute autre représentation de ![]() est de la forme
est de la forme ![]() où
où ![]() ,
, ![]() .
.
1.2. Pôles
![]() Soit
Soit ![]() écrite sous forme irréductible.
écrite sous forme irréductible.
![]() Le nombre de racines dans
Le nombre de racines dans ![]() de
de ![]() est un ensemble fini
est un ensemble fini ![]() fini.
fini.
On définit la fonction rationnelle associée à ![]() par
par ![]() .
.
![]() Si
Si ![]() et si
et si ![]() ,
, ![]() .
.
![]() Soit
Soit ![]() écrite sous forme irréductible.
écrite sous forme irréductible.
Les pôles de ![]() sont les racines dans de
sont les racines dans de ![]() .
.
Si ![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]() dans
dans ![]() , on dit que
, on dit que ![]() est pôle d’ordre
est pôle d’ordre ![]() de
de ![]() .
.
![]() Si
Si ![]() , on dit que
, on dit que ![]() est un pôle simple.
est un pôle simple.
![]() Si
Si ![]() , on dit que
, on dit que ![]() est un pôle double.
est un pôle double.
1.3. Degré
![]() Soit
Soit ![]() .
.
![]() si
si ![]() , le degré de
, le degré de ![]() est défini par
est défini par ![]()
![]() si
si ![]() , on pose
, on pose ![]() .
.
![]() Si
Si ![]() et
et ![]() sont deux fractions rationnelles,
sont deux fractions rationnelles, ![]() .
.
1.4. Partie entière
![]() Soit
Soit ![]() , il existe
, il existe ![]() et
et ![]() uniques tels que
uniques tels que ![]() avec
avec ![]() .
.
![]() On dit que
On dit que ![]() est la partie entière de
est la partie entière de ![]() .
. ![]() est égal au quotient de la division euclidienne de
est égal au quotient de la division euclidienne de ![]() par
par ![]() .
.
![]()
![]() où
où ![]() est le reste de la division euclidienne de
est le reste de la division euclidienne de ![]() par
par ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2.Décomposition en éléments simples dans 
Soit ![]() une fraction irréductible non nulle à coefficients dans
une fraction irréductible non nulle à coefficients dans ![]() .
.
On décompose ![]() en produit de facteurs irréductibles dans
en produit de facteurs irréductibles dans ![]() :
: 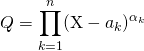 .
.
Il existe un unique ![]() et une unique famille de complexes
et une unique famille de complexes ![]()
tels que
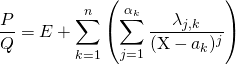
De plus 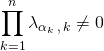 .
.
![]() est la partie entière de la fraction
est la partie entière de la fraction ![]() .
.
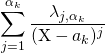 est la partie polaire relative au pôle
est la partie polaire relative au pôle ![]() .
.
h.p : ![]() est le résidu (d’ordre 1) du pôle
est le résidu (d’ordre 1) du pôle ![]() .
.
3. Décomposition en éléments simples dans 
Soit ![]() une fraction irréductible non nulle à coefficients dans
une fraction irréductible non nulle à coefficients dans ![]() .
.
On décompose ![]() en produit de facteurs irréductibles dans
en produit de facteurs irréductibles dans ![]() :
:
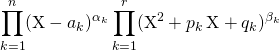
avec ![]() si
si ![]() .
.
Il existe un unique ![]() et trois uniques familles de réels
et trois uniques familles de réels ![]()
et ![]() tels que
tels que
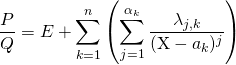
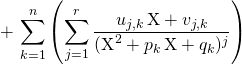 .
.
4. Méthodes de calcul
![]()
![]() est le quotient de la division euclidienne de
est le quotient de la division euclidienne de ![]() par
par ![]() , donc
, donc ![]() si
si ![]() .
.
![]() Si
Si ![]() est pôle simple de la fraction
est pôle simple de la fraction ![]() ,
,
la partie polaire relative à ![]() est
est ![]() avec
avec ![]() .
.
![]() Soit
Soit ![]() décomposée en éléments simples dans
décomposée en éléments simples dans ![]() .
.
Si ![]() est pôle d’ordre
est pôle d’ordre ![]() de la fraction
de la fraction ![]() , la partie polaire relative à
, la partie polaire relative à ![]() est la conjuguée de la partie polaire relative à
est la conjuguée de la partie polaire relative à ![]() .
.
![]() Si
Si ![]() est pôle d’ordre
est pôle d’ordre ![]() de la fraction irréductible
de la fraction irréductible ![]() , si
, si ![]() alors le terme
alors le terme ![]() se calcule par
se calcule par ![]() .
.
![]() Dans le cas d’une décomposition en éléments simples sans partie entière de la forme
Dans le cas d’une décomposition en éléments simples sans partie entière de la forme
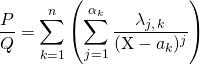 ,
,
on obtient 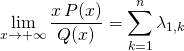
(on multiplie par ![]() et on passe à la limite en
et on passe à la limite en ![]() ).
).
![]() Dans le cas d’une fraction rationnelle de la forme
Dans le cas d’une fraction rationnelle de la forme ![]() dont les pôles non réels sont tous simples et qui a été décomposée en éléments simples dans
dont les pôles non réels sont tous simples et qui a été décomposée en éléments simples dans ![]() , pour obtenir la décomposition en éléments simples dans
, pour obtenir la décomposition en éléments simples dans ![]() , il suffit de regrouper les termes de la forme
, il suffit de regrouper les termes de la forme ![]() et de réduire au même dénominateur pour obtenir une expression de la forme
et de réduire au même dénominateur pour obtenir une expression de la forme ![]() avec
avec ![]() .
.
![]() On peut aussi évaluer la relation en un ou plusieurs points particuliers pour obtenir une ou plusieurs équations complémentaires lorsqu’il y a au moins un pôle multiple.
On peut aussi évaluer la relation en un ou plusieurs points particuliers pour obtenir une ou plusieurs équations complémentaires lorsqu’il y a au moins un pôle multiple.
5. Exemples classiques
Exemple 1
Si ![]() ,
, ![]() , décomposition en éléments simples de
, décomposition en éléments simples de ![]() dans
dans ![]()
Correction : C’est une fraction rationnelle irréducti-ble, sans partie entière dont les pôles sont tous simples et sont les complexes
![]() pour
pour ![]() .
.
On obtient une décomposition en éléments simples de la forme
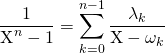
et on calcule ![]() .
.
![]()
donc ![]() , ce qui donne :
, ce qui donne :
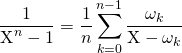 .
.
Exemple 2
Décomposition en éléments simples de ![]() dans
dans ![]() puis
puis ![]() .
.
Correction : ![]() Décomposition dans
Décomposition dans ![]() .
.
On écrit cette fois ci- les pôles sous la forme
![]() pour
pour ![]() .
.
et on remarque qu’il y a deux pôles réels 1 et ![]() obtenus pour
obtenus pour ![]() et
et ![]() .
.
De plus, le conjugué du pôle ![]() est
est ![]() .
.
Comme dans l’exemple précédent, la partie polaire relative au pôle ![]() est
est ![]() avec
avec ![]() et
et ![]() .
.
![]()
![]()
donc ![]() .
.
La décomposition dans ![]() est :
est :
![]()
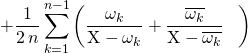 .
.
![]() Décomposition dans
Décomposition dans ![]() .
.
On simplifie ![]()
que l’on écrit sous la forme ![]()
avec ![]()
![]() car
car ![]()
![]()
et ![]()
![]()
![]()
donc
![]()
Retenir les notions directement en cours est souvent difficile compte tenu du rythme soutenu auquel se déroulent ces derniers. Nos cours en ligne et nos cours de soutien de maths vous permettent de revoir ces notions essentielles et de prendre le temps de les assimiler. Après avoir révisé ce cours sur les fractions rationnelles, consultez les notions clés des prochains chapitres à venir :

