Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours en ligne Maths en Maths Sup

Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours : Fonctions en Maths Sup MPSI, PTSI, PCSI, MP2I

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Maths Sup

Résumé de cours et méthodes – Fonctions Première partie en Maths Sup

Plan :

1 Manipuler les définitions de base
1.1. Définition et image.
1.2. Parité
1.3. Périodicité
1.4. Fonction majorée, minorée, bornée
1.5. Monotonie
1.6. Composition
1.7. Asymptote horizontale ou verticale

2. Dérivation
2.1. Définition
2.2. Utilisation des opérations
2.3. Dérivation et monotonie
2.4. Extremum d’une fonction réelle
2.5. Calcul pratique de dérivées
2.6. Dérivées successives

3. Fonction réelle bijective
3.1. Fonction réciproque
3.2. Dérivée d’une fonction réciproque

Toutes ces notions seront approfondies dans les chapitres continuité et dérivabilité. N’hésitez pas à compléter ces notions avec les cours de maths.

La deuxième partie de méthodes permet de bien rédiger l’étude d’une fonction. Elle est suivie de 2 exemples.

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

1. Manipuler les définitions de base

On note $\mathcal{R} (O , \overrightarrow{i} , \overrightarrow{j} )$ un repère du plan lorsque l’on manipule des fonctions réelles.
Pour une fonction $f$ à valeurs réelles définie sur $\mathcal{D}$ , on note $\Gamma$ l’ensemble des points $M(x) (x , f(x))$ lorsque $x \in \mathcal{D}$
et on trace le graphe $\Gamma$ de $f$ dans le repère $\mathcal{R}$ .

1.1. Définition et image $\mathcal{D}$ d’une fonction.
$\bullet$ S’assurer que la recherche du domaine de définition a été faite par CNS !
Un raisonnement comme celui qui suit ne répond pas à la question :
écrire $f(x)$ défini implique $x \in \mathcal {D'}$ donne seulement $\mathcal{D} \subset \mathcal{D'}$ .
Il est indispensable d’étudier l’inclusion réciproque.
Il est conseillé de raisonner lorsque c’est possible en mettant en évidence une équivalence.

$\bullet$ On définit alors l’image de $f$ :
$\quad \quad f(\mathcal{D}) = \{ f(x) \, , \, x \in \mathcal{D}\}$ .

$\bullet$ théorème des valeurs intermédiaires
Si $f$ est continue sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ , $f(I)$ est un intervalle de $\mathbb{R}$ ,
c’est à dire si $(a , b) \in I^2$ sont tels que $f(a) < f(b)$ , pour tout $k \in \; ]f(a) \, , \, f(b)[$ , il existe $x_0$ strictement compris entre $a$ et $b$ tel que $f(x_0) = k$ .

1.2. Parité
But : étudier la parité d’une fonction définie sur $\mathcal{D}$ .
$\ast$ S’assurer que $\mathcal{D}$ est centré en 0 c’est à dire que $x \in \mathcal{D} \Leftrightarrow - x \in \mathcal{D}$ .

$\ast$ Pour démontrer que $f$ est paire, démontrer alors que $\quad \forall \, x \in \mathcal{D} ,\, f(-x) = f(x)$ .
Dans ce cas, il suffit d’étudier la fonction $f$ sur $\mathcal{D} \cap \mathbb{R}^+$ et si $f$ est à valeurs réelles, son graphe est symétrique par rapport à $Oy$ .

$\ast$ Pour démontrer que $f$ est impaire, démontrer alors que $\quad \forall \, x \in \mathcal{D} ,\, f(-x) = - f(x)$ .
Dans ce cas, il suffit d’étudier la fonction $f$ sur $\mathcal{D} \cap \mathbb{R}^+$ et si $f$ est à valeurs réelles, son graphe est symétrique par rapport à $O$ .

1.3. Période
$\bullet$ Pour démontrer qu’une fonction $f$ est périodique sur $\mathcal{D}$ ,
Il suffit de trouver un réel $T > 0$ tel que $x \in \mathcal{D} \Rightarrow x + T \in \mathcal{D}$
et de démontrer que $\quad \quad \forall \, x \in \mathcal{D},\, f(x + T) = f(x)$
On dit alors que $T$ est une période de $f$ ou que $f$ est $T$ –périodique.

$\bullet$ Si $f$ est $T$ -périodique, il suffit de l’étudier sur un intervalle de longueur $T$ que l’on pourra choisir de la forme $[0 ,\, T] \cap \mathcal{D}$ ou $[- T/2 , \, T/2] \cap \mathcal{D}$ .

$\bullet$ Si $f$ est $T$ -périodique et réelle , le graphe de $f$ dans le repère $\mathcal{R}$ est invariant par translation de vecteur $T \overrightarrow{i}$ c’est à dire pour tout $x \in \mathcal{D}$ , $\quad \quad \overrightarrow{ M(x) M(x + T)} =T\, \overrightarrow { i}$ .

: Pour restreindre le domaine d’étude d’une fonction, toujours commencer par la périodicité, si elle est $T$ -périodique et si elle est paire ou impaire, se restreindre d’abord à $[- T/2\, , \, T/2] \cap \mathcal{D}$ .
Ce qui permet éventuellement de se restreindre ensuite à une étude sur $[0 , \, T/2] \cap \mathcal{D}$ .

1.4. Fonction majorée, minorée, bornée
à l’ordre des quantificateurs
Soit $f$ définie sur $\mathcal{D}$ à valeurs réelles.
$\ast$ $f$ est majorée ssi $\quad \exists \, M \in \mathbb{R}, \forall\, x \in \mathcal{D} , f(x) \leq M$ .
$\ast$ $f$ est minorée ssi $\quad \exists \, m \in \mathbb{R}, \forall\, x \in \mathcal{D} , f(x) \geq m$ .

Soit $f$ définie sur $\mathcal{D}$ à valeurs réelles ou complexes.
$\ast$ $f$ est bornée ssi $\quad \exists \, M \in \mathbb{R}, \forall\, x \in \mathcal{D} , \vert f(x) \vert \leq M$ .
: Si $f$ est à valeurs réelles, cela revient à dire que $f$ est majorée et minorée, mais cette écriture est plus concise et maniable en pratique.

1.5. Monotonie
$\bullet$ Définitions
Soit $f$ définie sur un intervalle $I$ à valeurs dans $\mathbb{R}$ .
$\ast$ $f$ est croissante sur $I$ ssi
$\forall \, (x ,\, y) \in I^2,\, (x < y \Rightarrow f(x) \leq f(y))$ .

$\ast$ $f$ est décroissante sur $I$ ssi
$\forall \, (x ,\, y) \in I^2,\, (x < y \Rightarrow f(x) \geq f(y))$ .

$\ast$ $f$ est strictement croissante sur $I$ ssi
$\forall \, (x ,\, y) \in I^2,\, (x < y \Rightarrow f(x) < f(y))$ .

$\ast$ $f$ est strictement décroissante sur $I$ ssi
$\forall \, (x ,\, y) \in I^2,\, (x < y \Rightarrow f(x) > f(y))$ .

Elle est monotone (resp. strictement monotone) sur $I$ ssi elle est croissante ou décroissante (resp. strictement croissante ou strictement décroissan- te) sur $I$ .

$\bullet$ Somme de deux fonctions de même monotonie.
Si $f$ et $g$ sont deux fonctions
… croissantes (resp. strictement croissantes) sur $\mathcal{D}$ , $f + g$ est croissan- te (resp. strictement croissante) sur $\mathcal{D}$ .
… décroissantes (resp. strictement dé- croissantes) sur $\mathcal{D}$ , $f + g$ est décrois- sante (resp. strictement décroissante) sur $\mathcal{D}$ .

aux produits de fonctions monotones ou strictement monotones il est indispensable de vérifier qu’elles sont de signe constant et d’effectuer proprement le produit des inégalités.

1.6. Composition
$\bullet$ Soient $f$ définie sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ , $g$ définie sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ et on suppose que $f(I) \subset J$ .
$\ast$ Si $f$ et $g$ sont monotones (resp. strictement monotones) de même sens de variation, $g \circ f$ est croissante (resp. strictement croissante) sur $I$

$\ast$ Si $f$ et $g$ sont monotones (resp. strictement monotones) de sens contraires, $g \circ f$ est décroissante (resp. strictement décroissante) sur $I$ .

1.7. Asymptote horizontale ou verticale
$f : I \to \mathbb{R}$ et $\Gamma$ sa représentation graphique.
Soit $a \in \mathbb{R}$
$\bullet$ si $\displaystyle \lim_{x \to \infty} f(x) = a$ , la droite d’équation $y = a$ est asymptote à $\Gamma$ .
$\bullet$ si $\displaystyle \lim_{x \to a} f(x) = \infty$ , la droite d’équation $x = a$ est asymptote à $\Gamma$ .

2. Dérivation

On note $\mathbb{K} = \mathbb{R}$ ou $\mathbb{C}$ .
2.1. Définition
$\bullet$ $f$ définie sur $\mathcal{D}$ à valeurs dans $\mathbb{K}$ ,
et $a \in \mathcal{D}$ est dérivable en $a$ lorsque $x \mapsto \displaystyle \frac {f(x) - f(a)} {x - a}$ admet une limite finie $L$ en $a$ .
On note $L = f'(a)$ .
Elle est dérivable sur $\mathcal{D}$ lorsqu’elle est dérivable en tout point de $\mathcal{D}$ .

$\bullet$ Tangente
Soit $f$ une fonction définie sur $\mathcal{D}$ à valeurs dans $\mathbb {R}$ , dérivable en $a \in \mathcal{D}$ .
Le graphe de $f$ admet une tangente en $(a ,\, f(a))$ d’équation
$\quad \quad y - f(a) = f'(a) (x - a)$ .

$\bullet$ Tangente verticale
Soit $f$ une fonction définie sur $\mathcal{D}$ à valeurs dans $\mathbb {R}$ , continue en $a \in \mathcal{D}$ .
lorsque $\displaystyle \lim_{x \to a} \frac {f(x) - f(a)} {x - a}= \infty$ ,
Le graphe de $f$ admet une tangente verticale en $(a ,\, f(a))$ .

2.2. Utilisation des opérations
$f$ et $g$ des fonctions définies sur $\mathcal{D}$ à valeurs dans $\mathbb{K}$ , et $a \in \mathcal{D}$ .
$\bullet$ Si $\alpha$ et $\beta$ sont éléments de $\mathbb{K}$ , si $f$ et $g$ sont dérivables en $a$ (resp. sur $\mathcal{D}$ ),
$\alpha f + \beta\, g$ est dérivable en $a$ (resp. sur $\mathcal{D}$ )
et $(\alpha f + \beta \, g) '(a) = \alpha f ' (a) + \beta \, g'(a)$
(resp $(\alpha f + \beta\, g) = \alpha\, f' + \beta\, g'$ ).

$\bullet$ Si $f$ et $g$ sont dérivables en $a$ (resp. sur $\mathcal{D}$ ), $f \, g$ est dérivable en $a$ (resp sur $\mathcal{D}$ )
et $( f \, g) '(a) = f ' (a)\, g(a) + f(a) \,g'(a)$
(resp $( f \, g) '= f ' \, g + f \,g'$ ).

$\bullet$ Si $f$ et $g$ sont dérivables en $a$ (resp. sur $\mathcal{D}$ ) et si $g$ ne s’annule pas sur $\mathcal{D}$ ,
$\displaystyle \frac f g$ est dérivable en $a$ (resp. sur $\mathcal{D}$ )
et $\displaystyle \left ( \frac f g \right ) '(a) = \frac { f ' (a)\, g(a) - f(a) \,g'(a)} {g(a) ^2}$
(resp $\displaystyle \left ( \frac f g \right ) ' = \frac { f '\, - f \,g'} {g ^2}$ ).

$\bullet$ Pour les fonctions à valeurs complexes
Soit $f$ une fonction définie sur $\mathcal{D}$ à valeurs dans $\mathbb{C}$ et $a \in \mathcal{D}$ .
On écrit pour tout $x \in \mathcal{D}$ , $\quad \quad \quad \, f(x) = g(x) + \textrm{i} \, h(x)$
où $g$ et $h$ sont à valeurs réelles.
$f$ est dérivable en $a$ (resp. sur $\mathcal{D}$ )
ssi $g$ et $h$ sont dérivables en $a$ (resp. sur $\mathcal{D}$ ) et $f'(a) = g'(a) + \textrm{i} \, h'(a)$
(resp. $f'= g'+ \textrm{i} \, h'$ ).

$\bullet$ Par utilisation d’une composition
On suppose que $f : \mathcal{D} \to \mathbb{R}$ , $g : \mathcal{D'} \to \mathbb {K}$ et $f(\mathcal{D} ) \subset \mathcal{D'}$ .
$\ast$ Si $f$ est dérivable en $a$ , si $g$ est dérivable en $b = f(a)$ , $g \circ f$ est dérivable en $a$ et
$\quad \quad (g \circ f)'(a) = f'(a) \, g'(f(a))$ .
$\ast$ si $f$ est dérivable sur $\mathcal{D}$ , si $g$ est dérivable sur $\mathcal{D}'$ , $g \circ f$ est dérivable sur $\mathcal{D}$ et $(g \circ f)' = f' \, g'\circ f$ .

$\bullet$ Si $\varphi$ est une fonction dérivable sur $\mathcal{D}$ à valeurs dans $\mathbb{C}$ , $g : t \mapsto \textrm{exp} (\varphi(t))$
est dérivable sur $\mathcal{D}$ et $\quad \forall\, t \in \mathcal{D}, g'(t) = \varphi'(t) \, \textrm{exp} (\varphi(t))$ .

2.3. Dérivation et monotonie
$\bullet$ Soit $f$ une fonction dérivable sur l’intervalle $I$ à valeurs dans $\mathbb{R}$
$f$ est constante sur $I$ ssi $\quad \quad \forall \, x \in I,\, f'(x) = 0$ .
Remarque : la propriété reste vraie si $f$ est à valeurs dans $\mathbb{C}$ .

$\bullet$ Soit $f$ une fonction continue sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ et dérivable sur $J = \overset {\circ } I$ , intervalle de $I$ privé de ses bornes.
$\ast$ $f$ est croissante sur $I$
ssi $\forall \, x \in J,\, f'(x) \geq 0$ .
$\ast$ $f$ est décroissante sur $I$
ssi $\forall \, x \in J,\, f'(x) \leq 0$ .

$\bullet$ Soit $f$ une fonction continue sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ et dérivable sur $J = \overtset {\circ} I$ , intervalle de $I$ privé de ses bornes.
$\ast$ $f$ est strictement croissante sur $I$
ssi $\forall \, x \in J,\, f'(x) \geq 0$ et si $f'$ ne s’annule sur aucun segment $[a, b]$ où $a , \,b$ sont éléments de $J$ tels que $a < b$
$\ast$ $f$ est strictement décroissante sur $I$ ssi $\forall \, x \in J,\, f'(x) \geq 0$ et si $f'$ ne s’annule sur aucun segment $[a, b]$ où $a , \, b$ sont éléments de $J$ tels que $a < b$
Conséquences :
Soit $f$ une fonction continue sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ et dérivable sur $J$ , intervalle de $I$ privé de ses bornes.
$\ast$ Si pour tout $x \in J, f'(x) > 0$ , $f$ est strictement croissante sur $I$ .
$\ast$ Si pour tout $x \in J, f'(x) < 0$ , $f$ est strictement décroissante sur $I$ .

: Pour étudier le sens de variation d’une fonction $f$ dérivable :
$\ast$ On calcule si $x \in I,\, f'(x)$ .
$\ast$ On résout l’inéquation $f'(x) > 0$ .
Résoudre $f'(x) = 0$ ne donne pas le signe de $f'(x)$ !

2.4. Extremum d’une fonction réelle
$\bullet$ $f$ définie sur $I$ à valeurs dans $\mathbb{R}$ ,
$\ast$ $f$ admet un maximum sur $I$ s’il existe $a\in I$ tel que $\forall \, x \in I, f(x) \leq f(a)$ .
$\ast$ $f$ admet un minimum sur $I$ s’il existe $a\in I$ tel que $\forall \, x \in I, f(x) \geq f(a)$ .
$\ast$ $f$ admet un extremum sur $I$ si $f$ admet un minimum ou un maximum sur $I$ .

$\bullet$ $f$ définie sur $I$ à valeurs dans $\mathbb{R}$ ,
$\ast$ $f$ admet un maximum local en $a \in I$ s’il existe $\alpha > 0$ tel que $\forall \, x \in I \; \cap\; ]a - \alpha , a + \alpha[,\, f(x) \leq f(a)$ .
$\ast$ $f$ admet un minimum local en $a \in I$ s’il existe $\alpha > 0$ tel que $\forall \, x \in I\; \cap \; ]a - \alpha , a + \alpha[,\, f(x) \geq f(a)$ .
$\ast$ $f$ admet un extremum local en $a \in$ si $f$ admet un minimum ou un maximum local en $a \in I$ .

$\bullet$ Si $f$ définie sur $I$ à valeurs dans $\mathbb{R}$ et admet un extremum local en $a\in I$ , différent des bornes et est dérivable en $a$ , $f'(a) = 0$ .
La réciproque est fausse : prendre $f : x \mapsto x^3$ sans extremum local en $0$ alors que $f'(0) = 0$ .

Sous les hypothèses précédentes, si $f'$ s’annule en $a$ et change de signe en $a$ , $f$ admet un extremum local en $a$ .

Si $f = \displaystyle \frac u v$ est telle que $f'(\alpha) = 0$ avec $v(\alpha)\, v'\alpha) \neq 0$ , $f(\alpha) = \displaystyle \frac {u'(\alpha)} {v'(\alpha)}$ .

Démonstration : En effet $f' = \displaystyle \frac {u' \, v - u \, v'} {v ^2}$ .
Comme $f'(\alpha) = 0$ , $\quad \quad u'(\alpha) \, v(\alpha) - u(\alpha) \, v'(\alpha) = 0$ ,
en divisant par $v(\alpha)\, v'\alpha) \neq 0$ ,
$\quad \quad \quad \displaystyle \frac {u(\alpha)} {v(\alpha)}= \frac {u'(\alpha)} {v'(\alpha)}$ .

2.5. Calcul pratique de dérivées
$\bullet$ Notation
Important : Il faut essayer de ne plus être obligé d’écrire les formules de dérivation utilisées.
Si vous ne pouvez pas vous en empêcher, il faut prendre la précaution d’écrire par exemple $(u \, v) ' = u' \, v + u \, v'$
ou $(u \, v) ' (x) = u' (x) \, v(x) + u (x) \, v'(x)$
mais JAMAIS $(u (x) \, v(x)) ' = u'(x) \, v(x) + u (x) \, v' (x)$
car on dérive une fonction et non un réel !

Des astuces dans les points suivants :
$\bullet$ Pour aller plus vite :
$\ast$ si $(a , b , c , d) \in \mathbb{R}^4$ et $f : x \displaystyle \mapsto \frac {a \, x + b} {c \, x + d}$
en tout point où $f$ est définie, $\quad \quad f '(x) = \displaystyle \frac {a \, d - b \, c} {(c \, x + d)^2 }$ .

$\ast$ Pour dériver $\displaystyle \frac 1 {u ^n}$ où $n \in \mathbb{R}$ , il est plus simple d’écrire : $v = u ^{- n}$ puis $v' = - n \, u' \, u ^{ - n - 1}$ $\Rightarrow$ $\displaystyle \left ( \frac 1 {u ^n} \right )' = \frac {n \, u'} {u ^{n + 1} }$
Il est très maladroit d’utiliser la dérivée d’un quotient !

$\ast$ Pour dériver $\displaystyle \frac u {v ^n}$ où $n \in \mathbb{R}$ , il est plus simple d’écrire : $w = u \, v ^{- n}$ et d’utiliser la dérivée d’un produit
$\quad \quad w' = u \, v ^{- n} - n\, u \, v' \, v ^{ - n - 1}$
de réduire ensuite au même dénomi- nateur
donc $\displaystyle \left ( \frac u {v ^n} \right )' = \frac {u' \, v - n \,u \, v' } {v ^{n + 1} }$ .
Pour ce calcul, il est très-très maladroit d’utiliser la dérivée d’un quotient !
Il faut retenir que par dérivation, le « degré » du dénominateur n’augmente que d’une unité et ne double que si $n = 1$ .

$\ast$ Pour dériver $\displaystyle \frac {u \, v} {w}$ , il est plus simple d’écrire $\displaystyle u \, v \, \frac 1 w$ et de dériver sous la forme d’un produit
$(u \, v \, (1 / w) )' =$ $\quad \quad u' \, v \, w ^{- 1} + u \, v' \, w ^{- 1} - u \, v \, w' \, w ^{- 2}$
et de réduire ensuite au même dénominateur.

2.6. Dérivées successives
$\bullet$ Si $f : I \to \mathbb{K}$ , on définit sous réserve d’existence $f^{(n)}$ par
$f^{(0)} = f$ , $f^{(1)} = f'$ et $f^{(n+1 )} = (f^{(n)})'$ .

$\bullet$ Dérivées successives à savoir calculer rapidement
$\ast$ si $n \in \mathbb{N}$ et $a \in \mathbb{C}$ , $u : x \mapsto (x - a) ^n$
… si $p \leq n$ , $\quad u ^{(p)}(x) = \displaystyle \frac {n!} {(n - p)!} (x - a)^{n - p}$
… si $p >n$ , $u ^{(p)}(x) = 0$ .

$\ast$ si $a \in \mathbb{C}$ et $u : x \mapsto \displaystyle \frac 1 {x - a}$
si $n \in \mathbb{N} ^*$ , $u ^{(n)}(x) = \displaystyle \frac {n!\, (-1) ^n } {(x - a) ^{n + 1}} .$

$\ast$ si $a \in \mathbb{C}$ et $u : x \mapsto \displaystyle \frac 1 {a - x}$ ,
si $n \in \mathbb{N} ^*$ , $u ^{(n)}(x) = \displaystyle \frac {n!} {(a - x) ^{n + 1}}$ .

$\bullet$ Utiliser les théorèmes de dérivation. Soit $n \in \mathbb{N}^*$ .
Si $u$ et $v$ sont $n$ fois dérivables sur $I$ , il en est de même de toute combinaison linéaire, du produit, du quotient $u/v$ si $v$ ne s’annule pas, de la composée $u \circ v$ sous réserve de sa définition.
Vous verrez plus tard la formule de Leibniz :
$\quad (u \, v) ^{(n)} = \displaystyle \sum _ {k = 0} ^n \binom n k u^{(k)} \, v^{(n - k)}$ .

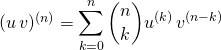UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

3. Fonction réelle bijective

3.1. Fonction réciproque
$\bullet$ Soit $f$ une fonction strictement monotone sur l’intervalle $I$ , $f$ définit une bijection de $I$ sur $f(I)$ .
c’est à dire
$\quad \forall \, y \in f(I), \, \exists \, ! \, \in I, \, y = f(x)$ .
La fonction $f$ admet une fonction réciproque $g = f ^{ - 1} : \, f(I) \to I$ strictement monotone de même sens de variation que $f$ .

: Les graphes de $f$ et $g$ sont symétriques par rapport à la droite d’équation $y = x$ .

$\bullet$ Théorème (souvent appelé théorème de la bijection)
Soit $f$ une fonction continue et strictement monotone sur l’intervalle $I$ , $f$ définit une bijection de $I$ sur $f(I)$ sa fonction réciproque est continue et strictement monotone sur $f(I)$ , de même sens de variation que $f$ .

Comment déterminer $f(I)$ lorsque $f$ est continue sur $I$ ?
$\ast$ $I = [a \, , \, b]$
… $f(I) = [f(a) \, , \, f(b)]$ si $f$ est strictement croissante.
… $f(I) = [f(b) \, , \, f(a)]$ si $f$ est strictement décroissante.

$\ast$ $I = [a \, , \, b[$
… $\displaystyle f(I) = \left [f(a) \, , \, \lim_{x \to b} f(x) \right [$ si $f$ est strictement croissante.
… $\displaystyle f(I) = \left ]\lim_{x \to b} f(x) \, , \, f(a)\right ]$ si $f$ est strictement décroissante.

Je vous laisse adapter dans le cas où $I =\; ]a , b]$ .

$\ast$ $I = ]a \, , \, b[$
… $\displaystyle f(I) = \left ]\lim_{x \to a} f(x) \, , \, \lim_{x \to b} f(x) \right [$ si $f$ est strictement croissante.
… $\displaystyle f(I) = \left ]\lim_{x \to b} f(x) \, , \, \lim_{x \to a} f(x) \right ]$ si $f$ est strictement décroissante.

à ne pas confondre la fonction réciproque $f ^{- 1}$ de $f$ lorsqu’elle existe et la fonction inverse $\displaystyle \frac 1 f$ lorsqu’on peut la définir.

3.2. Dérivée de la fonction réciproque
$\bullet$ Version 1
Soit $f$ une fonction continue sur l’intervalle $I$ à valeurs dans $R$ .
Si $f$ est dérivable sur $I$ et si $\quad \quad \forall\, x \in J,\, f'(x) \neq 0$ ,
$\ast$ $f$ définit une bijection de $I$ sur $f (I)$
$\ast$ $f ^{- 1}$ est dérivable sur $f(I)$ .
$\forall \, y \in f(I)$ , $(f ^{- 1})'(y) = \displaystyle \frac 1 {f ' (f ^{-1}(y))}$ .

$\bullet$ Version 2
Soit $f$ une fonction continue sur l’intervalle $I$ à valeurs dans $R$ .
On note $J$ l’intervalle $I$ privé de ses bornes.
Si $f$ est dérivable sur $J$ et si $\quad \quad \forall\, x \in J,\, f'(x) \neq 0$ ,
$\ast$ $f$ définit une bijection de $I$ sur $f (I)$
$\ast$ $f ^{- 1}$ est dérivable sur $f(J)$ .
$\forall \, y \in f(J)$ , $(f ^{- 1})'(y) = \displaystyle \frac 1 {f ' (f ^{-1}(y))}$ .

Préparez la suite de l’année de Maths Sup grâce aux prochains chapitres de mathématiques de MPSI, PTSI et PCSI :

Cours : Fonctions en Maths Sup MPSI, PTSI, PCSI, MP2I

Résumé de cours et méthodes – Fonctions Première partie en Maths Sup

Plan :

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

1. Manipuler les définitions de base

2. Dérivation

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

3. Fonction réelle bijective

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Cours : Fonctions en Maths Sup MPSI, PTSI, PCSI, MP2I

Résumé de cours et méthodes – Fonctions Première partie en Maths Sup

Plan :

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

1. Manipuler les définitions de base

2. Dérivation

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension clés de la réussite

Cours de maths en ligne ou à domicile

3. Fonction réelle bijective

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

La pratique et la compréhension
clés de la réussite