Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Les Matrices, cours de Maths Sup MPSI, MP2I, PCSI, PTSI
Découvrez avec ce cours en ligne en Maths Sup, un cours complet sur le chapitre des matrices. Un chapitre important dans le programme de maths en Maths Sup, mais un chapitre également très important pour obtenir de bons résultats aux concours post-prépa pour intégrer les écoles d’ingénieurs les plus réputées de France. Beaucoup d’étudiants en maths sup recherchent un prof de maths à domicile pour maîtriser les matrices et bien plus.
A. Matrices de type  à coefficients dans
à coefficients dans  .
.
On suppose que ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() .
.
1. Définitions des matrices en Maths Sup
Soient ![]() et
et ![]() ,
,
avec ![]()
et ![]() .
.
![]()
![]() est définie par
est définie par
![]()
où si ![]() et
et ![]() ,
,![]() .
.
![]() Si
Si ![]() ,
, ![]() est définie par
est définie par ![]()
où si ![]() et
et ![]() ,
,
![]() .
.
Lorsque ![]() , l’ensemble
, l’ensemble ![]() est noté
est noté ![]() .
.
2. Propriétés de matrices en Maths Sup
P1 : ![]() est un
est un ![]() –espace vectoriel.
–espace vectoriel.
P2 : Si ![]() ,
,
on définit ![]()
par ![]()
i.e. tous les éléments de ![]() sont nuls sauf celui situé en ligne
sont nuls sauf celui situé en ligne ![]() et colonne
et colonne ![]() qui est égal à 1.
qui est égal à 1.
On note ![]() .
.
La famille ![]() est une base de
est une base de ![]() , appelée base canonique de
, appelée base canonique de ![]() .
.
![]() .
.
P3 : Décomposition de ![]() :
:
![]()
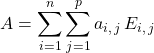 .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
B. Produit matriciel en Maths Sup
1. Définition du produit matriciel en Maths Sup
Si ![]() et
et ![]() ,
,
où ![]()
et ![]() ,
,
on définit ![]()
par ![]()
où si ![]() et
et ![]() ,
,
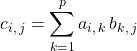 .
.
2. Produit d’une matrice de type  par une matrice colonne
par une matrice colonne
![]() ,
, ![]()
![]() ,
, ![]()
alors ![]() ,
, ![]()
si ![]() ,
, 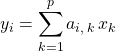 .
.
3. Propriétés d’un prpduit matriciel
Si les produits et sommes sont définis, et si ![]() ,
,



 .
.
C. Cas des matrices carrées d’ordre  en Maths Sup
en Maths Sup
1. Définitions des matrices carrées d’ordre 
Si ![]() ,
,
a) les éléments ![]() forment la diagonale de
forment la diagonale de ![]() . On dit que ce sont les éléments diagonaux de
. On dit que ce sont les éléments diagonaux de ![]() .
.
b) ![]() est dite diagonale lorsque
est dite diagonale lorsque
![]() .
.
c) ![]() est dite triangulaire supérieure lorsque
est dite triangulaire supérieure lorsque ![]() tels que
tels que ![]() .
.
d) ![]() est dite triangulaire inférieure lorsque
est dite triangulaire inférieure lorsque ![]() tels que
tels que ![]() .
.
e) ![]() est dite triangulaire si elle est triangulaire supérieure ou inférieure.
est dite triangulaire si elle est triangulaire supérieure ou inférieure.
2. Propriétés du produit matriciel en Maths Sup
Le produit matriciel dans ![]() s’écrit :
s’écrit :
si ![]() et
et ![]() ,
,
![]() est défini et
est défini et ![]() .
.
Si ![]() et
et ![]() ,
,
![]()
où ![]() ,
,
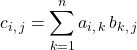 .
.
D : On définit la matrice unité d’ordre ![]()
![]() par
par ![]() .
.
Rappel : ![]()
P1 : ![]() est un anneau.
est un anneau.
Si ![]() ,
,
- associativité de la multiplication

- distributivité de la multiplication


- la matrice
 est élément neutre pour la multiplication :
est élément neutre pour la multiplication : 
 .
.
P2 : Si ![]() ,
, ![]() .
.
Si ![]() ,
, ![]() .
.
3. Puissance  -ième d’une matrice carrée
-ième d’une matrice carrée
D : Si ![]() , on définit par récurrence :
, on définit par récurrence :
![]() et si
et si ![]() .
.
(si ![]() , on démontre que
, on démontre que ![]() est le produit de
est le produit de ![]() matrices
matrices ![]() .)
.)
Formule du binôme de Newton.
Si ![]() vérifie
vérifie ![]() , pour tout
, pour tout ![]() ,
,
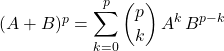 .
.
4. Base canonique de 
D : Si ![]() , on définit
, on définit
![]() par
par ![]()
i.e. tous les éléments de ![]() sont nuls sauf celui situé en ligne
sont nuls sauf celui situé en ligne ![]() et colonne
et colonne ![]() qui est égal à 1.
qui est égal à 1.
P1 : On note ![]() .
.
La famille ![]() est une base, dite base canonique, de
est une base, dite base canonique, de ![]() .
.
![]() .
.
P2 : Décomposition de ![]() :
:
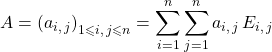 .
.
P3 : Produit de deux éléments de la base canonique.
Si ![]() ,
,
![]() .
.
5. Sous-espaces vectoriels particuliers en Maths Sup
P1 : L’ensemble ![]() des matrices carrées d’ordre
des matrices carrées d’ordre ![]() diagonales à coefficients dans
diagonales à coefficients dans ![]() est un s.e.v de
est un s.e.v de ![]() de dimension
de dimension ![]() . Il est stable par produit.
. Il est stable par produit.
P2 : L’ensemble ![]() des matrices carrées d’ordre
des matrices carrées d’ordre ![]() triangulaires supérieures à coefficients dans
triangulaires supérieures à coefficients dans ![]() est un s.e.v de
est un s.e.v de ![]() de dimension
de dimension ![]() . Il est stable par produit.
. Il est stable par produit.
P3 : Il en est de même de l’ensemble ![]() des matrices carrées d’ordre
des matrices carrées d’ordre ![]() triangulaires inférieures à coefficients dans
triangulaires inférieures à coefficients dans ![]() .
.
6. Matrices inversibles en Maths Sup
P : On note ![]() l’ensemble des matrices carrées d’ordre
l’ensemble des matrices carrées d’ordre ![]() à coefficients dans
à coefficients dans ![]() inversibles.
inversibles.
![]() est un groupe appelé groupe linéaire d’ordre
est un groupe appelé groupe linéaire d’ordre ![]() à coefficients dans
à coefficients dans ![]() .
.
 et son inverse est
et son inverse est  .
.- Si
 ,
,  et
et  .
. - Si
 ,
,  et son inverse est égal à
et son inverse est égal à  .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
D. Matrices et applications linéaires
1. Matrice d’une famille de vecteurs
Soit ![]() un
un ![]() -espace vectoriel de base
-espace vectoriel de base ![]() .
.
Soit ![]() une famille de
une famille de ![]() .
.
La matrice de la famille ![]() dans la base
dans la base ![]() est la matrice
est la matrice ![]() de type
de type ![]() telle que pour tout
telle que pour tout ![]() , la
, la ![]() -ème colonne de
-ème colonne de ![]() est formée des coordonnées de
est formée des coordonnées de ![]() dans la base
dans la base ![]() .
.
2. Matrice de 
D1 : La matrice de ![]() dans les bases
dans les bases ![]() de
de ![]() et
et ![]() de
de ![]() est une matrice notée
est une matrice notée
![]() ou
ou ![]()
de type ![]()
![]() où
où
![]() ,
, ![]() .
.
Pour retenir : Les coordonnées de ![]() dans la base
dans la base ![]() forment la
forment la ![]() -ème colonne de
-ème colonne de ![]() .
.
P1 : L’application
![]() ,
, ![]()
est un isomorphisme d’espaces vectoriels.
![]() .
.
3. Matrice d’un endomorphisme
D2 : La matrice de ![]() dans la base
dans la base ![]() de
de ![]() est une matrice carrée d’ordre
est une matrice carrée d’ordre ![]() où
où ![]() que l’on note
que l’on note ![]() ou
ou ![]() .
.
![]() avec
avec
![]() ,
, ![]() .
.
Pour retenir : Les coordonnées de ![]() dans la base
dans la base ![]() forment la
forment la ![]() -ème colonne de
-ème colonne de ![]() .
.
P2 : L’application
![]() ,
, ![]()
est un isomorphisme d’espaces vectoriels.
![]()
4. Application linéaire canonique- ment associée à 
D3 : C’est l’unique application linéaire ![]() dont la matrice dans les bases canoniques
dont la matrice dans les bases canoniques
![]() de
de ![]() et
et ![]() de
de ![]() est égale à
est égale à ![]() ,
,
soit ![]() ,
, ![]() .
.
5. Endomorphisme canoniquement associé à 
D4 : C’est l’unique endomorphisme ![]() dont la matrice dans la base canonique
dont la matrice dans la base canonique
![]() de
de ![]() est égale à
est égale à ![]() ,
,
soit ![]() ,
, ![]() .
.
6. Produit matriciel et applications linéaires
Soient ![]() ,
, ![]() et
et ![]() trois
trois ![]() -espaces vectoriels de bases respectives
-espaces vectoriels de bases respectives ![]() ,
, ![]() ,
, ![]() .
.
P4 : Si ![]() et
et ![]() ,
,
![]()
soit ![]() .
.
P5 : Si ![]() et si
et si ![]() ,
,
![]()
soit ![]() .
.
P6 : Si ![]() et
et ![]() ,
,
![]() .
.
P7 : Si ![]() ,
,
![]() .
.
7. Noyau, image et rang d’une matrice
D5 : Soient ![]() et
et ![]() l’application linéaire canoniquement associée à
l’application linéaire canoniquement associée à ![]() .
.
- On appelle noyau de la matrice
 le noyau de
le noyau de  , c’est donc un sev de
, c’est donc un sev de  . On le note
. On le note  .
. - On appelle image de
 l’image de
l’image de  . C’est donc un sev de
. C’est donc un sev de  .
.
On le note .
.
D6 : Soient ![]() et
et ![]() l’application linéaire canoniquement associée à
l’application linéaire canoniquement associée à ![]() .
.
On appelle rang de ![]() le rang de
le rang de ![]() .
.
C’est le nombre maximal de vecteurs colonnes de ![]() formant une famille libre. On le note
formant une famille libre. On le note ![]() .
.
P8 : Soit ![]() .
.
![]() si
si ![]() ,
,
![]()
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() ,
, ![]() .
.
P9 : Soit ![]() un
un ![]() -ev de base
-ev de base ![]()
Le rang de la famille ![]() de
de ![]() est le rang de la matrice
est le rang de la matrice ![]() de
de ![]() dans la base
dans la base ![]() .
.
P10 : Soient ![]() et
et ![]() sa matrice dans les bases
sa matrice dans les bases ![]() et
et ![]() ,
, ![]() .
.
8. Compléments sur les matrices inversibles
T1 : Soit ![]() .
.
Il y a équivalence entre
1. ![]() est inversible.
est inversible.
2. ![]()
3. L’endomorphisme ![]() canoniquement associé à
canoniquement associé à ![]() est un automorphisme
est un automorphisme
4. Pour tout ![]() de matrice
de matrice ![]() dans des bases
dans des bases ![]() et
et ![]() ,
, ![]() est un isomorphisme de
est un isomorphisme de ![]() sur
sur ![]() .
.
5. ![]()
6. ![]() telle que
telle que ![]()
7. ![]() telle que
telle que ![]()
Dans ce cas ![]() .
.
P11 : Soit ![]() une matrice triangulaire.
une matrice triangulaire.
![]() est inversible ssi le produit des termes diagonaux de
est inversible ssi le produit des termes diagonaux de ![]() est non nul.
est non nul.
L’inverse d’une matrice triangulaire supérieure (resp. inférieure) est triangulaire supérieure (resp. inférieure).
Les épreuves de mathématiques sont les épreuves de concours avec le coefficient le plus élevé. Les impasses sur les chapitres de maths en Maths Sup sont donc à proscrire. Pour se rendre compte de l’importance des mathématiques dans chaque concours, il est possible de consulter le simulateur d’admissibilité aux concours CPGE. Utiliser les cours en ligne et exercices corrigés de Maths Sup est une bonne solution pour préparer sa rentrée en Maths Spé. Quelques exemples de cours à bien travailler :

