Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours en ligne Maths en Maths Sup

Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours : Nombres réels en Maths Sup MPSI, PTSI, MP2I et PCSI

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Maths Sup

Résumé de cours et méthodes – Nombres réels en Maths Sup

Plan :

1. Équation et inéquation du second degré
2. Quelques conseils et recommanda- tions pour les inégalités
3. Pour démontrer une inégalité du type $u(x) \leq v(x)$
4. Utilisation de valeurs absolues
5. Parties majorées, minorées, bornées
6. Utiliser la partie entière
7. Intervalles de $\mathbb{R}$ .

Si vous ressentez le besoin, ne manquez pas de demander l’assistance d’un professeur particulier de maths.

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

1. équation et inéquation du second degré

Dans la suite, on note $\quad \quad P(x) = a \, x^2 + b \, x + c$
où $(a , b , c) \in \mathbb{R}^* \times \mathbb{R}^2$ .

$\bullet$ 🧡 Si $P$ admet deux racines réelles $x_1$ et $x_2\,$ ,
$\quad \displaystyle x_1 + x_2 = - \frac {b} a$ et $\displaystyle x_1 \, x_2 = \frac {c} a$ .

$\bullet$ Pour déterminer $u$ et $v$ réels dont on connaît la somme $S = u + v$ et le produit $P = u \, v$ , on écrit que $u$ et $v$ sont racines de l’équation $\quad \quad x ^2 - S \, x + P = 0$ .
Le problème a une solution ssi $S^2 - 4 \, P \geq 0$ .

$\bullet$ 👍 pas de précipitation dans la recherche des racines de $P$ !
$\ast$ Prendre le temps de chercher si $1$ ou $-1$ n’est pas racine de $P$ .
$\ast$ Si $P(1) = 0$ , l’autre racine est égale à $\displaystyle \frac c a$ .
$\ast$ Si $P(- 1) = 0$ , l’autre racine est égale à $\displaystyle - \frac c a$ .
Dans les deux cas, on détermine l’autre racine en utilisant : $\displaystyle \frac c a$ est le produit des racines.
$\ast$ Ne passez pas à côté d’une identité remarquable :
$\quad \quad x ^2 - 2 \, d \, x + d^2 = (x - d) ^2$ .

$\bullet$ Si l’on connaît les racines $x_1$ et $x_2$ de $P$ où $P(x) = a \, x^2 + b \, x + c$ , on peut factoriser $P(x)$ : $\quad \quad P(x) = a(x - x_1)(x - x_2)$
⚠️ à ne pas oublier le coefficient $a$ !

$\bullet$ Signe de $P(x) = a \, x^2 + b \, x + c$ .
$\ast$ Si $\Delta < 0$ , pour tout réel $x$ , $P(x)$ est du signe de $a$ .
$\ast$ Si $\Delta = 0$ , pour tout réel $x$ , $P(x)$ est du signe de $a$ et non nul si $x \neq \displaystyle \frac {- b} {2\, a}$ .
$\ast$ Si $\Delta > 0$ , $P$ a deux racines distinctes $x_1 < x_2 \,$ ,
sur $]x_1 \, , \, x_2[$ , $P(x)$ est du signe de $- a$
sur $]-\infty \, , x_1| \, \cup \, ]x_2 \, , \, +\infty[$ , $P(x)$ est du signe de $a$ .

$\bullet$ Pour placer un réel $t$ par rapport aux racines $x_1 < x_2$ de $P$ avec $\quad \quad P(x) = a \, x^2 + b \, x + c$ .
$\ast$ Calculer $P(t)$ .
$\ast$ Si $a \,P(t) <0$ , $x_1 < t < x_2\,$ .
$\ast$ Si $a \,P(t) > 0$ , $t$ est à l’extérieur des racines.
On rappelle que $S = x_1 + x_2 = \displaystyle \frac { - b} a$
On cherche le signe de $\displaystyle \frac S 2 - t$
… Si $\displaystyle \frac S 2 - t < 0$ , alors $x_1 < x_2 < t$
(car $S/2< t$ et $t$ à l’extérieur des racines donnent : $t$ est à « droite » de $x_2\,$ )
… Si $\displaystyle \frac S 2 - t > 0$ , alors $t < x_1 < x_2$
(car $S/2> t$ et $t$ à l’extérieur des racines donnent : $t$ est à « gauche » du réel $x_1\,$ ).
👍 : on aura intérêt à faire au brouillon un dessin de la droite réelle, des points d’abscisse $x_1\,$ , $x_2$ et $t$ (et $S/2$ ).

2. Quelques conseils et recommandations pour les inégalités

$\bullet$ Pensez à vérifier les affirmations à chaque étape !
$\ast$ Vous multipliez une inégalité par une expression : est-elle positive ou nulle ? ( ⚠️ méfiez-vous des expressions qui dépendent d’un paramètre ou d’une variable).
$\ast$ Si vous avez multiplié par un nombre négatif, avez-vous changé le sens de l’inégalité ?
$\quad \quad a \leq b$ et $c \geq 0$ $\Rightarrow a \, c \leq b \, c$ .
$\quad \quad a \leq b$ et $c < 0$ $\Rightarrow b \, c \leq a \, c$ .

$\ast$ Vous supprimez dans une inégalité le dénominateur, est-il strictement positif ?
$\quad$ si $b > 0$ , $\displaystyle\frac {a} {b} \leq \frac {a'} {b} \Leftrightarrow a \leq a '$ .

$\ast$ Vous multipliez deux inégalités entre-elles : aviez vous
$\quad \quad 0 \leq a \leq b$ et $0 \leq a' \leq b'$
pour pouvoir dire que $a\, a' \leq b \, b'$ ?

$\ast$ Vous passez à l’inverse : les nombres sont-ils strictement positifs ? Avez vous pensé à changer le sens de l’inégalité ?
$\quad \quad 0 < a \leq b \Rightarrow \displaystyle \frac 1 b \leq \frac 1 a$ .

$\ast$ Vous voulez conserver une inégalité stricte par multiplication par un réel, ce nombre est-il strictement positif ?
$\quad \quad a < b$ et $c > 0$ $\Rightarrow a\, c < b\, c$ .

$\ast$ Vous élevez une inégalité au carré : les deux nombres sont-ils positifs ?
$\quad \quad 0 \leq a \leq b \Rightarrow a^2 \leq b ^2$ .

$\bullet$ Démontrer une inégalité stricte demande en général plus de précautions que la démonstration d’une inégalité large. Inutile de vous compliquer la vie quand ce n’est pas indispensable, démontrer l’inégalité large si telle est la question !.

$\bullet$ Vous voulez majorer le réel positif $\displaystyle \frac a b$ .
Prenez le temps de vérifier que $0 \leq a$ puis cherchez $b' > 0$ tel que $b \geq b' > 0$ , alors $\displaystyle \frac a b \leq \frac {a} {b'}$ .
Un calcul de tête risque d’être faux et ne sera jamais justifié !

$\bullet$ Vous voulez prouver que $\quad \quad \forall \, x \in \, I , \, f(x) \geq 0$ .
⚠️ : Si vous partez de l’inégalité $f(x) \geq 0$ pour arriver par des implications ou sans faire apparaître le type de raisonnement à une inégalité vraie, vous n’aurez pas prouvé que $f(x) \geq 0$ .
Il est indispensable dans ce type de raisonnement de mettre en évidence un raisonnement correct par équivalen- ce pour arriver à une propriété vraie pour tout $x \in I$ .

$\bullet$ ⚠️ faute : ne faites pas de différence d’inégalités !
si vous avez $a \leq b$ et $c \leq d$ , vous pouvez conclure que $a - d \leq b - c$ et surtout pas $a - c \leq b - d$ !

$\bullet$ ⚠️ faute : pas de quotient d’inégalités
si vous avez $0 < a \leq b$ et $0 < c \leq d$ , vous pouvez conclure que $\displaystyle \frac a d \leq \frac b c$ et surtout pas $\displaystyle \frac a c \leq \frac b d$ !

$\bullet$ Ne croyez pas aux miracles : quand on demande de prouver qu’une inégalité $(I_1)$ implique une inégalité $(I_2)$ , il est rare qu’en faisant subir différentes transformations à $(I_1)$ on ait la chance de tomber sur $(I_2)$ .

Voici un exemple de ce qu’il ne faut pas faire :
Si l’hypothèse est $- 1 \leq x \leq 1$ et la conclusion $- 1 \leq 4 \, x^3 - 3 \, x \leq 1$ ,

$\bullet$ croire au miracle serait de commencer par écrire
$\quad \; - 4 \leq 4 \, x ^3 \leq 4$ et $- 3 \leq - 3\, x \leq 3$
puis par somme $-7 \leq 4 \, x^3 - 3 x \leq 7$ , vous êtes bien loin de l’inégalité à prouver.

$\bullet$ Ce qu’il faut faire : factoriser $\quad 1 - (4 \, x ^3 - 3 \, x)$ et $(4 \, x ^3 - 3 \, x) + 1$
pour démontrer que ces expressions sont positives ou nulles sur $[ - 1 \, , \, 1]$ .

On introduit $P$ et $Q$
$\ast$ $P(x) = 1 - (4 \, x ^3 - 3 \, x)$ , $P$ admet 1 pour racine, donc on peut écrire
$P(x) = 1 + 3 \, x - 4\, x^3$
$P(x) = (1 -x) (1 +a \, x + 4 \, x^2)$
(on compare les termes constants et les coefficients de plus haut degré pour n’avoir qu’un seul coefficient à déterminer.)
On obtient $a = 4$ en cherchant le coefficient de $x$ : $- 1 + a = 3$ .
$P(x) =(1 - x)(1 + 2 \, x) ^2$ est du signe de $1 - x$ .
Donc si $x \in [- 1 , \, 1], P(x) \geq 0$ .

$\ast$ Puis $Q(x) = (4 \, x ^3 - 3 \, x) + 1$ admet $- 1$ pour racine, donc on peut écrire
$Q(x) = 4 \, x ^3 - 3 \, x + 1$ $Q(x) = (x + 1)(4 \, x^2 + b \, x + 1)$
et on obtient $b = - 4$ donc
$Q(x) = (x + 1) (2 \, x - 1) ^2$ est du signe de $x + 1$ .
Donc si $x \in [- 1 , \, 1], Q(x) \geq 0$ .

On a donc prouvé que si $x \in [- 1 , \, 1]$ , $4 \, x ^3 - 3 \, x \in [- 1 , \, 1]$ .

3. Pour démontrer une inégalité du type $u(x) \leq v(x)$

👍 Il est conseillé de se ramener systématiquement (sauf en présence de racine carrée) à une inéquation de la forme $v(x) - u(x) \geq 0$ .

$\bullet$ $u$ et $v$ sont des fonctions polynômes, est-il possible de factoriser $u - v$ ? (chercher s’il y a des racines évidentes et ensuite chercher le signe des facteurs ainsi mis en évidence.)

$\bullet$ $u$ et $v$ sont des fractions rationnelles réduire $u - v$ au même dénominateur pour écrire $u(x) - v(x) = \displaystyle \frac {P(x)} {Q(x)}$ et étudier le signe de $P(x)$ et celui de $Q(x)$ .
Il est conseillé de présenter les résultats avec un tableau de signes.

$\bullet$ Pour démontrer que $\sqrt{u(x)} \leq v(x)$
On vérifie que $u(x)$ et $v(x)$ sont à valeurs positives ou nulles, on utilise ensuite l’équivalence :
$\quad \sqrt{u(x)} \leq v(x)$ $\Leftrightarrow u(x) \leq v^2(x)$ .

$\bullet$ Pour démontrer que $u(x) \leq \sqrt{v(x)}$
$\ast$ l’inégalité est évidente lorsque $u(x) < 0$ et $v(x) \geq 0$
$\ast$ dans le cas où $u(x) \geq 0$ et $v(x) \geq 0$
$u(x) \leq \sqrt{v(x)}$ $\Leftrightarrow u^2(x) \geq v(x)$ .

$\bullet$ Pour démontrer que $\vert u(x) \vert \leq v(x)$ ,
on peut :
$\ast$ prouver que $- v(x) \leq u(x) \leq v(x)$
$\ast$ étudier le signe de $u(x)$ pour éventuellement supprimer la valeur absolue
$\ast$ après avoir vérifié que $v(x) \geq 0$ , utiliser
$\quad \vert u(x) \vert \leq v(x)$ $\Leftrightarrow u^2(x) \leq v ^2(x)$ .

$\bullet$ Dans les autres cas, on étudie les variations de $w : x \mapsto u(x) - v(x)$ .
On donne le tableau de variations (ce qui est toujours plus explicite qu’un long discours).

$\bullet$ Pour démontrer que $u(x) < v(x)$ sur $I =\; ]a , \, b]$ ou $I =\; ]a , \,\, b[$ .
$\ast$ si vous voulez utiliser la valeur en $a$ , il suffit de pouvoir dire que $v - u$ est continue sur $J = [a , \, b[$ ou $[a ,\, b]$ , que $v - u$ est strictement croissante sur $I$ (c’est le cas si $(v - u)'(x) > 0$ sur $I$ . ) Dire ensuite que $u$ est strictement croissante sur $J$ (attention pas sur $I$ ) et que si $x \in J,$ $\quad \quad v (x) - u(x) > v(a) - u(a)$ ,
il suffit que $v(a) - u(a) \geq 0$ . pour obtenir l’inégalité stricte souhaitée.

Exemple prouver que pour tout $x > 0,$ $\quad \quad \quad \,\ln(1 + x) < x$ .

Correction :
On note $f : x \mapsto x - \ln(1 + x)$ .
$f$ est continue sur $[0 , \, + \infty[$ , dérivable sur $\mathbb{R }^{+ *}$ et $f'(x) = \displaystyle \frac x {1 + x} > 0$ si $x > 0$ .
$f$ est strictement croissante sur $\mathbb{R}^+$ , donc si $x > 0,\, f(x) > f(0)$ soit $f(x) > 0$ .

4. Utilisation de valeurs absolues

$\bullet$ Inégalité triangulaire :
$\ast$ si $x$ et $y$ sont des réels, $\quad \quad \vert x + y \vert \leq \vert x \vert + \vert y \vert$
$\ast$ et sa conséquence : $\quad \quad \vert \, \vert x \vert - \vert y \vert \, \vert \leq \vert x - y \vert$ .

$\ast$ sa généralisation à $n$ réels $(x _1 \, , \, x_2 \, , \, \cdots \, , \, x_n )$ ,
$\quad \quad \displaystyle \left \vert \sum _ {k = 1} ^n x_ k \right \vert \leq \sum _ {k = 1} ^{n} \vert x_ k \vert$ .

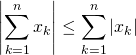$\bullet$ Une astuce de calcul classique :
si $x$ et $a$ sont réels
$\vert x \vert = \vert x + a + (- a) \vert \leq \vert x + a \vert + \vert a \vert$ .
et aussi
$\vert x \vert = \vert x - a + (a) \vert \leq \vert x - a \vert + \vert a \vert$ .

$\bullet$ Pour démontrer que $\vert f(x)\vert \leq \alpha$ , il suffit de prouver que $f(x) \leq \alpha$ et $- f(x) \leq \alpha$ .

$\bullet$ Connaître l’équivalence évidente :
$\quad \quad \vert y \vert \leq \alpha$ $\Leftrightarrow - \alpha \leq y \leq \alpha$

$\bullet$ ⚠️ aux risques d’erreurs
Si $a \leq b$ , vous ne pouvez pas conclure que $\vert a \vert \leq \vert b \vert$ .
Par exemple $- 2 \leq 1$ et $\vert - 2 \vert > \vert 1 \vert$ .

$\bullet$ 👍 : pour obtenir une majoration de $\vert f(x) \vert$ , commencer par écrire $\vert f(x)\vert$ avant de faire quelque majoration que ce soit sur $f(x)$ , il sera trop tard pour passer à la valeur absolue, sauf si les inégalités portent sur des nombres positifs !

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

5. Parties majorées, minorées, bornées

5.1. Définition
$\bullet$ Soit $A$ une partie non vide de $\mathbb{R}$ ,
$\ast$ $A$ est majorée s’il existe $M \in \mathbb{R}$ tel que $\forall \, a \in A,\, a \leq M$ .
⚠️ à l’ordre des quantificateurs !
$M$ est un majorant de $A$ et tout réel $M' \geq M$ est un majorant de $A$ .

$\ast$ $A$ est minorée s’il existe $m \in \mathbb{R}$ tel que $\forall \, a \in A,\, m \leq a$
⚠️ à l’ordre des quantificateurs !
$m$ est un minorant de $A$ et tout réel $m' \leq m$ est un minorant de $A$ .

$\bullet$ Soit $A$ une partie non vide
$\ast$ Si $A$ est une partie de de $\mathbb{R}$ , $A$ est bornée si elle est majorée et minorée.
👍 Il est plus simple de traduire $A$ bornée par : il existe $M \in \mathbb{R}^+$ tel que $\forall \, a \in A,\, \vert a \vert \leq M$ .

$\ast$ Si $A$ est une partie de $\mathbb{C}$ , $A$ est bornée s’il existe $M \in \mathbb{R}^+$ tel que $\forall \, a \in A,\, \vert a \vert \leq M$

5.2. Plus grand et plus petit élément
$\bullet$ Une partie non vide de $\mathbb{R}$ admet un plus grand élément $M$ lorsqu’il existe $M \in A$ tel que $\forall \, a \in A,\, a \leq M$ .
Alors $M$ est unique et noté $\quad \quad \quad \quad M = \max A$ .

$\bullet$ Une partie non vide de $\mathbb{R}$ admet un plus petit élément $m$ lorsqu’il existe $m \in A$ tel que $\forall \, a \in A,\, m \leq a$ .
Alors $m$ est unique et noté $m = \min A$ .

$\bullet$ Si $x$ et $y$ sont réels, on note
$\ast$ $\max(x , y)$ le plus grand élément de $\{x \, , \, y\}$
$\ast$ $\min (x , y)$ le plus petit élément de $\{x \, , \, y\}$ .
On peut vérifier que
$\ast$ $\max (x , \, y) = \displaystyle \frac 1 2 \left ( x + y + \vert x - y \vert \right )$
$\ast$ $\min (x , \, y) = \displaystyle \frac 1 2 \left ( x + y - \vert x - y \vert \right )$ .

$\bullet$ Cas particuliers.
$\ast$ Toute partie finie non vide de $\mathbb{R}$ admet un plus petit et un plus grand élément.
$\ast$ Toute partie non vide de $\mathbb{N}$ admet un plus petit élément
$\ast$ Toute partie finie non vide de $\mathbb{N}$ admet un plus grand élément.

5.3. Borne supérieure
$\bullet$ Si $A$ est une partie majorée non vide de $\mathbb{R}$ , l’ensemble des majorants de $A$ admet un plus petit élément qui est appelé borne supérieure de $A$ et noté $\sup A$ .

$\bullet$ Si $A$ est une partie majorée non vide de $\mathbb{R}$ , il y a équivalence entre :
$\ast$ $\alpha = \sup A$

$\ast$ $\forall \, a \in A ,\, a \leq \alpha$
et pour tout $\gamma < \alpha ,\, \gamma$ n’est pas un majorant de $A$ .

$\ast$ $\forall \, a \in A ,\, a \leq \alpha$
et pour tout $\gamma < \alpha$ , $\exists\, b \in A ,\, \gamma < b$

$\ast$ $\forall \, a \in A ,\, a \leq \alpha$
et il existe une suite $(a_n)_n$ de $A$ qui converge vers $\alpha$ .

Correction :

$\bullet$ Si $\alpha = \sup A$
$\ast$ $\forall \, a \in A ,\, a \leq \alpha$
$\ast$ $\forall \, n \in \mathbb{N}$ , $\displaystyle \alpha - \frac 1 {n + 1} < \alpha$ donc n’est pas un majorant de $A$ , il existe donc $a_n \in A$ tel que $\displaystyle \alpha - \frac 1 {n + 1} < a_n \leq \alpha$ .
Par encadrement, $\displaystyle \lim _{n \to +\infty} a_n = \alpha$ .

$\bullet$ On suppose que $\forall \, a \in A ,\, a \leq \alpha$ et qu’il existe une suite $(a_n)_n$ de $A$ qui converge vers $\alpha$
Soit $\gamma < \alpha$ et on traduit $\displaystyle \lim _{n \to +\infty} a_n = \alpha$ , en prenant $\varepsilon = (\alpha - \gamma) / 2$
il existe $N \in \mathbb{N}$ tel que si $n \geq N$ , $\quad \quad \vert a_n - \alpha \vert \leq \varepsilon$ $\Rightarrow \displaystyle - \frac {\alpha - \gamma} 2 \leq a_n - \alpha$
en particulier, $\displaystyle a_N \geq \frac {\alpha + \gamma} 2 > \gamma$ .
On a prouvé que $\gamma$ n’est pas un majorant de $A$ .

👍 seule l’implication :
Si $A$ est une partie majorée non vide de $\mathbb{R}$ ,
$\alpha = \sup A$ $\Rightarrow$ Il existe une suite $(a_n)_n$ de $A$ qui converge vers $\alpha$
est au programme.
C’est en fait l’implication la plus utile.

👍 Si l’ensemble $A$ admet une borne supérieure $M$ ,
$\ast$ si $M'$ est un réel tel que pour tout $a \in A$ , $a \leq M'$ , $M'$ est un majorant de $A$ , donc $M \leq M'$ .
$\ast$ en introduisant une suite bien choisie $(a_n)_n$ de $A$ , si cette suite converge vers $L$ , en écrivant que pour tout $n \in \mathbb{N}$ , $a_n \leq M$ et en passant à la limite, on obtient $L \leq M$ .

5.4. Borne inférieure
$\bullet$ Si $A$ est une partie minorée non vide de $\mathbb{R}$ , l’ensemble des minorants de $A$ admet un plus grand élément qui est appelé borne inférieure de $A$ et noté $\inf A$ .

$\bullet$ Si $A$ est une partie minorée non vide de $\mathbb{R}$ , il y a équivalence entre :
$\ast$ $\beta = \inf A$

$\ast$ $\forall \, a \in A ,\, \beta \leq a$
et pour tout $\gamma > \beta ,\, \gamma$ n’est pas un minorant de $A$ .

$\ast$ $\forall \, a \in A ,\, \beta \leq a$
et pour tout $\gamma > \beta$ , $\exists \, b \in A ,\, b < \gamma$

$\ast$ $\forall \, a \in A ,\, \beta \leq a$
et Il existe une suite $(a_n)_n$ de $A$ qui converge vers $\beta$

démonstration de la dernière équivalence

$\bullet$ Si $\beta = \inf A$
$\ast$ $\forall \, a \in A ,\, \beta \leq a$
$\ast$ $\forall \, n \in \mathbb{N}$ , $\displaystyle \beta + \frac 1 {n + 1} > \beta$ donc n’est pas un minorant de $A$ , il existe donc $a_n \in A$ tel que $\displaystyle \beta \leq a_n < \beta + \frac 1 {n + 1}$ .
Par encadrement, $\displaystyle \lim _{n \to +\infty} a_n = \beta$ .

$\bullet$ On suppose que $\forall \, a \in A ,\, \beta \leq a$ et qu’il existe une suite $(a_n)_n$ de $A$ qui converge vers $\beta$ .
Soit $\beta < \gamma$ . On traduit $\displaystyle \lim _{n \to +\infty} a_n = \beta$ , en prenant $\varepsilon = (\gamma - \beta) / 2$ , il existe $N \in \mathbb{N}$ tel que si $n \geq N$ , $\quad \quad \vert a_n - \beta \vert \leq \varepsilon$ $\Rightarrow \displaystyle a_n - \beta \leq \frac {\gamma - \beta} 2$
en particulier $\displaystyle a_N \leq \frac {\gamma + \beta} 2 < \gamma$ .
On a prouvé que $\gamma$ n’est pas un minorant de $A$ .

👍 seule l’implication :
Si $A$ est une partie minorée non vide de $\mathbb{R}$ ,
$\beta = \inf A$ $\Rightarrow$ Il existe une suite $(a_n)_n$ de $A$ qui converge vers $\alpha$
est au programme.
C’est en fait l’implication la plus utile.

👍 Si l’ensemble $A$ admet une borne inférieure $m$ ,
$\ast$ si $m'$ est un réel tel que pour tout $a \in A$ , $a \geq m'$ , $m'$ est un minorant de $A$ , donc $m' \leq m$ .
$\ast$ en introduisant une suite bien choisie $(a_n)_n$ de $A$ , si cette suite converge vers $L$ , en écrivant que pour tout $n \in \mathbb{N}$ , $a_n \geq m$ et en passant à la limite, on obtient $L \geq m$ .

$\bullet$ Si $A$ est une partie non vide de $\mathbb{R}$
$\alpha = \max A$ ssi $\alpha \in A$ et $\alpha = \sup A$ .

$\bullet$ Si $A$ est une partie non vide de $\mathbb{R}$
$\beta= \min A$ ssi $\beta \in A$ et $\beta = \inf A$ .

exemple : si $a , \, b$ sont réels et vérifient $a < b$ , $[a , b [$ est un intervalle borné, admettant une borne supérieure $a$ , mais pas de plus grand élément, et admet un plus petit élément égal à $b$ .

6. Utiliser la partie entière

$\bullet$ Si $x \in \mathbb{R}$ ,
$\ast$ $\lfloor x \rfloor$ est l’unique élément de $\mathbb{Z}$ tel que $\lfloor x \rfloor \leq x < \lfloor x \rfloor + 1$ .
$\ast$ C’est aussi l’unique élément de $\mathbb{Z}$ tel que $x - 1 < \lfloor x \rfloor \leq x$ .
$\ast$ C’est l’unique élément de $\mathbb{Z}$ tel que $x = \lfloor x \rfloor + \alpha$ où $\alpha \in [0 \, , \, 1[$ .

$\bullet$ Pour tout $n \in \mathbb{N}$ , $x_n = \lfloor x . 10 ^n \rfloor . 10 ^{-n}$ vérifie
$\ast$ $x_n \leq x < x_n + 10 ^{- n}$ .
On dit que $x_n$ est la valeur approchée par défaut de $x$ à $10 ^{-n}$ près et que $x_n + 10 ^{- n}$ est la valeur approchée par excès de $x$ à $10^{-n}$ près.
$\ast$ La suite $(x_n)_n$ est une suite de rationnels qui converge vers $x$ .

$\bullet$ La fonction $x \mapsto \lfloor x \rfloor$ est croissante sur $\mathbb{R }$ et vérifie
$\quad \forall \, x \in \mathbb{R},\, \lfloor x + 1 \rfloor = \lfloor x \rfloor + 1$ .

$\bullet$ Conséquence pour démontrer qu’une expression $f(x)$ dépendant de la partie entière est nulle, il suffit de trouver une période $P$ de $f$ et de démontrer que $f(x) = 0$ si $x \in [0 ,\, P[$ .

exemple
Calculer $\displaystyle \left \lfloor x + \frac 1 2 \right \rfloor- \left \lfloor x - \frac 1 2 \right \rfloor$ .

Correction

Soit $f(x) = \displaystyle \left \lfloor x + \frac 1 2 \right \rfloor- \left \lfloor x - \frac 1 2 \right \rfloor$ .
En utilisant $\forall\, y \in \mathbb {R}, \lfloor y + 1 \rfloor = \lfloor y \rfloor + 1$ ,
On obtient pour tout $x \in \mathbb{R}$ ,
$f(x + 1) = \displaystyle \left \lfloor x + \frac 1 2 \right \rfloor + 1 - \left \lfloor x - \frac 1 2 \right \rfloor - 1$
$f(x + 1) = f(x)$ .
$f$ est 1-périodique
$\ast$ Si $x \in [0 , 1/2[,\, x + 1/2 \in [1/2 , 1[$ et $x - 1/2 \in [-1/2 \, , \, 0[$ , $f(x) = 0 - (-1) = 1$
$\ast$ Si $x \in [1/2 , 1[, \, x + 1/2 \in [1 , 3/2[$ et $x - 1/2 \in [0 \, , \, 1/2[$ , $f(x) = 1 - 0 = 1$ .

$\forall\, x \in [0 , 1[,\, f(x) = 1$ .
Par 1-périodicité, le résultat est valable pour tout réel $x$ .

7. Intervalle de $\mathbb{R}$

$\bullet$ Pour démontrer que qu’une partie non vide $I$ de $\mathbb{R}$ est un intervalle de $\mathbb{R}$ , on prouve que si $(a , b) \in I^2$ avec $a \leq b$ $[a , b] \subset I$ c’est à dire que $\quad \forall\, t \in [0 , 1], t \, a + (1 - t) \ b \in I$ .

$\bullet$ Tout intervalle ouvert non vide de $\mathbb{R}$ contient un rationnel (et un décimal) et un irrationnel.
On dit que l’ensemble des décimaux, $\mathcal{Q}$ et $\mathcal{R} \setminus \mathcal{Q}$ sont denses dans $\mathcal{R}$ .

Poursuivez vos révisions avec les chapitres suivants du programme de mathématiques en Maths Sup :