Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les Nombres réels en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Inégalité de Cauchy-Schwarz
1. Sur la partie entière
2. Inégalités
3. Parties bornées
4. Inégalité de Cauchy-Schwarz
Ces exercices sur les nombres réels sont classiques et incontournables pour certains. Il est primordial de bien comprendre le cours et de savoir traiter ces exercices pour la suite de maths sup. Si vous souhaitez aller plus loin et exceller, n’hésitez pas à demander à Groupe Réussite de vous mettre en relation avec un professeur pour des cours particuliers de maths à domicile.
1. Sur la partie entière en MPSI, PCSI, MP2I et PTSI
Exercice 1
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : La propriété est fausse si ![]() , mais juste si
, mais juste si ![]() .
.
On suppose que ![]() . On note
. On note ![]() avec
avec ![]() et
et ![]()
donc ![]() avec
avec ![]() et
et ![]()
donc ![]() .
.
Exercice 2
![]()
Vrai ou Faux ?
Correction :
On rappelle quei ![]() .
.
![]() Autre méthode :
Autre méthode :
On utilise la périodicité ![]() de la fonction
de la fonction ![]() ainsi définie et et on étudie
ainsi définie et et on étudie ![]() sur
sur ![]() .
.
Soit si ![]() ,
, ![]()
![]()
Par le rappel,
![]()
![]() .
.
![]() est 1-périodique .
est 1-périodique .
![]() si
si ![]() , et
, et ![]()
![]() si
si ![]() , et
, et ![]()
si ![]() ,
, ![]() .
.
Par 1-périodicité, le résultat est valable pour tout réel ![]() .
.
Exercice 3
Si ![]() et
et ![]() , calculer
, calculer
![]()
Correction : Les entiers ![]() et
et ![]() sont de même parité (car leur somme
sont de même parité (car leur somme ![]() est paire).
est paire).
![]() Cas où
Cas où ![]() et
et ![]() sont pairs.
sont pairs.
On écrit ![]() et
et ![]() avec
avec ![]()
donc ![]()
et ![]() et
et ![]()
![]()
or par somme de ![]() et
et ![]() ,
, ![]()
donc ![]() .
.
![]() Cas où
Cas où ![]() et
et ![]() sont impairs.
sont impairs.
On écrit ![]() et
et ![]() avec
avec ![]()
donc ![]()
![]() et
et ![]()
![]()
or par somme de ![]() et
et ![]() ,
, ![]()
donc ![]() .
.
Dans les deux cas, ![]() .
.
Exercice 4
Pour tout ![]() ,
,
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
![]()
![]()
puis ![]()
donc ![]()
et ![]()
ce qui donne ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Inégalités des nombres réels en prepa maths sup
Exercice 1
Soit ![]() .
.
Montrer que 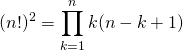
En déduire que ![]()
Correction :
![]()
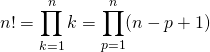
par changement d’indice :
![]() ssi
ssi ![]() .
.
![]() On introduit la fonction
On introduit la fonction ![]() définie sur
définie sur ![]()
![]() .
.
![]() est croissante sur
est croissante sur ![]() et décroissante sur
et décroissante sur ![]() , elle admet donc un maximum en
, elle admet donc un maximum en ![]()
et ![]() .
.
Le minimum de ![]() est égal à
est égal à ![]() car
car ![]() .
.
![]() En utilisant
En utilisant ![]()
et par produit de ces ![]() inégalités :
inégalités :
![]()
puis comme la fonction ![]() est croissante
est croissante
![]() .
.
Exercice 2
Peut on déterminer des réels ![]() tels que la fonction polynôme
tels que la fonction polynôme ![]() définie par
définie par
![]() soit négative ou nulle pour tout réel
soit négative ou nulle pour tout réel ![]() ? Est-ce Vrai ou Faux ?
? Est-ce Vrai ou Faux ?
Correction : ![]() Si
Si ![]() ,
, ![]() s’annule en changeant de signe en
s’annule en changeant de signe en ![]() , donc
, donc ![]() ne convient pas.
ne convient pas.
![]() Si
Si ![]() ,
,
![]()
![]()
![]()
![]()
![]() Si
Si ![]() ssi
ssi ![]() ,
, ![]() s’annule en changeant de signe, donc
s’annule en changeant de signe, donc ![]() ne convient pas.
ne convient pas.
![]() Si
Si ![]() ,
, ![]() est du signe du coefficient de
est du signe du coefficient de ![]() donc du signe de
donc du signe de ![]()
![]() ssi
ssi ![]() et
et ![]() si
si ![]() et
et ![]() (
(![]() est la racine double de
est la racine double de ![]() ).
).
Si ![]() ,
, ![]() ne s’annule pas et est du signe du coefficient
ne s’annule pas et est du signe du coefficient ![]() de
de ![]() .
.
Si ![]() .
.
Si ![]() .
.
En conclusion, ![]() pour tout
pour tout ![]() ssi
ssi ![]() .
.
Exercice 3
Suivant les valeurs du réel ![]() , étudier l’existence et le signe des racines réelles de l’équation
, étudier l’existence et le signe des racines réelles de l’équation
![]()
Correction : ![]() Si
Si ![]() , l’équation s’écrit
, l’équation s’écrit ![]() , elle admet une seule racine positive.
, elle admet une seule racine positive.
On suppose dans la suite que ![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]() lorsque
lorsque ![]() ou
ou ![]() , il n’y a pas de racine réelle.
, il n’y a pas de racine réelle.
![]()
![]() ssi
ssi ![]() ou
ou ![]()
Si ![]() , on obtient une racine double égale à 3 et si
, on obtient une racine double égale à 3 et si ![]() égale à
égale à ![]() .
.
![]() On suppose que
On suppose que ![]() soit
soit ![]() .
.
![]() La somme des racines est égale à
La somme des racines est égale à ![]() avec
avec ![]() .
.
![]() Le produit des racines est égal à
Le produit des racines est égal à ![]() .
.
On est amené à placer ![]() par rapport à
par rapport à ![]() et
et ![]() .
.
… Si ![]() ,
, ![]() ,
, ![]() et
et ![]() ,
, ![]() et
et ![]() . Les deux racines sont négatives.
. Les deux racines sont négatives.
… Si ![]() ,
, ![]() et
et ![]() , une racine est nulle, l’autre est strictement négative.
, une racine est nulle, l’autre est strictement négative.
… Si ![]() ,
, ![]() et
et ![]() . Les deux racines sont de signe opposé.
. Les deux racines sont de signe opposé.
… Si ![]() ,
, ![]() et
et ![]() . Les deux racines sont strictement positives.
. Les deux racines sont strictement positives.
3. Parties bornées en prepa MPSI, PTSI, PCSI et MP2I
Exercice 1
![]()
est une partie de ![]() n’admettant pas de plus grand élément mais telle que
n’admettant pas de plus grand élément mais telle que ![]() .
.
Correction :
![]() Si
Si ![]() avait un plus grand élément, il existerait
avait un plus grand élément, il existerait ![]() tel que
tel que ![]() , alors on devrait avoir en particulier
, alors on devrait avoir en particulier
![]()
donc ![]() ce qui implique
ce qui implique
![]() ce qui est absurde .
ce qui est absurde .
![]()
![]() est une partie de
est une partie de ![]() , non vide et majorée par 3. Elle admet une borne supérieure vérifiant
, non vide et majorée par 3. Elle admet une borne supérieure vérifiant
![]() .
.
Pour tout ![]() , on démontre que
, on démontre que ![]() n’est pas un majorant de
n’est pas un majorant de ![]() en cherchant
en cherchant ![]() tel que
tel que ![]()
c’est équivalent à ![]() .
.
Comme on compare des réels strictement positifs, c’est équivalent à
ssi ![]() .
.
La fonction ![]() étant strictement croissante, on a la CNS
étant strictement croissante, on a la CNS
ssi ![]()
ssi ![]()
en divisant par ![]()
ssi ![]()
Il suffit de choisir ![]() si c’est un entier positif et
si c’est un entier positif et ![]() = 0 sinon.
= 0 sinon.
On a prouvé que ![]() .
.
Exercice 2
Soient ![]() et
et ![]() deux parties non vides de
deux parties non vides de ![]() telles que
telles que ![]() .
.
Si ![]() est bornée,
est bornée, ![]() est bornée et
est bornée et
![]() et
et ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
![]() Si
Si ![]() est une partie bornée non vide de
est une partie bornée non vide de ![]() , on peut définir
, on peut définir ![]() et
et ![]() .
.
Pour tout ![]() ,
, ![]() , donc
, donc ![]()
![]() est bornée.
est bornée.
![]()
![]() est un minorant de
est un minorant de ![]() , il est donc inférieur ou égal à la borne inférieure de
, il est donc inférieur ou égal à la borne inférieure de ![]() , soit
, soit ![]() donc
donc ![]() .
.
![]()
![]() est un majorant de
est un majorant de ![]() , donc il est supérieur ou égal à la borne supérieure de
, donc il est supérieur ou égal à la borne supérieure de ![]() , donc
, donc ![]() , soit
, soit ![]() .
.
Exercice 3
Soient ![]() deux réels non tous les deux nuls. On note
deux réels non tous les deux nuls. On note ![]() .
.
![]() admet un minimum et un maximum. Vrai ou Faux ?
admet un minimum et un maximum. Vrai ou Faux ?
Correction :
On introduit le complexe non nul ![]() et sa forme exponentielle
et sa forme exponentielle
![]() avec
avec ![]() et
et ![]() .
.
Alors
![]()
![]()
donc ![]() .
.
![]() décrit
décrit ![]() si
si ![]() décrit
décrit ![]() .
.
![]() et
et ![]() existent et
existent et ![]() ,
, ![]() .
.
Exercice 4
Soient ![]() une partie borne non vide de
une partie borne non vide de ![]() . On note
. On note ![]() .
.
![]() .
.
Vrai ou Faux ?
Correction : ![]() est une partie bornée non vide de
est une partie bornée non vide de ![]() . On peut introduire
. On peut introduire ![]() et
et ![]() .
.
![]()
![]() , on écrit
, on écrit ![]() avec
avec ![]() , donc
, donc ![]() et alors
et alors ![]() .
.
![]() est une partie bornée non vide de
est une partie bornée non vide de ![]() admettant
admettant ![]() pour minorant et
pour minorant et ![]() pour majorant.
pour majorant.
donc ![]() et
et ![]() .
.
soit ![]() et
et ![]() .
.
![]() Puis en introduisant
Puis en introduisant ![]() ,
,
le raisonnement précédent donne en échangeant ![]() et
et ![]() ,
,
![]() et
et ![]() .
.
Soit ![]() et
et ![]() .
.
Par double inégalité,
![]() et
et ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Inégalité de Cauchy-Schwarz en prepa maths sup
Exercice 1
On suppose que ![]() et que
et que ![]() et
et ![]() sont deux familles de réels.
sont deux familles de réels.
Question 1
Soit ![]() et
et 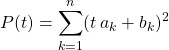
En développant ![]() , montrer l’inégalité de Cauchy-Schwarz :
, montrer l’inégalité de Cauchy-Schwarz :
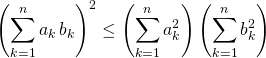
Correction :
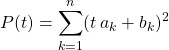
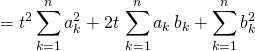
Expression que l’on écrit sous la forme
![]() .
.
On doit avoir pour tout réel ![]() ,
, ![]() .
.
![]() Si
Si ![]() , comme somme nulle de réels positifs ou nuls, on en déduit que
, comme somme nulle de réels positifs ou nuls, on en déduit que
![]() et l’inégalité est évidente, car elle s’écrit
et l’inégalité est évidente, car elle s’écrit ![]() .
.
![]() Si
Si ![]() ,
, ![]() est une fonction polynôme de degré 2 qui est positive ou nulle pour tout
est une fonction polynôme de degré 2 qui est positive ou nulle pour tout ![]() , donc
, donc
![]() soit
soit ![]() ce qui est l’inégalité demandée.
ce qui est l’inégalité demandée.
Question 2
L’inégalité précédente est une égalité si, et seulement si,
![]()
![]() ou
ou ![]() ,
, ![]() .
.
Correction :
On garde les notations de la démonstration de la question précédente.
![]() Si
Si ![]() , il y a égalité et cela correspond à la CNS :
, il y a égalité et cela correspond à la CNS : ![]() .
.
![]() Si
Si ![]() et s’il y a égalité, le discriminant de l’équation est nul, donc il existe
et s’il y a égalité, le discriminant de l’équation est nul, donc il existe ![]()
![]() soit comme somme nulle de réels positifs ou nuls,
soit comme somme nulle de réels positifs ou nuls, ![]() donc
donc ![]()
On démontre la réciproque.
On suppose qu’il existe ![]()
![]() .
.
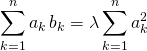
et 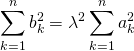 .
.
L’égalité est alors évidente.
Conclusion :
Il y a égalité ssi ![]() ou
ou ![]() .
.
Il est évident que l’on peut échanger les deux familles ![]() et
et ![]() dans la condition précédente.
dans la condition précédente.
Exercice 2 Deuxième démonstration
On suppose que ![]() et que
et que ![]() et
et ![]() sont deux familles de réels.
sont deux familles de réels.
Question 1
![]() ,
, ![]() .
.
Vrai ou Faux ?
Correction : ![]() .
.
Question 2
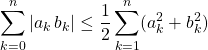 . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
On additionne les ![]() inégalités
inégalités
![]() .
.
Question 3
On suppose que les deux familles ![]() et
et ![]() contiennent au moins un élément non nul.
contiennent au moins un élément non nul.
Soit 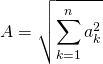 et
et 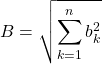 .
.
En utilisant les réels ![]() et
et ![]() si
si ![]() , démontrer l’inégalité de Cauchy-Schwarz :
, démontrer l’inégalité de Cauchy-Schwarz :
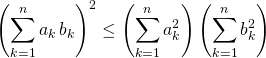
Correction :
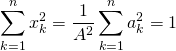
de même 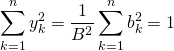
et 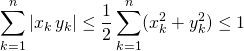
donne 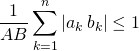
soit 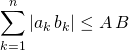 .
.
Par l’inégalité triangulaire,
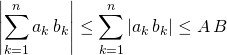
puis en élevant au carré,
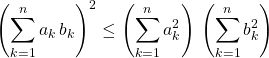
On a donc obtenu une autre démonstration de l’inégalité de Cauchy-Schwarz dans le cas de deux familles de réels non tous nuls.
Si l’une des familles est nulle, l’inégalité est évidente car elle s’écrit ![]() .
.
Maximisez vos résultats et votre moyenne en MPSI, PCSI et PTSI en révisant et en vous exerçant sur d’autres cours de Maths en Maths Sup :

