Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours en ligne Maths en Maths Sup

Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours : Primitives en MPSI, PCSI, MP2I et PTSI

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Maths Sup

Résumé de cours et méthodes – Primitives en Maths Sup

Plan :

Important : le seul but de ce chapitre est de savoir déterminer une primitive d’une fonction continue et d’introduire les théorèmes d’intégration par parties et de changement de variable.
La théorie de l’intégration sera étudiée au second semestre.

1. Primitives
2. Utilisation des intégrales
3. Théorème d’intégration par parties
4. Théorème de changement de variable
5. Les primitives à connaître
6. Les primitives à savoir calculer

1. Cours sur les primitives en MPSI, PCSI, PTSI, MP2I

On note $\mathbb{K} = \mathbb{C}$ ou $\mathbb{R}$ et $I$ un intervalle contenant au moins deux points de $\mathbb {R}$ .

Définition
$\bullet$   Si $f$ est une fonction définie sur $I$ à valeurs dans $\mathbb{K}$ , toute fonction $F$ dérivable sur $I$ et telle que $F' = f$ est appelée UNE primitive de $f$ sur $I$ .

Propriétés
$\bullet$   Si $f$ définie sur $I$ à valeurs dans $\mathbb{K}$ admet une primitive $F$ , $G$ est une primitive de $f$ sur $I$ ssi il existe $\lambda \in \mathbb{K}$ tel que $G = F + \lambda$ .
$\bullet$ Si $f$ définie sur $I$ à valeurs dans $\mathbb{K}$ admet une primitive $F$ et si $a \in I$ et $y_0 \in \mathbb{K}$ , il existe une et une seule primitive $F$ de $f$ sur $I$ telle que $F(a) = y_0\,$ .

$\bullet$ Soient $f$ et $g$ deux fonctions admettant respectivement $F$ et $G$ pour primitive sur $I$ ,
$\; \; \ast$ $F + G$ est une primitive de $f + g$ sur $I$ .
$\; \; \ast$ Si $\lambda \in \mathbb{K}$ , $\lambda \, F$ est une primitive de $\lambda\, f$ sur $I$ .
$\; \; \ast$ Soit $f = g + \textrm{i}\, h$ , où $g$ et $h$ sont définies sur $I$ à valeurs dans $\mathbb{R}$ .
$F$ est une primitive de $f$ sur $I$ ssi $\mathcal{R}e(F)$ (resp $\mathcal{I}m (F)$ ) est une primitive de $g$ (resp. $h$ ) sur $I$ .

$\bullet$ Si $f$ admet une primitive $F$ sur l’intervalle $I$ , si la fonction $u : J \to \mathbb{R}$ est dérivable sur $J$ et à valeurs dans $I$ , $F \circ u$ est une primitive de $u' \, f \circ u$ .

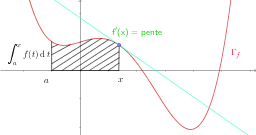
2. Utilisation des intégrales

$\bullet$ Si $f$ est continue sur l’intervalle $I$ à valeurs dans $\mathbb{C}$ , on note $f = g + \textrm{i} \, h$ où $g$ et $h$ sont continues à valeurs dans $\mathbb {R}$
si $a , b$ sont deux éléments de $I$ ,
$\int_a^b f(t) \, \textrm{d} \, t = \int_a^b g(t) \, \textrm{d} \, t + \textrm{i} \int_a^b h(t) \, \textrm{d} \, t$ .

$\bullet$ Si $f$ est continue sur l’intervalle $I$ à valeurs dans $\mathbb{C}$ , lorsque $a \in I$ , la fonction $F : x \mapsto \int_a ^x f(t) \, \textrm{d} \, t$ est dérivable sur $I$ de dérivée égale à $f$ .
C’est donc la primitive de $f$ sur $I$ s’annulant en $a$ .
Dans ce cas, $F$ est de classe $C ^1$ sur $I$ (dérivable à dérivée continue).

$\bullet$ Si $f$ est continue sur l’intervalle $I$ à valeurs dans $\mathbb{C}$ , pour toute primitive $F$ de $f$ sur $I$ , si $(a ,\, x) \in I^2$ ,
$\int_a ^x f(t) \, \textrm{d} \, t = F(x) - F(a) = \left [ F(t) \right] _ a ^x$

Conséquence : si l’on ne sait pas exprimer une primitive de la fonction continue $f$ sur l’intervalle $I$ , si l’on choisit $a \in I$ , la fonction $f$ définie par $\quad \quad F : x \mapsto \int_a ^x f(t) \, \textrm{d} \, t$
est une primitive de $f$ sur $I$ .
Ce sera le cas en particulier lorsque $f : t \mapsto \textrm {e}^ { - \alpha \, t ^2}$ où $\alpha \in \mathbb{R}^*$ .

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

3. Théorème d’intégration par parties

$\bullet$ Énoncé
Si les fonctions $u$ et $v$ sont de classe $C ^1$ sur l’intervalle $I$ à valeurs dans $\mathbb{K}$ et si $a$ et $b$ sont deux éléments distincts de $I$ ,
$\int_a ^b u'(t)\, v(t) \, \textrm{d} \, t =$ $\quad \quad \quad \left [ u(t) \, v(t) \right] _a ^b - \int_a ^b u(t)\ v'(t) \, \textrm{d} \, t$ .

$\bullet$ Rédaction : Pour être rigoureux il faut écrire (si nécessaire après recherche au brouillon) :
Soient $u : t \mapsto \, ??? \,$ et $v : t \mapsto \, ???\,$ deux fonctions de classe $C ^1$ sur $I$ .
Vous pouvez ensuite introduire les deux écritures suivantes qui vous permettent de mémoriser la démarche
$\left \{\ \begin{matrix} u'(t)&=&...\\v(t) &=&... \end{matrix} \right.$ et $\left \{\ \begin{matrix} u(t)&=&...\\v'(t) &=&... \end{matrix} \right.$

⚠️ Il faut faire attention à ne pas écrire « je pose $u'(t) = ...$ donc $u(t) = ...$ « .
Vous devez définir $u$ avant de définir $u'$ .

⚠️ N’oubliez pas d’écrire que $u$ et $v$ sont de classe $C ^1$ sur $I$ (à condition bien sûr qu’elles le soient !)

$\bullet$ Comment choisir $u$ et $v$ ?
$\ast$ Pour $f(t) = P(t) \ln (Q(t))$ où $P$ est une fonction polynôme (éventuelle- ment égale à 1), $u$ est une primitive de $P$ et $v : t \mapsto \ln( Q(t))$ .
Attention à l’intervalle, la fonction $t \mapsto \ln (t)$ n’est pas de classe $C^1$ sur $[0 , + \infty[$ .

$\ast$ Pour $f(t) = P(t)\, \textrm{Arctan} (Q(t))$ où $P$ est une fonction polynôme (éventuel- lement égale à 1), $u$ est une primitive de $P$ et $v : t \mapsto \textrm{Arctan} ( Q(t))$ .

👍 Une intégration par parties a pour but de simplifier l’intégrale à calculer et non de la compliquer !
En général, on choisit pour $v$ la partie de l’expression dont on voudrait se débarrasser sous réserve de ne pas compliquer le résultat final !

👍 Soit $f$ une fonction continue sur l’intervalle $I$ à valeurs dans $\mathbb{K}$ , pour déterminer une primitive de $f$ par une intégration par parties, on introduit $a \in I$ (que l’on peut choisir simple) et on calcule pour $x \in I$ , $\quad \quad \quad F(x) = \int_a^x f(t) \, \textrm{d} \, t$ .
Ayant obtenu à la fin $\quad \quad \quad F(x) = G(x) + \varphi(a)$
la fonction $G$ est une primitive de $f$ sur $I$ .

exemple 1 : fonction log
Primitives de $x \mapsto \ln(x)$ sur $\mathbb{R}^{+*}$ .

Correction : On note $F(x) = \int_{1} ^x \ln(t) \, \textrm{d} \, t$ .
Les fonctions $u : t \mapsto t$ et $v : t \mapsto \ln(t)$ sont de classe $C ^1$ sur $\mathbb{R}^{+*}$ .
$\left \{\ \begin{matrix} u'(t)&=&1\\v(t) &=&\ln(t) \end{matrix} \right.$ et $\left \{\ \begin{matrix} u(t)&=&t\\v'(t) &=&1/t \end{matrix} \right.$
$F(x) = \left [ t \ln(t) \right ] _1 ^x - \int_{1} ^x t / t \, \textrm{d} \, t$
$F(x) = \left [ t \ln(t) - t \right ] _1 ^x = x \, \ln(x) - x + 1$
L’ensemble des primitives de $\ln$ sur $\mathbb{R}^{+*}$ est l’ensemble des fonctions $\quad \quad x \mapsto x \, \ln(x) - x + C$ .

exemple 2 :
Si $P$ est une fonction polynôme de degré $n$ à coefficients dans $\mathbb{K}$ et $a \in \mathbb{K}^*$ , $x \mapsto P(x) \, \textrm{e} ^{a \, x}$ admet une primitive de la forme $x \mapsto Q(x) \, \textrm{e} ^{a \, x}$ où $Q$ est une fonction polynôme de degré $n$ .

Correction : On fixe $a \in \mathbb{K}^*$ .
Si $n \in \mathbb{N}$ , soit $H_n$ : Si $P$ est une fonction polynôme de degré $n$ à coefficients dans $\mathbb{K}$ , $x \mapsto P(x) \, \textrm{e} ^{a \, x}$ admet une primitive de la forme $x \mapsto Q(x) \, \textrm{e} ^{a \, x}$ où $Q$ est une fonction polynôme de degré $n$ .

$\ast$ $H_0$ est vraie car $x \mapsto \displaystyle \frac {\lambda} a \, \textrm{e} ^{a \, x}$ est une primitive de $x \mapsto \lambda \, \textrm{e} ^{a \, x}$ .

$\ast$ On suppose que $H_n$ est vraie.
Soit $P$ une fonction polynôme de degré $n + 1$ à coefficients dans $\mathbb{K}$ .
On note $F(x) = \int_0 ^x P(t) \, \textrm{e} ^{a \, t}\, \textrm{d} \, t$
Les fonctions $u : t \mapsto \displaystyle \frac 1 a \textrm{e} ^{a \, t}$ et $v = P$ sont de classe $C^1$ sur $\mathbb{R}$ .
$\left \{\ \begin{matrix} u'(t)&=&\textrm{e} ^{a \, t}&\\v(t) &=&P(t) \end{matrix} \right.$ , $\left \{\ \begin{matrix} u(t)&=&\textrm{e} ^{a \, t}/ a \\v'(t) &=&P\,'(t) \end{matrix} \right.$
Par intégration par parties :
$\displaystyle F(x) = \left [ \frac {P(t)} a \textrm{e} ^{a \, t} \right ] _0^x - \frac 1 a \int_0 ^x P\,'(t) \,\textrm{e} ^{a \, t} \textrm{d} \, t$

Comme $P\,'$ est une fonction polynôme de degré $n$ , par $H_n\,$ , il existe $Q$ fonction polynôme de degré $n$ telle que $t \mapsto Q(t) \, \textrm{e} ^{a \, t}$ est une primitive de $t \mapsto P\,'(t) \, \textrm{e} ^{a \, t}$
alors $F(x) = \displaystyle \left [ \frac 1 a \left ( P(t) - Q(t) \right ) \textrm{e} ^{a \, t} \right ] _ 0 ^x$

Donc $x \mapsto \displaystyle \frac 1 a \left ( P(x) - Q(x) \right ) \textrm{e} ^{a \, x}$ est une primitive de $f$ et $x \mapsto \displaystyle \frac 1 a \left ( P(x) - Q(x) \right )$ est une fonction polynôme de degré $n + 1$ (différence d’une fonction polynôme de degré $n + 1$ et d’une fonction polynôme de degré $n$ ).
La propriété est démontrée par récurrence.

👍 il sera plus simple d’écrire $F(x) = Q(x) \, \textrm{e} ^{a \, x}$ avec $P$ et $Q$ de même degré, de calculer $F'$ et d’écrire $F' = f$ pour déterminer $F$ .

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

Avis Google France ★★★★★ 4,8 sur 5

4. Théorème de changement de variable

$\bullet$ Enoncé : Si $\varphi$ est une fonction réelle de classe $C ^1$ sur l’intervalle $I$ et si $f$ est continue sur $\varphi(I)$ , pour tous $a$ et $b$ de $I$ ,
$\quad \int_{\varphi(a)} ^{\varphi(b)} f(t) \, \textrm{d} t = \int_ a ^b f (\varphi(u)) \, \varphi'(u) \, \textrm{d} \, u$

$\bullet$ Une première façon d’appliquer le théorème de changement de variable est de reconnaître dans l’intégrale à calculer une expression de la forme $\int_ a ^b f (\varphi(u)) \, \varphi'(u) \, \textrm{d} \, u$ .
On obtient alors une intégrale égale à $\int_{\varphi(a)} ^{\varphi(b)} f(t) \, \textrm{d} t$ .

Méthode pratique
Soit à calculer $\int_A ^B f(t) \, \textrm{d} \, t$ .
$t$ étant l’ancienne variable, chercher à écrire $t = \varphi (u)$ où $\varphi$ est de classe $C^1$ sur un intervalle $J$ à valeurs dans $I$ .
$\ast$ vérifier que l’on peut écrire $A = \varphi(a)$ et $B = \varphi(b)$ (ce sera le cas si $\varphi$ est une bijection de $J$ sur $I$ ).
$\ast$ remplacer $t$ par $\varphi(u)$ dans l’expression $f(t)$
$\ast$ remplacer $\textrm{d} \, t$ par $\varphi'(u) \, \textrm{d} \, u$ .

⚠️ lorsque l’énoncé donne le changement de variable sous la forme $u = \Psi(t)$ , il faut vérifier que la fonction $\Psi$ est bijective ce qui permet de se ramener à une écriture de la forme $t = \varphi(u)$ et d’utiliser la méthode indiquée ci-dessus sous réserve que $\varphi$ soit de classe $C^1$ .

⚠️ Lorsque l’on écrit $t = \varphi(u)$ , cela suppose que $u$ est défini de façon unique.
$\ast$ si l’on pose $t = u ^2$ , il faut ajouter $u \geq 0$ , ou dire que l’on utilise $\Psi : t \mapsto \sqrt{t}$ .
$\ast$ si l’on pose $t = \sin(u)$ , on impose $\vert u \vert \leq \pi /2$ , ou dire que l’on utilise $\Psi : t \mapsto \textrm{Arcsin} (t)$ .
$\ast$ si l’on pose $t = \cos(u)$ , on impose $u \in [0 , \, \, \pi]$ , ou dire que l’on utilise $\Psi : t \mapsto \textrm{Arccos} (t)$ .
$\ast$ si l’on pose $t = \tan(u)$ , on impose $- \pi/2 < u < \pi/2$ , ou dire que l’on utilise $\Psi : t \mapsto \textrm{Arctan}(t)$ .
$\ast$ si l’on pose $t = \tan(u/2)$ , on impose $- \pi < u < \pi$ , ou dire que l’on utilise $\Psi : t \mapsto 2 \, \textrm{Arctan}(t)$ .

$\bullet$ En pratique, on doit vous donner le changement de variable (il est possible qu’on ne le fasse pas lorsqu’il est de la forme $\varphi : u\mapsto \alpha\, u + \beta$ ).
Mais vous penserez peut-être tout seul aux changements de variables suivants ?
$\ast$ $\int_{a} ^{b} f(t^2 ) \, \textrm{d} t$ , on pose $\varphi (u) = \sqrt{u}$
ce qui donne $t^2 = u$
$\ast$ $\int_{a} ^{b} f(\textrm{e} ^{ t } ) \, \textrm{d} t$ , on pose $\varphi (u) = \ln(u)$
ce qui donne $\textrm{e} ^t = u$
$\ast$ $\int_{a} ^{b} f\left (\sqrt{\alpha \, t + \beta } , t \right ) \, \textrm{d} t$
pour avoir $u = \sqrt{\alpha \, t + \beta }$ , on pose $\varphi : u \mapsto \displaystyle \frac {u ^2 - \beta } {\alpha}$ .

👍 Soit $f$ une fonction continue sur l’intervalle $I$ à valeurs dans $\mathbb{K}$ , pour déterminer une primitive de $f$ par changement de variable, on introduit $a \in I$ (que l’on peut choisir simple) et on calcule pour $x \in I$ , $\quad \quad \quad F(x) = \int_a^x f(t) \, \textrm{d} \, t$ .
Lorsque le calcul se fait par changement de variable de la forme $t = \varphi(u)$ , on impose que $\varphi$ définisse une bijection pour pouvoir écrire :
$\displaystyle F(x) = \int_{\varphi(\varphi ^{- 1}(a))} ^{\varphi(\varphi ^{- 1}(x))} f(t) \, \textrm{d} \,t$ $F(x) \displaystyle = \int_ {\varphi ^{- 1}(a)} ^{\varphi ^{- 1}(x)} f (\varphi(u)) \, \varphi'(u) \, \textrm{d} \, u$ .
Ayant obtenu à la fin $\quad \quad \quad F(x) = G(x) + \varphi(a)$ ,
la fonction $G$ est une primitive de $f$ sur $I$ .

👍 On peut aussi effectuer le changement de variable en raisonnant ainsi ce qui rend la résolution plus simple :
$\ast$ on remplace $t$ par $\varphi(u)$
$\ast$ on remplace $\textrm{d} \, t$ par $\varphi'(u) \, \textrm{d} \, u$
$\ast$ on change les bornes en se posant les questions suivantes :
… Quelle est la valeur de $u$ lorsque $t = a$ (c’est $u = \varphi^{- 1} (a)$ ) ?
… Quelle est la valeur de $u$ lorsque $t = x$ (c’est $\varphi ^{ - 1} (x)$ ) ?

exemple 1
Trouver une primitive de $\quad \quad \quad t \mapsto \displaystyle \frac 1 {2 + \sqrt{t + 1}}$ .

Correction : $\bullet$ $D : t \mapsto 2 + \sqrt{t + 1}$ est définie sur $[- 1 \,, \, + \infty[$ est strictement croissante et vérifie $D(- 1) = 2$ donc $D(t) > 0$ .
La fonction $f$ est continue sur $[ - 1\,, \, \infty[$ .

$\bullet$ On note si $x \geq - 1$ ,
$\quad \quad F(x) = \displaystyle \int_0 ^x \frac 1 { 2 + \sqrt{t + 1}} \, \textrm{d} \, t$ .
La fonction $\psi : t \mapsto \sqrt{t + 1}$ est de classe $C ^1$ sur $]- 1 \, , \, +\infty[$ , sa fonction réciproque est $\varphi : u \mapsto u ^2 - 1$ de classe $C^1$ sur $[-1, \, +\infty[$ .

$\ast$ On pose $\varphi : u \mapsto u ^2 - 1$ , on obtient $t = u ^2 - 1 \Leftrightarrow u = \sqrt{ t +1}$ .
$\ast$ On remplace $\textrm{d} \, t$ par $\varphi'(u) \, \textrm{d} \, u$ soit par $\displaystyle 2 \, u \, \textrm{d}\,u$
$\ast$ Changement des bornes.
Si $t = 0$ , $u = 1$
si $t = x$ , $u = \sqrt{x + 1}$ .

Le théorème de changement de variable donne : $F(x) = \displaystyle \int_{0} ^{\sqrt{x + 1}} \frac 1 {2 + u } \, \, ( 2 \, u ) \, \textrm{d} u$
Puis en utilisant $\quad \quad \displaystyle \frac {2 \, u} {2 + u } = \frac {2 \, u + 4 } {2 + u }- \frac {4} {2 + u }$
$F(x) = \displaystyle \left [\, 2 \, u - 4\, \ln \vert 2 + u \vert \,\right ] _0 ^{\sqrt{x +1}}$

👍 Une primitive de $f$ est $x \displaystyle \mapsto 2 \sqrt{x +1} - 4 \ln \left ( 2 + \sqrt{x + 1} \right ) + C$ .

exemple 2
Primitives de $x \mapsto \displaystyle \frac 1 {\sin(x)}$ sur $]0,\,\pi [$ .

Correction : $\displaystyle f(x) = \frac 1 {\sin(x)} = \frac {\sin(x)} {\sin^2(x)} = \frac {\sin(x)} {1 - \cos^2(x)}$
On cherche une primitive sur $]0 , \, \pi[$ .
$F(x) = \displaystyle \int_{\pi/2} ^x \ \frac {\sin(u)} {1 - \cos^2(u)} \, \textrm{d} \, u$ .

On remarque que si l’on pose $\varphi : u \mapsto \cos(u)$ , on a écrit $F(x) = \displaystyle \int_{\pi/2} ^x \frac {- 1} {1 - \varphi^2 (u) } \varphi '(u) \, \textrm{d} \, u$ .
le théorème de changement de variable donne
$F(x) = \displaystyle \int_{\varphi(\pi/2)} ^{\varphi(x)} \frac {- 1} {1 - t^2 } \, \textrm{d} \, t$
$= \displaystyle \int_{0} ^{\cos(x)} \left ( \frac {- 1} {2 (1 - t) } + \frac {- 1} {2 (1 + t) } \right ) \, \textrm{d} \, t$
$F(x) = \displaystyle \left [ \frac 1 2 \ln \left ( \frac {1 - t } {1 + t}\right ) \right]_{0} ^{\cos(x)}$

Une primitive est donc $\quad \quad x \displaystyle \mapsto \frac 1 2 \ln \frac {1 - \cos(x) } {1 + \cos(x)}$
que l’on peut aussi écrire $x \mapsto \displaystyle \ln \left \vert \tan \frac x 2 \right \vert$

On en déduit qu’une primitive de $x \mapsto \displaystyle \frac 1 {\cos(x)}$ sur $]-\pi/2 \, , \, \pi/2 [$ est
$\quad \quad \quad x \mapsto \displaystyle \ln \left \vert \tan \left ( \frac x 2 + \frac {\pi} 4 \right ) \right \vert$ .
On a utilisé $\displaystyle \cos(x) = \sin \left ( x + \frac {\pi} 2 \right )$ .

exemple 3
Primitives de $x \mapsto \displaystyle \frac {1} {1 + \sqrt{1 - x^2}}$ .

Correction : On se place sur $] - 1 ,\, 1 [$ .
Soit si $x \in\; ] - 1 ,\, 1 [$ ,
$\quad \quad F(x) = \displaystyle \int_0^x \frac 1 {1 + \sqrt{1 - t^2}} \textrm{d} \, t$ .

On introduit $\varphi : u \mapsto \sin(u)$ définie sur $] - \pi/2 , \pi/2[$
alors $t = \varphi(u) = \sin (u)$
$\sqrt{1 - t ^2} = \sqrt{1 - \sin^2(u)} = \vert \cos (u) \vert$ $\sqrt{1 - t ^2} = \cos(u)$ car $\vert u \vert < \pi/2$ .

$\ast$ si $t = 0, \, u = 0$
$\ast$ si $t = x$ , $u = \textrm{Arcsin}(x)$ .

$F(x) = \displaystyle \int_0^x \frac 1 {1 + \sqrt{1 - t^2}} \textrm{d} \, t$
$F(x) = \displaystyle \int_{0} ^{\textrm{Arcsin}(x)}\frac 1 {1 + \cos (u)} \cos{(u)} \, \textrm{d} \, u$
$\displaystyle g(u) = \frac {\cos(u) } {1 + \cos(u)} = 1 - \frac 1 {1 + \cos (u)}$
$\displaystyle g(u) = 1 - \frac 1 {2 \, \cos^2(u/2)}$
$F(x) = \displaystyle \left [ u - \tan \left ( \frac u 2 \right ) \right ] _ 0^{\textrm{Arcsin}(x)}$

Primitives $x \displaystyle \mapsto \textrm{Arcsin}(x) - \tan \left ( \frac {\textrm{Arcsin}(x)} 2 \right ) + C$

On peut simplifier cette relation.
$\displaystyle \tan \frac t 2 = \frac {\sin(t/2)} {\cos(t/2)} = \frac {2 \, \sin(t/2) \, \cos(t /2) } {2 \, \cos^2(t/2)}$
$\displaystyle \tan \frac t 2 = \frac {\sin(t)} {1 + \cos(t)}$
Dans le cas où $t = \textrm{Arcsin}(x)$ , $\sin(t) = x$ et $\cos(t) = \sqrt{1 - x^2}$ ,
donc les primitives s’écrivent
$\quad \quad x \displaystyle \mapsto \textrm{Arcsin}(x) - \frac {x} {\sqrt{1 - x^2}} + C$ .

5. Les primitives à connaître

$\bullet$ sur $\mathbb{R}$ :
$\; \; \ast$ $x \mapsto \textrm{Arctan}(x)$ est une primitive de $x \mapsto \displaystyle \frac 1{1 + x^2}$
$\; \;\ast$ $\displaystyle x \mapsto \frac 1 {n + 1} x ^{n + 1}$ est une primitive de $x \mapsto x ^n$ où $n \in \mathbb{N}$
$\; \; \ast$ $x \mapsto \textrm{e} ^x$ est une primitive de $x \mapsto \textrm{e} ^x$
$\; \; \ast$ soit $(a , b) \in \mathbb{R} \times \mathbb{R}^*$ ,
$x \mapsto \displaystyle \frac 1 {a +\textrm{i} \, b} \textrm{e} ^{(a + \textrm{i}\, b) x }$ est une primitive de $x \mapsto \displaystyle \textrm{e} ^{(a + \textrm{i}\, b)x }$
$\; \; \ast$ $x \mapsto \cos(x)$ est une primitive de $x \mapsto \sin(x)$
$\; \; \ast$ $x \mapsto -\sin(x)$ est une primitive de $x \mapsto \cos(x)$
$\; \; \ast$ $x \mapsto \textrm{ch}(x)$ est une primitive de $x \mapsto \textrm{sh}(x)$
$\; \; \ast$ $x \mapsto \textrm{sh}(x)$ est une primitive de $x \mapsto \textrm{ch}(x)$
$\; \; \ast$ $x \mapsto \textrm{th}(x)$ est une primitive de $x \mapsto \displaystyle \frac 1 {\textrm{ch}^2(x)}$ .

$\bullet$ sur $\mathbb{R}^{+*}$ ou sur $\mathbb{R}^{- *}$ :
$\; \; \ast$ si $n \in \mathbb{Z} \setminus \mathbb{N}$ et $n \neq - 1$ ,
$x \mapsto \displaystyle \frac 1 {n + 1} x ^{n + 1}$ est une primitive de $x \mapsto x ^n$
$\; \; \ast$ $x \mapsto \ln \vert x \vert$ est une primitive de $x \mapsto \displaystyle \frac 1 x$ .

$\bullet$ sur $\mathbb{R}^{+*}$ :
$\; \; \ast$ si $\alpha \in \mathbb{R} \setminus \mathbb{Z}$ , $x \mapsto \displaystyle \frac 1 {\alpha + 1} x ^{\alpha + 1}$ est une primitive de $x \mapsto x ^{\alpha}$ .
$\; \; \ast$ $x \mapsto x \, \ln(x) - x$ est une primitive de $x \mapsto \ln(x)$ .

$\bullet$ sur $] - 1 \, , \, 1[$ , $x \mapsto \textrm{Arcsin}(x)$ est une primitive de $\displaystyle x \mapsto \frac 1 {\sqrt{1 - x^2}}$ .

$\bullet$ sur tout intervalle de la forme $]- \pi/2 + k \, \pi , \pi/2 + k \, \pi[$ où $k \in \mathbb{Z}$ :
$x \mapsto \tan(x)$ est une primitive de $x \mapsto 1 + \tan^2(x)= \displaystyle \frac 1 {\cos^2(x)}$ .

6. Les primitives à savoir calculer

$\bullet$ Si $(a , b) \in \mathbb{R} \times \mathbb{R}^*$ , pour trouver une primitive de $g : x \mapsto \cos(b \, x) \, \textrm{e} ^{a \, x}$ ou de $h : x \mapsto \sin(b \, x) \, \textrm{e} ^{a \, x}$ , on introduit
$f : x \mapsto \textrm{e} ^{(a + \textrm{i} \, b)x }$ dont une primitive est : $\quad \quad \quad F : x \mapsto \displaystyle \frac 1 {a +\textrm{i} \, b} \textrm{e} ^{(a + \textrm{i}\, b) x }$ .
Une primitive $G$ de $g$ (resp. $H$ de $h$ ) est $G = \mathcal{R}e(F)$ (resp $H = \mathcal{I}m(F)$ ).
Les calculs donnent
$G : x \mapsto \displaystyle \frac {a\, cos(b\,x) + b \, \sin(b\, x)} {a^2 + b^2} \, \textrm{e} ^{a\, x}$
$H : x \mapsto \displaystyle \frac {a\, \sin(b\,x) - b \, \cos(b\, x)} {a^2 + b^2} \, \textrm{e} ^{a\, x}$

$\bullet$ Pour trouver une primitive de $\quad \quad x \displaystyle \mapsto \frac 1 {a \, x ^2 + b \, x + c}$
où $(a , b , c) \in \mathbb{R}^* \times \mathbb{R} ^2$ , on note $P(x) = a \, x ^2 + b \, x + c$ et on distingue les cas :
$\ast$ $P$ a une racine double $r$ , on écrit $P(x) = a(x - r) ^2$ .
Une primitive de $x \mapsto \displaystyle \frac 1 {a(x - r) ^2}$ est $x \displaystyle \mapsto \frac {- 1} {a ( x- r)}$ sur tout intervalle ne contenant pas $r$ .

$\ast$ $P$ a deux racines réelles distinctes $r _1 < r_2$ , on écrit $\quad \quad P(x) = a(x - r_1)(x - r_ 2)$
On cherche $\lambda$ et $\mu$ dans $\mathbb{K}$ tels que $\quad \quad \displaystyle \frac 1 {P(x)} = \frac {\lambda } { x - r _ 1} + \frac {\mu} {x - r _ 2}$
et $\displaystyle \frac 1 P$ admet pour primitive $x \mapsto \displaystyle \lambda \ln \vert x - r _ 1 \vert + \mu \ln \vert x - r_2 \vert$ sur tout intervalle ne contenant ni $r_1$ ni $r_2\,$ .

$\ast$ $P$ n’a pas de racine réelle.
On écrit 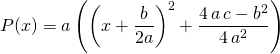$P(x) = \displaystyle a \left ( \left (x + \frac {b} {2 a} \right ) ^2 + \frac {4\, a \, c - b ^2} {4 \, a ^2} \right)$
soit une expression de la forme $P(x) = a\left ( (x + p)^2 + q^2 \right )$ $P(x) = \displaystyle a \, q^2 \left ( \left ( \frac {x + p} q \right )^2 + 1 \right )$
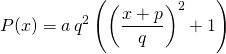
et $\displaystyle x \mapsto \frac 1 {a \, q} \textrm{Arctan} \left (\frac {x + p} q \right )$ est une primitive de $\displaystyle \frac 1 P$ .

Bénéficiez de nombreux cours en ligne gratuits et de cours de maths à domicile au programme de Maths Sup, pour prendre de l’avance et améliorer vos résultats en prépa :

Cours : Primitives en MPSI, PCSI, MP2I et PTSI

Résumé de cours et méthodes – Primitives en Maths Sup

Plan :

1. Cours sur les primitives en MPSI, PCSI, PTSI, MP2I

2. Utilisation des intégrales

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

3. Théorème d’intégration par parties

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

4. Théorème de changement de variable

5. Les primitives à connaître

6. Les primitives à savoir calculer

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Cours : Primitives en MPSI, PCSI, MP2I et PTSI

Résumé de cours et méthodes – Primitives en Maths Sup

Plan :

1. Cours sur les primitives en MPSI, PCSI, PTSI, MP2I

2. Utilisation des intégrales

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension clés de la réussite

Cours de maths en ligne ou à domicile

3. Théorème d’intégration par parties

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

4. Théorème de changement de variable

5. Les primitives à connaître

6. Les primitives à savoir calculer

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

La pratique et la compréhension
clés de la réussite