Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Systèmes en Maths Sup en MPSI, MP2I, PTSI, PCSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Systèmes en Maths Sup
Plan :
1. Introduction des notations
2. Opérations élémentaires
3. Méthode du pivot de Gauss
4. Interprétation géométrique
1. Introduction des notations
On note ![]() ou
ou ![]() .
.
On appelle système de ![]() équations à
équations à ![]() inconnues à coefficients dans
inconnues à coefficients dans ![]() tout ensemble
tout ensemble ![]() d’équations de la forme
d’équations de la forme
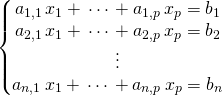
où les coefficients ![]() et
et ![]() sont dans
sont dans ![]() .
.
On dit que ![]() sont les seconds membres du système.
sont les seconds membres du système.
Un ![]() -uplet
-uplet ![]() est une solution de
est une solution de![]() si elle vérifie les
si elle vérifie les ![]() équations du système ;
équations du système ;
Résoudre![]() , c’est décrire l’ensemble
, c’est décrire l’ensemble ![]() des solutions de
des solutions de ![]() .
.
Le système ![]() est compatible s’il admet au moins une solution ; sinon,
est compatible s’il admet au moins une solution ; sinon, ![]() est dit incompatible.
est dit incompatible.
Le système ![]()
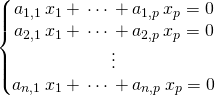
est appelé système homogène associé au système ![]() .
.
Il admet au moins la solution triviale
(![]() pour tout
pour tout ![]() ).
).
On note ![]() :
: ![]() la
la ![]() -ème équation du système.
-ème équation du système.
Le tableau ![]() à
à ![]() lignes et
lignes et ![]() colonnes
colonnes
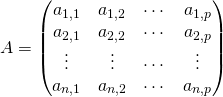
est la matrice associée au système ![]() .
.
Sous réserve d’avoir défini les opérations sur les matrices, en notant ![]() et
et ![]() , les matrices colonnes à
, les matrices colonnes à ![]() et
et ![]() lignes respectivement, le système
lignes respectivement, le système ![]() se traduit par
se traduit par ![]() et le système homogène associé s’écrit
et le système homogène associé s’écrit ![]() .
.
2. Opérations élémentaires
Si ![]() et
et ![]() , on note :
, on note :
![]()
![]() l’échange des lignes
l’échange des lignes ![]() et
et ![]() .
.
![]()
![]() la multiplication de la ligne
la multiplication de la ligne ![]() par
par ![]()
![]()
![]() l’ajout à la ligne
l’ajout à la ligne ![]() de
de ![]() fois la ligne
fois la ligne ![]() .
.
Toutes ces opérations donnent un système équivalent au système initial ![]() c’est-à-dire ayant les mêmes solutions que
c’est-à-dire ayant les mêmes solutions que ![]() .
.
Si ![]() et
et ![]() ,
,
![]()
donne un système équivalent au système initial. car c’est une composée de deux opérations élémentaires.
3. Méthode du pivot de Gauss
3.1. Transformation du système
![]() Traitement de la première colonne
Traitement de la première colonne
![]() On suppose qu’il existe
On suppose qu’il existe ![]() tel que
tel que ![]() (si ce n’est pas le cas, l’inconnue
(si ce n’est pas le cas, l’inconnue ![]() est absente).
est absente).
Quitte à utiliser ![]() , on peut supposer que
, on peut supposer que ![]() .
.
On dit que ![]() est le premier pivot.
est le premier pivot.
![]() Pour tout
Pour tout ![]() , on utilise
, on utilise
![]()
ce qui permet d’annuler les coefficients de ![]() dans les lignes
dans les lignes ![]() à
à ![]() .
.
La matrice ![]() associée à ce système équivalent
associée à ce système équivalent ![]() est
est
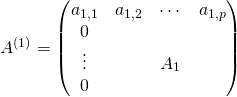
où ![]() a
a ![]() lignes et
lignes et ![]() colonnes.
colonnes.
Si ![]() , la transformation du système est terminée.
, la transformation du système est terminée.
![]() Recherche du pivot suivant lorsque
Recherche du pivot suivant lorsque ![]() .
.
On numérote les colonnes de ![]() de
de ![]() à
à ![]() et les lignes de
et les lignes de ![]() à
à ![]() .
.
Si ![]() est le numéro de la première colonne de
est le numéro de la première colonne de ![]() non nulle et si
non nulle et si ![]() , on échange si nécessaire les lignes
, on échange si nécessaire les lignes ![]() et
et ![]() du système
du système ![]() de sorte que
de sorte que ![]() .
.
On effectue pour tout ![]() ,
,
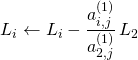
de façon à annuler les coefficients de ![]() dans les lignes
dans les lignes ![]() à
à ![]() .
.
On obtient un système équivalent ![]() admettant comme matrice associée :
admettant comme matrice associée :
![]()
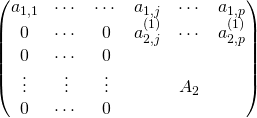
![]() On recommence avec
On recommence avec ![]() si
si ![]() .
.
3.2. Discussion du système
On obtient l’existence d’un entier ![]() et des pivots
et des pivots
![]() ,
, ![]() ,
, ![]() ,
, ![]() tels que le système soit équivalent au système :
tels que le système soit équivalent au système :
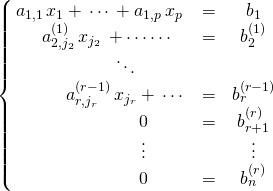
On dit que l’entier ![]() est le rang du système
est le rang du système ![]() .
.
Les ![]() dernières équations étant absentes lorsque
dernières équations étant absentes lorsque ![]() .
.
![]() Si
Si ![]() et si l’un des coefficients
et si l’un des coefficients ![]() est non nul, le système est impossible.
est non nul, le système est impossible.
![]() Si
Si ![]() et si
et si ![]() , le système est équivalent au système formé par les
, le système est équivalent au système formé par les ![]() premières équations. Le système est dit compatible.
premières équations. Le système est dit compatible.
![]() Si
Si ![]() ,
, ![]() , le système admet une unique solution : on résout l’équation
, le système admet une unique solution : on résout l’équation ![]() , puis
, puis ![]() et on termine par
et on termine par ![]() .
.
![]() Si
Si ![]() , le système admet une infinité de solutions exprimées en fonction des inconnues
, le système admet une infinité de solutions exprimées en fonction des inconnues ![]() où
où ![]() : on résout l’équation
: on résout l’équation ![]() , puis
, puis ![]() et on termine par
et on termine par ![]() .
.
Remarque : si ![]() , le système
, le système ![]() admet une unique solution. Il est appelé système de Cramer.
admet une unique solution. Il est appelé système de Cramer.
Exemple
Résoudre dans ![]() selon la valeur de
selon la valeur de ![]() le système
le système
![]()
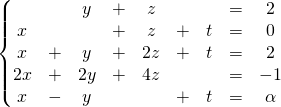 .
.
Correction :
La matrice associée à ce système est :
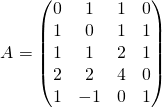
![]() Recherche d’un système équivalent au système
Recherche d’un système équivalent au système ![]() .
.
![]() Première opération :
Première opération : ![]() et le premier pivot est 1 :
et le premier pivot est 1 :
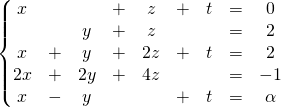 .
.
La matrice associée est
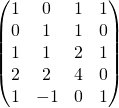
![]() Suppression de la variable
Suppression de la variable ![]() dans les lignes de numéro supérieur ou égal à 2 :
dans les lignes de numéro supérieur ou égal à 2 :
![]() ,
, ![]() et
et ![]()
On obtient le système équivalent
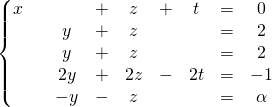 .
.
et la matrice associée est
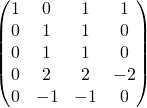
![]() Le pivot suivant est en ligne 2, colonne 2 , on supprime l’inconnue
Le pivot suivant est en ligne 2, colonne 2 , on supprime l’inconnue ![]() à partir de la troisième équation par les opérations
à partir de la troisième équation par les opérations
![]() ,
, ![]() et
et ![]()
On obtient le système équivalent :
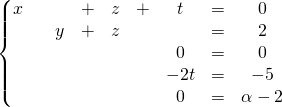 .
.
de matrice associée
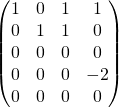
![]() On utilise
On utilise ![]()
![]() On obtient le système équivalent :
On obtient le système équivalent :
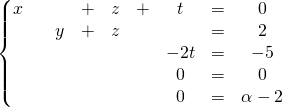 .
.
et la matrice associée est
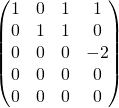
La transformation est terminée.
![]() Rang et discussion.
Rang et discussion.
On a obtenu 3 pivots en colonnes 1, 2 et 4 .
Le système est de rang 3.
Il est incompatible lorsque ![]() .
.
Il est compatible lorsque ![]() et dans ce cas il est équivalent au système
et dans ce cas il est équivalent au système
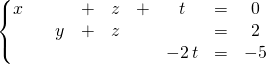 .
.
![]() ,
, ![]() et
et ![]() sont inconnues principales et
sont inconnues principales et ![]() est inconnue secondaire.
est inconnue secondaire.
![]() Fin de la résolution.
Fin de la résolution.
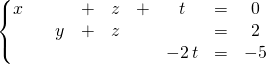 .
.
ssi 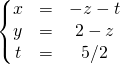
ssi 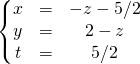
L’ensemble des solutions est l’ensemble des 4-uplets
![]() lorsque
lorsque ![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
4. Interprétation géométrique
4.1. Système réel de 2 équations à 2 inconnues
On suppose que le plan ![]() est rapporté au repère canonique noté
est rapporté au repère canonique noté ![]() .
.
![]() Si
Si ![]() ,
, ![]() est l’équation d’une droite
est l’équation d’une droite ![]() de
de ![]() orthogonale au vecteur
orthogonale au vecteur ![]() ou de vecteur directeur
ou de vecteur directeur ![]() .
.
![]() Si
Si ![]() et
et ![]() soit
soit ![]()
On note
![]() la droite d’équation
la droite d’équation ![]()
et ![]() la droite d’équation
la droite d’équation ![]() .
.
![]() Si
Si ![]() ,
, ![]() admet comme unique solution le point d’intersection des deux droites
admet comme unique solution le point d’intersection des deux droites ![]() et
et ![]() .
.
![]() Si les droites
Si les droites ![]() et
et ![]() sont parallèles (
sont parallèles (![]() ) et distinctes, le système
) et distinctes, le système ![]() n’a pas de solution.
n’a pas de solution.
![]() Si
Si ![]() soit s’il existe
soit s’il existe ![]() tel que
tel que ![]() , l’ensemble des solutions de
, l’ensemble des solutions de ![]() est l’ensemble des points de
est l’ensemble des points de ![]() .
.
4.2. Système réel de 3 équations à 3 inconnues
On suppose que l’espace ![]() est rapporté au repère canonique noté
est rapporté au repère canonique noté ![]() .
.
![]() Si
Si ![]() ,
,
![]()
est l’équation d’un plan ![]() de
de ![]() orthogonal au vecteur
orthogonal au vecteur ![]() .
.
![]() Soient
Soient ![]() ,
, ![]() et
et
![]() dans
dans ![]() tous distincts de
tous distincts de ![]() .
.
On note ![]() le plan d’équation
le plan d’équation ![]() .
.
On définit de même les plans ![]() et
et ![]() .
.
Soit ![]() :
:
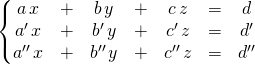
Résoudre le système ![]() revient à chercher l’intersection des trois plans
revient à chercher l’intersection des trois plans ![]() ,
, ![]() et
et ![]() .
.
On note ![]() le rang du système
le rang du système ![]()
On peut avoir
![]() un point (
un point (![]() ).
).
![]() une droite lorsque deux des plans sont non parallèles et le troisième a une équation combinaison linéaire des équations de ces deux plans.
une droite lorsque deux des plans sont non parallèles et le troisième a une équation combinaison linéaire des équations de ces deux plans.
(![]() et
et ![]() compatible).
compatible).
![]() un plan lorsque les trois plans sont confondus
un plan lorsque les trois plans sont confondus
(![]() et système compatible)
et système compatible)
![]() l’ensemble vide lorsque deux des trois plans sont parallèles et distincts (
l’ensemble vide lorsque deux des trois plans sont parallèles et distincts (![]() et système incompatible).
et système incompatible).
Les mathématiques sont une matière qu’il est nécessaire de réviser régulièrement pour voire une vraie progression. Les cours en ligne de Maths en Maths Sup, permettent ainsi d’aider les étudiants dans leurs révisions en dehors des cours en prépa. Vérifiez vos connaissances et travaillez sur vos difficultés en consultant quelques cours en ligne et nos cours de maths particulier au programme de Maths Sup :

