Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours sur les variables aléatoires en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
A. Variable aléatoire en Maths Sup MPSI, PCSI, MP2I, PTSI
1. Notations des variables aléatoires en Maths Sup
![]()
![]() est un espace probabilisé fini, une variable aléatoire réelle
est un espace probabilisé fini, une variable aléatoire réelle ![]() est une application de
est une application de ![]() dans
dans ![]() .
.
L’ensemble ![]() est un ensemble fini.
est un ensemble fini.
![]() Dans la suite, on note
Dans la suite, on note
![]()
![]() .
.
![]() Si
Si ![]() est une partie de
est une partie de ![]() ,
, ![]() .
.
![]()
![]()
![]() Si
Si ![]() ,
, ![]()
Ce sont des parties finies de ![]() .
.
![]() Si
Si ![]() est une variable aléatoire sur
est une variable aléatoire sur ![]() , si
, si ![]() , on peut définir la variable aléatoire notée
, on peut définir la variable aléatoire notée ![]() :
: ![]() .
.
2. Définir la loi d’une variable aléatoire en Maths Sup
![]() Donner la loi de la variable aléatoire
Donner la loi de la variable aléatoire ![]() ,
,
![]() c’est donner l’ensemble
c’est donner l’ensemble ![]()
![]() et définir
et définir ![]() .
.
On doit vérifier ![]() .
.
![]() On peut alors définir la loi
On peut alors définir la loi ![]() de
de ![]()
![]()
![]() .
.
Alors ![]() est un ensemble probabilisé fini.
est un ensemble probabilisé fini.
3. Définir l’espérance d’une variable aléatoire en Maths Sup
![]() Si
Si ![]() est une variable aléatoire sur
est une variable aléatoire sur ![]() et si
et si ![]() .
.
l’espérance de ![]() est le réel
est le réel ![]() .
.
![]()
![]() .
.
Cette formule peut être utile pour les démonstrations des propriétés de l’espérance, elle est inutile dans le cas des calculs pratiques.
![]() Si
Si ![]() , on peut calculer
, on peut calculer ![]() sans utiliser la loi de
sans utiliser la loi de ![]() grâce au théorème de transfert.
grâce au théorème de transfert.
Lorsque ![]() ,
,
![]() .
.
![]() En particulier si
En particulier si ![]() est une variable aléatoire réelle,
est une variable aléatoire réelle,
![]() lorsque
lorsque ![]() ,
, ![]()
![]() Si
Si ![]() et
et ![]() sont définies sur
sont définies sur ![]() à valeurs dans
à valeurs dans ![]() ,
,
![]()
![]() Si
Si ![]() ,
, ![]() .
.
![]() Si
Si ![]() , le moment d’ordre
, le moment d’ordre ![]() de
de ![]() est égal à
est égal à ![]() .
.
4. Définir la variance de  en Maths Sup
en Maths Sup
![]() Si
Si ![]() est une variable aléatoire réelle, la variance de
est une variable aléatoire réelle, la variance de ![]() est égale à
est égale à ![]() .
.
C’est un réel positif ou nul et l’écart type de ![]() est égal à
est égal à ![]() , il mesure la dispersion de
, il mesure la dispersion de ![]() autour de
autour de ![]() .
.
![]() Il vaut mieux calculer la variance de
Il vaut mieux calculer la variance de ![]() à l’aide du théorème de Koenig-Huyghens
à l’aide du théorème de Koenig-Huyghens
![]() .
.
![]() Si
Si ![]() est une variable aléatoire réelle, lorsque
est une variable aléatoire réelle, lorsque ![]() ,
, ![]()
![]() Si
Si ![]() , la variable aléatoire
, la variable aléatoire ![]() , appelée variable aléatoire centrée réduite associée à
, appelée variable aléatoire centrée réduite associée à ![]() , vérifie
, vérifie ![]() et
et ![]() .
.
5. Variables aléatoires de même loi en Maths Sup
Soient ![]() et
et ![]() deux variables aléatoires réelles définies sur
deux variables aléatoires réelles définies sur ![]() ont même loi lorsque
ont même loi lorsque
![]()
et ![]() ,
, ![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
B. Couples de variables aléatoires réelles en Maths Sup
1. Loi conjointe de variables aléatoire en Maths Sup
Soit ![]() un univers probabilisé fini.
un univers probabilisé fini.
![]() et
et ![]() sont deux variables aléatoires réelles sur
sont deux variables aléatoires réelles sur ![]() .
.
![]() Définir la loi conjointe des variables
Définir la loi conjointe des variables ![]() et
et ![]() , c’est donner
, c’est donner
![]()
![]()
et ![]()
![]()
![]() ,
,
la valeur de ![]() qui est aussi notée
qui est aussi notée ![]() .
.
![]() Vérifier que l’on a donné la loi du couple
Vérifier que l’on a donné la loi du couple ![]() , c’est vérifier que l’on a donné les ensembles
, c’est vérifier que l’on a donné les ensembles ![]() et
et ![]() et vérifier que
et vérifier que
![]() et
et ![]() ,
,
![]()
et ![]() .
.
2. Lois marginales de variables aléatoires en Maths Sup
![]() Ayant la loi conjointe des variables aléatoires
Ayant la loi conjointe des variables aléatoires ![]() et
et ![]() , on peut déterminer les lois des variables
, on peut déterminer les lois des variables ![]() et
et ![]() appelées lois marginales.
appelées lois marginales.
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
3. Loi conditionnelle de variable aléatoire en Maths Sup
Soient ![]() et
et ![]() deux variables aléatoires et
deux variables aléatoires et ![]() tel que
tel que ![]() ,
,
alors ![]()
![]()
définit la loi d’une variable aléatoire appelée loi conditionnelle de ![]() sachant
sachant ![]() .
.
4. Indépendance de deux variables aléatoires en Maths Sup
![]() Deux variables aléatoires
Deux variables aléatoires ![]() et
et ![]() définies sur
définies sur ![]() sont indépendantes lorsque
sont indépendantes lorsque
![]()
![]()
![]()
![]() Si
Si ![]() et
et ![]() sont indépendantes, pour tout
sont indépendantes, pour tout ![]() ,
, ![]()
![]() .
.
![]() Si
Si ![]() et
et ![]() sont indépendantes, les variables
sont indépendantes, les variables ![]() et
et ![]() sont aussi indépendantes.
sont aussi indépendantes.
![]() Si
Si ![]() et
et ![]() sont indépendantes, pour tout
sont indépendantes, pour tout ![]() tel que
tel que ![]() , la loi conditionnelle de
, la loi conditionnelle de ![]() sachant
sachant ![]() est la loi de
est la loi de ![]() .
.
5. Indépendance de  variables aléatoires en Maths Sup
variables aléatoires en Maths Sup
![]() variables aléatoires réelles
variables aléatoires réelles ![]() sont mutuellement indépendantes
sont mutuellement indépendantes
ssi ![]()
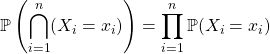
ssi ![]() ,
,
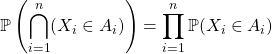
![]() Si
Si ![]() sont
sont ![]() v.a.r. mutuellement indépendantes, toute sous famille est formée de variables aléatoires indépendantes.
v.a.r. mutuellement indépendantes, toute sous famille est formée de variables aléatoires indépendantes.
En particulier, elles sont deux à deux indépendantes.
![]() Si
Si ![]() sont
sont ![]() v.a.r. indépendantes de loi de Bernoulli de paramètre
v.a.r. indépendantes de loi de Bernoulli de paramètre ![]() ,
, ![]() suit une loi binomiale de paramètres
suit une loi binomiale de paramètres ![]() et
et ![]() .
.
6. Compléments des propriétés de l’espérance en Maths Sup
![]() L’espérance est une forme linéaire sur l’espace vectoriel des variables aléatoires définies sur
L’espérance est une forme linéaire sur l’espace vectoriel des variables aléatoires définies sur ![]() .
.
![]() Si
Si ![]() est une variable aléatoire à valeurs positive sou nulles,
est une variable aléatoire à valeurs positive sou nulles, ![]()
![]() Soient
Soient ![]() et
et ![]() deux variables aléatoires telles que
deux variables aléatoires telles que ![]() ,
, ![]()
![]() Si
Si ![]() et
et ![]() sont deux variables aléatoires dont on connaît la loi conjointe,
sont deux variables aléatoires dont on connaît la loi conjointe, ![]() est égale à
est égale à
![]() .
.
![]() Si
Si ![]() et
et ![]() sont des v.a.r. sur
sont des v.a.r. sur ![]() indépendantes,
indépendantes, ![]() .
.
C. Les lois usuelles de variables aléatoires en Maths Sup
![]() Variable aléatoire constante :
Variable aléatoire constante :
![]()
![]() ,
, ![]() .
.
![]()
![]() et
et ![]() .
.
![]() Variable aléatoire de Bernoulli de paramètre
Variable aléatoire de Bernoulli de paramètre ![]() :
:
![]()
![]() ,
,
![]() et
et ![]()
![]()
![]() et
et ![]() .
.
On note ![]() .
.
![]() Variable aléatoire uniforme sur
Variable aléatoire uniforme sur ![]() :
:
![]()
![]() ,
,
![]()
![]()
![]() et
et ![]() (deux résultats à retrouver)
(deux résultats à retrouver)
On note ![]() .
.
![]() Variable aléatoire de loi binomiale de paramètres
Variable aléatoire de loi binomiale de paramètres ![]() et
et ![]() :
:
![]()
![]() ,
,
![]()
![]()
![]()
![]() et
et ![]() .
.
On note ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
D. Calculs pratiques de l’espérance ou de la variance en Maths Sup
![]() En reconnaissant la loi de
En reconnaissant la loi de ![]()
![]() Si
Si ![]() ,
, ![]() .
.
![]() En utilisant la définition et en utilisant les sommes classiques.
En utilisant la définition et en utilisant les sommes classiques.
![]() En utilisant le théorème de transfert qui rend inutile le calcul de la loi de
En utilisant le théorème de transfert qui rend inutile le calcul de la loi de ![]() lorsque l’on peut écrire
lorsque l’on peut écrire ![]() .
.
C’est souvent la démarche à utiliser lorsque l’on demande directement l’espérance de ![]() sans calculer sa loi, lorsque cette loi n’est pas classique.
sans calculer sa loi, lorsque cette loi n’est pas classique.
![]() En écrivant
En écrivant ![]() comme somme de variables aléatoires plus simples (en général des variables aléatoires de Bernoulli).
comme somme de variables aléatoires plus simples (en général des variables aléatoires de Bernoulli).
![]() On peut aussi envisager de déduire de
On peut aussi envisager de déduire de
![]() une relation permettant d’être réutilisée pour le calcul de
une relation permettant d’être réutilisée pour le calcul de ![]() .
.
2. Pour la variance des variables aléatoires en Maths Sup
![]() En reconnaissant la loi de
En reconnaissant la loi de ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
![]() En utilisant la formule de Koenig-Huyghens,
En utilisant la formule de Koenig-Huyghens, ![]()
![]() Il sera peut-être plus simple de passer par le calcul , pour
Il sera peut-être plus simple de passer par le calcul , pour ![]() , de
, de
![]() (en général
(en général ![]() ) et d’utiliser la formule :
) et d’utiliser la formule :
![]()
![]()
![]() En écrivant
En écrivant ![]() où l’on connaît la loi des variables
où l’on connaît la loi des variables ![]() et
et ![]() et en particulier si
et en particulier si ![]() et
et ![]() sont indépendantes,
sont indépendantes,
![]() .
.
![]() En écrivant
En écrivant ![]() comme somme de variables aléatoires
comme somme de variables aléatoires ![]() plus simples (en général des variables aléatoires de Bernoulli).
plus simples (en général des variables aléatoires de Bernoulli).
![]() si elles sont 2 à 2 indépendantes, la variance de
si elles sont 2 à 2 indépendantes, la variance de ![]() est la somme des variances des
est la somme des variances des ![]() .
.
E. Inégalités de Bienayme-Tchebichev en Maths Sup
![]() L’énoncé
L’énoncé
![]() Hypothèses :
Hypothèses : ![]() est une variable aléatoire sur l’univers fini
est une variable aléatoire sur l’univers fini ![]() et
et ![]() .
.
![]() Conclusion :
Conclusion : ![]() .
.
F. Des méthodes pour déterminer les lois de quelques variables
1. Cas de variables aléatoires à valeurs dans 
On suppose que ![]() est une variable aléatoire à valeurs dans
est une variable aléatoire à valeurs dans ![]() .
.
1.a. On a su calculer  pour
pour  .
.
![]()
![]() .
.
![]() Si
Si ![]() , écrire
, écrire
![]()
Les événements étant disjoints,
![]()
soit
![]()
1.b. On a su calculer  pour
pour  .
.
Lorsque ![]() ,
,
![]()
![]() .
.
![]() Si
Si ![]() , écrire
, écrire
![]()
Les événements étant disjoints,
![]()
soit
![]()
2. Somme de deux variables aléatoires en Maths Sup
Pour trouver la loi de ![]() lorsque
lorsque ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() .
.
![]() Déterminer
Déterminer ![]() .
.
![]() Écrire si
Écrire si ![]() ,
,
![]()
C’est une réunion d’événements deux à deux incompatibles,
![]() .
.
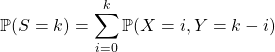
3. Minimum et maximum de deux variables aléatoires indépendantes
Si ![]() et
et ![]() sont deux variables réelles, on note
sont deux variables réelles, on note ![]() et
et ![]() .
.
![]() Lois de
Lois de ![]() et
et ![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
![]() Loi du couple
Loi du couple
![]()
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]()
![]()
![]() Si
Si ![]() .
.
Il est utile de se souvenir que
![]()
![]() et
et ![]() .
.
4. Maximum et minimum de  variables aléatoires réelles
variables aléatoires réelles
Si ![]() sont
sont ![]() variables aléatoires réelles, on note
variables aléatoires réelles, on note ![]() et
et ![]() .
.
![]() Loi de
Loi de ![]()
On calcule
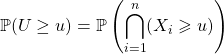
(On peut aussi utiliser ![]() ).
).
Si les variables sont à valeurs dans ![]() , on termine avec les remarques du 6.1.2.
, on termine avec les remarques du 6.1.2.
![]() Loi de
Loi de ![]()
On calcule
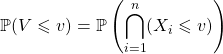 .
.
Si les variables ![]() sont à valeurs dans
sont à valeurs dans ![]() , on termine avec les remarques du 1.b.
, on termine avec les remarques du 1.b.
Retrouvez d’autres cours en ligne de maths et des cours particuliers maths à Lyon au programme de MPSI, PCSI et PTSI qui vous permettront d’améliorer vos résultats et votre moyenne en Maths Sup :

