Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Nombres complexes en MPSI, MP2I, PCSI, PTSI
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en Maths Sup
Ce cours en ligne sur les nombres complexes en prépa scientifique vous accompagnera tout au long de votre parcours en CPGE. Il est primordial de bien assimiler ce chapitre et de le comprendre de manière approfondie. N’hésitez pas demander de l’aide en cours de soutien de maths si vous trouvez des points bloquants.
Résumé de cours et méthodes – racines n-ième de 1, forme exponentielle
1. Pour traduire
![]() M1. Pour traduire que
M1. Pour traduire que ![]() est un réel, on écrit :
est un réel, on écrit : ![]() est réel ssi
est réel ssi ![]() .
.
M1B. Pour traduire que ![]() est un réel non nul, on peut aussi écrire :
est un réel non nul, on peut aussi écrire :![]() est un réel non nul ssi il existe
est un réel non nul ssi il existe ![]() tel que
tel que ![]() .
.
![]() M2. Pour traduire que
M2. Pour traduire que ![]() est un imaginaire pur, on écrit :
est un imaginaire pur, on écrit : ![]() est imaginaire pur ssi
est imaginaire pur ssi ![]() .
.
M2B. Pour traduire que ![]() est un imaginaire pur non nul, on peut aussi écrire :
est un imaginaire pur non nul, on peut aussi écrire :![]() est un imaginaire pur non nul ssi il existe
est un imaginaire pur non nul ssi il existe ![]() tel que
tel que ![]()
👍 Dans les deux cas, il est préférable pour ne pas alourdir les calculs de remplacer les complexes par leur forme cartésienne le plus tard possible (et même d’éviter si c’est possible d’introduire cette forme cartésienne).
![]() M3. Pour traduire que
M3. Pour traduire que ![]() est un complexe de module 1, le plus simple en général est d’écrire qu’il existe un réel
est un complexe de module 1, le plus simple en général est d’écrire qu’il existe un réel ![]() tel que
tel que ![]() .
.
Mais il peut être utile d’utiliser : si ![]() est un complexe de module 1 ,
est un complexe de module 1 , ![]() .
.
2. Utiliser les modules
![]() M1. Les complexes
M1. Les complexes ![]() ,
, ![]() et
et ![]() ont même module.
ont même module.![]() M2. Le module d’un produit de complexes est égal au produit des modules, le module d’un quotient de complexes est égal au quotient des modules.
M2. Le module d’un produit de complexes est égal au produit des modules, le module d’un quotient de complexes est égal au quotient des modules.![]() M3. Un complexe
M3. Un complexe ![]() est de module 1 si, et seulement si,
est de module 1 si, et seulement si, ![]() .
.![]() M4. Si
M4. Si ![]() est un complexe,
est un complexe, ![]() et
et ![]() .
.![]() M5. Inégalité triangulaire :
M5. Inégalité triangulaire :
si ![]() .
.
Il y a égalité ssi ![]() ou il existe
ou il existe ![]() .
. ![]() M6. Conséquence de l’inégalité triangulaire :
M6. Conséquence de l’inégalité triangulaire :
si ![]() .
.![]() M7. Pour tout complexe
M7. Pour tout complexe ![]() de module 1, il existe un réel
de module 1, il existe un réel ![]() (unique modulo
(unique modulo ![]() ) tel que
) tel que ![]() .
.![]() M8. L’ensemble
M8. L’ensemble ![]() des nombres complexes de module
des nombres complexes de module ![]() vérifie :
vérifie :![]()
![]() ,
, ![]() si
si ![]()
![]() si
si ![]() .
.
On dit que ![]() est un groupe.
est un groupe.
3. Pour calculer la forme trigonométrique d’un complexe
![]() M1. Lorsque l’on a obtenu
M1. Lorsque l’on a obtenu ![]() , ⚠️ ne pas conclure hâtivement :
, ⚠️ ne pas conclure hâtivement : ![]() si
si ![]() = 0,
= 0, ![]() = 0,
= 0, ![]() a un module nul, n’a pas d’argument,
a un module nul, n’a pas d’argument,![]() si
si ![]() ,
, ![]() et
et ![]() .
. ![]() si
si ![]() ,
, ![]() et
et ![]() .
.
![]() M2. On peut faire le calcul de
M2. On peut faire le calcul de ![]() , puis écrire
, puis écrire ![]() , alors il reste à trouver un réel
, alors il reste à trouver un réel ![]() tel que
tel que ![]() , c’est-à-dire à trouver un réel
, c’est-à-dire à trouver un réel ![]() tel que
tel que ![]() et
et ![]() .
.
![]() M3. Si
M3. Si ![]() n’est pas réel, on peut faire le calcul de
n’est pas réel, on peut faire le calcul de ![]() et dire qu’un argument de
et dire qu’un argument de ![]() est
est ![]() où
où ![]()
![]() si
si ![]()
![]()
![]() si
si ![]()
![]() M4. Lorsque
M4. Lorsque ![]() est un produit ou un quotient de deux complexes, il est souvent plus simple de calculer module et argument des deux facteurs du produit ou du quotient et d’appliquer les règles sur les modules et arguments des produits ou des quotients.
est un produit ou un quotient de deux complexes, il est souvent plus simple de calculer module et argument des deux facteurs du produit ou du quotient et d’appliquer les règles sur les modules et arguments des produits ou des quotients.
![]() M5. Lorsque
M5. Lorsque ![]() , appliquer la transformation indiquée en M1 du §4 et la méthode décrite en M1 de ce paragraphe.
, appliquer la transformation indiquée en M1 du §4 et la méthode décrite en M1 de ce paragraphe.
4. Pour simplifier
![]() M1. Pour simplifier lorsque
M1. Pour simplifier lorsque ![]() et
et ![]() sont réels,
sont réels, ![]() ou
ou ![]() ,
, ![]() 👍 on met en facteur » e puissance la demi- somme des exposants « ,
👍 on met en facteur » e puissance la demi- somme des exposants « ,
ce qui donne : ![]()
![]()
![]() ou l’on connaît par coeur les résultats :
ou l’on connaît par coeur les résultats : ![]()
![]()
![]() En particulier, il est conseillé de retenir les formule très utilisées :
En particulier, il est conseillé de retenir les formule très utilisées :
![]()
![]() .
.
![]() M2. Soient
M2. Soient ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() ne soit pas un multiple de
ne soit pas un multiple de ![]() .
.
Pour simplifier 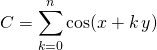 ou
ou 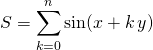 , on introduit
, on introduit 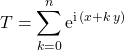 , on écrit que
, on écrit que ![]() et
et ![]() .
.
On calcule ![]() en écrivant
en écrivant 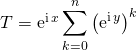 .
.
En notant ![]() , on utilise
, on utilise 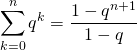 .On simplifie cette somme en utilisant la transformation décrite en M1.
.On simplifie cette somme en utilisant la transformation décrite en M1.
5. Pour calculer les racines carrées d’un complexe  non nul
non nul
![]() M1. Si l’on sait calculer la forme trigonométrique du complexe
M1. Si l’on sait calculer la forme trigonométrique du complexe ![]() ,
, ![]() où
où ![]() , les racines carrées de
, les racines carrées de ![]() sont les deux complexes :
sont les deux complexes : ![]() et
et ![]() .
.
![]() M2. Si l’on ne sait pas calculer la valeur d’un argument de
M2. Si l’on ne sait pas calculer la valeur d’un argument de ![]() , on calcule les racines carrées sous forme cartésienne, en cherchant
, on calcule les racines carrées sous forme cartésienne, en cherchant ![]() racine carrée de
racine carrée de ![]() sous la forme
sous la forme ![]() avec
avec ![]() solution du système :
solution du système :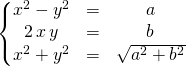
👍 la dernière équation étant obtenue en écrivant que ![]() .
.
Un cas simple : les racines carrées de ![]() où
où ![]() sont
sont ![]() et
et![]() .
.
⚠️ Important : la notation ![]() est réservée aux
est réservée aux ![]() éléments de
éléments de ![]() , il n’y a pas de notation pour les racines carrées du complexe
, il n’y a pas de notation pour les racines carrées du complexe ![]() non nul. Mais on peut dire que l’on note
non nul. Mais on peut dire que l’on note ![]() tel que
tel que ![]() pour signifier que
pour signifier que ![]() est une racine carrée de
est une racine carrée de ![]() .
.
👍 Les racines carrées de ![]() sont
sont ![]()
![]()
et ![]()
avec ![]() si
si ![]() et
et ![]() si
si ![]() .
.
6. Pour calculer les racines  -ièmes d’un complexe non nul
-ièmes d’un complexe non nul
Dans ce paragraphe, on suppose que ![]() .
.
⚠️ Important : un complexe non nul a toujours ![]() racines
racines ![]() -ièmes distinctes.
-ièmes distinctes.
Il n’y a pas de notation pour les racines ![]() -ièmes d’un complexe.
-ièmes d’un complexe.
Lorsque ![]() est pair, la notation
est pair, la notation ![]() est réservée aux réels
est réservée aux réels ![]() positifs ou nuls et lorsque
positifs ou nuls et lorsque ![]() est impair, la notation
est impair, la notation ![]() est réservée aux réels
est réservée aux réels ![]() .
.
![]() M1. On introduit la forme trigonométrique du complexe
M1. On introduit la forme trigonométrique du complexe ![]() :
: ![]() et on applique le résultat du cours :
et on applique le résultat du cours : ![]() admet
admet ![]() racines
racines ![]() -ièmes distinctes données par
-ièmes distinctes données par ![]() pour
pour ![]() ( mais on peut aussi prendre
( mais on peut aussi prendre ![]() valeurs consécutives entières de
valeurs consécutives entières de ![]() comme
comme ![]() ).
).
![]() M1.B. Dans le cas des racines
M1.B. Dans le cas des racines ![]() -ièmes de 1, il faut savoir que
-ièmes de 1, il faut savoir que ![]() avec
avec ![]() où
où ![]() .
.
L’ensemble des racines ![]() -ièmes de
-ièmes de ![]() est noté
est noté ![]() .
.
![]() M2. On connaît une racine
M2. On connaît une racine ![]() -ième du complexe
-ième du complexe ![]() soit par exemple
soit par exemple ![]() tel que
tel que ![]() , alors les racines
, alors les racines ![]() -ièmes de
-ièmes de ![]() sont obtenues en multipliant
sont obtenues en multipliant ![]() par les racines
par les racines ![]() -ièmes de
-ièmes de ![]() soit
soit ![]() avec
avec ![]() et
et ![]() .
.
exemples d’application
M2.1. Si ![]() est impair, une racine
est impair, une racine ![]() -ième de
-ième de ![]() est
est ![]() , donc les racines
, donc les racines ![]() -ièmes de
-ièmes de ![]() sont
sont ![]() avec
avec ![]()
![]() et
et ![]() .
.
M2.2. Si ![]() , les trois racines cubiques de
, les trois racines cubiques de ![]() dans
dans ![]() sont
sont ![]() avec
avec ![]() .
.
![]() M3. L’ensemble
M3. L’ensemble ![]() des racines
des racines ![]() -ièmes de
-ièmes de ![]() vérifie :
vérifie :![]()
![]()
![]() si
si ![]()
![]() si
si ![]() .
.
On dit que ![]() est un groupe.
est un groupe.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
7. Utilisation des racines  -ièmes de 1
-ièmes de 1
![]() M1. Cas des racines cubiques de 1 :
M1. Cas des racines cubiques de 1 :![]() ,
, ![]() ,
, ![]() .
.
Et bien sûr ![]() .
.![]() , donc
, donc ![]() et
et ![]() sont les racines de l’équation
sont les racines de l’équation ![]() .
.
![]() M2. Si
M2. Si ![]() sont les racines
sont les racines ![]() -ièmes de
-ièmes de ![]() , il faut savoir et savoir redémontrer que :
, il faut savoir et savoir redémontrer que :
Si 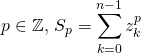 ,
, ![]()
![]() si
si ![]() est un multiple de
est un multiple de ![]()
![]()
![]() si
si ![]() n’est pas un multiple de
n’est pas un multiple de ![]()
![]() M3. Pour résoudre une équation du type
M3. Pour résoudre une équation du type ![]() où
où ![]() ,
, ![]() :
:![]() a) on examine le cas où
a) on examine le cas où ![]() s’annule,
s’annule, ![]() s’annule-t-il en même temps?
s’annule-t-il en même temps?![]() b) puis on se place dans le cas où
b) puis on se place dans le cas où ![]() ne s’annule pas, l’équation est alors équivalente à
ne s’annule pas, l’équation est alors équivalente à ![]() , soit à
, soit à ![]() est une racine
est une racine ![]() -ième de
-ième de ![]() .
.
On résout donc les ![]() équations obtenues
équations obtenues ![]() où
où ![]() est une racine
est une racine ![]() – ième de
– ième de ![]() .
.
8. équation du second degré à coefficients dans 
![]() M1. Résolution de
M1. Résolution de ![]() dans
dans ![]() , les coefficients
, les coefficients ![]() et
et ![]() étant complexes et
étant complexes et ![]() .
. ![]() On calcule
On calcule ![]() .
.
Mais il est alors hors de question(sauf si ![]() ) d’introduire la notation
) d’introduire la notation ![]()
On note ![]() une des racines carrées de
une des racines carrées de ![]() , soit
, soit ![]() ,
, ![]() se calcule en utilisant les méthodes indiquées en §4.
se calcule en utilisant les méthodes indiquées en §4.
![]() Les racines de l’équation sont alors
Les racines de l’équation sont alors ![]() et
et ![]() .
.
Elles sont distinctes ssi ![]() .
.
![]() On a
On a ![]() et
et ![]() .
.
👍 formules réduites :
Dans le cas où ![]() , on peut utiliser les formules du
, on peut utiliser les formules du ![]() réduit :
réduit :
On calcule ![]() , puis
, puis ![]() tel que
tel que ![]() , et les racines s’obtiennent par les formules :
, et les racines s’obtiennent par les formules :![]() et
et ![]() .
.
![]() M2.
M2. ![]() est une équation qu’il vaut mieux savoir résoudre très vite : elle admet pour racines
est une équation qu’il vaut mieux savoir résoudre très vite : elle admet pour racines ![]() et
et ![]() .
.
Les racines sont confondues ssi il existe ![]() tel que
tel que ![]() . Dans ce cas, elles sont réelles.
. Dans ce cas, elles sont réelles.
Sinon, les racines sont complexes conjuguées.
9. Utilisation de la fonction exponentielle complexe
![]() La définition :
La définition :
si ![]() où
où ![]()
![]()
![]() est un complexe non nul, de module
est un complexe non nul, de module ![]() et d’argument
et d’argument ![]() (modulo
(modulo ![]() ).
).
![]()
![]() ssi
ssi ![]()
![]() Si
Si ![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() si
si ![]() ,
, ![]() .
.
Formules de Moivre : Si ![]() ,
, ![]()
![]()
![]()
Si ![]() , l’ensemble des solutions de
, l’ensemble des solutions de ![]() est l’ensemble des complexes
est l’ensemble des complexes ![]()
où ![]() et
et ![]() est un argument de
est un argument de ![]() .
.
(ce résultat peut être retrouvé sans difficulté) .
10. Plan complexe et géométrie
10.1. Plan complexe
On appelle plan complexe ![]() un plan muni d’un repère orthonormal direct
un plan muni d’un repère orthonormal direct ![]() .
.
![]() À tout complexe
À tout complexe ![]() , on associe le point
, on associe le point ![]() de
de ![]() tel que
tel que ![]() . On dit que
. On dit que ![]() est l’image du complexe
est l’image du complexe ![]() et
et ![]() est l’affixe du point
est l’affixe du point ![]() .
.
À tout complexe ![]() , on peut associer le vecteur
, on peut associer le vecteur ![]() .
.
On dit que ![]() est l’affixe du vecteur
est l’affixe du vecteur ![]() .
.
![]() Si
Si ![]() est l’image de
est l’image de ![]() et
et ![]() est l’image de
est l’image de ![]() ,
, ![]() l’image
l’image ![]() de
de ![]() vérifie
vérifie ![]()
(![]() est un parallélogramme)
est un parallélogramme)![]() l’image
l’image ![]() de
de ![]() vérifie
vérifie ![]()
![]() Si
Si ![]() est l’affixe de
est l’affixe de ![]() ,
, ![]() et si
et si ![]() est l’affixe de
est l’affixe de ![]() ,
, ![]() .
.
![]() Si
Si ![]() et
et ![]() , l’ensemble des points
, l’ensemble des points ![]() d’affixe
d’affixe ![]() tels que
tels que ![]() est le cercle de centre
est le cercle de centre ![]() d’affixe
d’affixe ![]() et de rayon
et de rayon ![]() .
.
![]() Si
Si ![]() est un complexe non nul écrit sous la forme
est un complexe non nul écrit sous la forme ![]() ,
, ![]() est une mesure modulo
est une mesure modulo ![]() de l’angle orienté de vecteurs
de l’angle orienté de vecteurs ![]() .
.
10.2. Alignement et orthogonalité![]() M1. Si
M1. Si ![]() a pour affixe
a pour affixe ![]() ,
, ![]() a pour affixe
a pour affixe ![]() et
et ![]() a pour affixe
a pour affixe ![]() ,
,
si ![]() ,
, ![]()
![]() .
.
![]() M2. Soient
M2. Soient ![]() et
et ![]() trois points 2 à 2 distincts et
trois points 2 à 2 distincts et ![]() leurs affixes respectives,
leurs affixes respectives, ![]() M2.1.
M2.1. ![]() et
et ![]() sont alignés
sont alignés
ssi ![]()
ssi ![]() .
.
![]() M2.2.
M2.2. ![]()
ssi ![]()
ssi ![]() est un imaginaire pur (non nul).
est un imaginaire pur (non nul).
10.3. Transformations usuelles ![]() M1. Soit
M1. Soit ![]() , l’application
, l’application ![]() , de
, de ![]() dans
dans ![]() , qui au point
, qui au point ![]() d’affixe
d’affixe ![]() associe le point
associe le point ![]() d’affixe
d’affixe ![]() , est la translation de vecteur
, est la translation de vecteur ![]() d’affixe
d’affixe ![]() soit
soit ![]() .
.
![]() M2. L‘application
M2. L‘application ![]() , de
, de ![]() dans
dans ![]() , qui au point
, qui au point ![]() d’affixe
d’affixe ![]() associe le point
associe le point ![]() d’affixe
d’affixe ![]() , est la symétrie orthogonale par rapport à l’axe
, est la symétrie orthogonale par rapport à l’axe ![]()
Les points ![]() est
est ![]() sont symétriques par rapport à
sont symétriques par rapport à ![]() .
.
![]() M3. Si
M3. Si ![]() et
et ![]() ,
, ![]() l’équation
l’équation ![]() admet une unique solution
admet une unique solution ![]() .
. ![]() L’application
L’application ![]() , de
, de ![]() dans
dans ![]() , qui au point
, qui au point ![]() d’affixe
d’affixe ![]() associe le point
associe le point ![]() d’affixe
d’affixe ![]() est une similitude directe de centre
est une similitude directe de centre ![]() , de rapport
, de rapport ![]() et d’angle de mesure
et d’angle de mesure ![]() ,
,
c’est à dire ![]()
![]()
![]() si
si ![]() ,
, ![]() est défini par :
est défini par : ![]()
![]() et
et ![]() .
.
Cas particuliers :
1. ![]() est un réel non nul et différent de
est un réel non nul et différent de ![]()
![]() est une homothétie de centre
est une homothétie de centre ![]() et de rapport
et de rapport ![]() soit
soit ![]() .
.
2. Si ![]() ,
, ![]() est une rotation de centre
est une rotation de centre ![]() et d’angle
et d’angle ![]() .
.
👍 La rotation de centre ![]() et d’angle
et d’angle ![]() se traduit par
se traduit par ![]() avec
avec ![]() .
.
Révisez les chapitres à venir au programme de prépa en MPSI, PCSI et PTSI :

