Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Corrigés : Nombres complexes en MPSI, PCSI, PTSI
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en Maths Sup
Corrigés- nombres complexes en MPSI, PCSI, PTSI
1. Modules et arguments
Question 1 (Vrai/faux)
Le complexe non nul ![]() a pour argument
a pour argument ![]()
Corrigé :
Faux. ![]() Si
Si ![]() ,
, ![]() a un module égal à
a un module égal à ![]() et un argument congru à
et un argument congru à ![]() ,
,
![]() Si
Si ![]() , le module de
, le module de ![]() est égal à
est égal à ![]() , et son argument est congru à
, et son argument est congru à ![]() modulo
modulo ![]() car on écrit
car on écrit
![]() .
.
⚠️ à ne pas répondre trop vite en oubliant la discussion sur le signe de ![]() .
.
Question 2
a/ Si ![]() et
et ![]() sont des complexes,
sont des complexes, ![]()
Corrigé :
Vrai. ![]() En appliquant l’inégalité triangulaire :
En appliquant l’inégalité triangulaire : ![]()
![]()
donc ![]() .
.
![]() En échangeant
En échangeant ![]() et
et ![]() ,
, ![]()
et comme ![]() ,
, ![]()
En utilisant si ![]() et
et ![]() ,
, ![]() , on a donc prouvé l’inégalité.
, on a donc prouvé l’inégalité.
b/ Pour tout ![]() , montrer que
, montrer que ![]() .
.
Préciser les cas d’égalité
Corrigé :
![]() Démonstration de l’inégalité.
Démonstration de l’inégalité.
![]() On écrit
On écrit ![]() ,
,
donc ![]()
![]() En échangeant
En échangeant ![]() et
et ![]() et en utilisant
et en utilisant ![]() , on obtient
, on obtient
![]() .
.
![]() Par demi-somme des inégalités (1) et (2), on obtient :
Par demi-somme des inégalités (1) et (2), on obtient :
![]() .
.
![]() Il y a égalité ssi (1) et (2) sont des égalités ssi
Il y a égalité ssi (1) et (2) sont des égalités ssi
(![]() ou
ou ![]() avec
avec ![]() )
)
ou (![]() ou
ou ![]() avec
avec ![]() )
)
ssi ![]() ou
ou ![]() ssi
ssi ![]() .
.
I y a donc deux cas d’égalité si ![]() et un seul si
et un seul si ![]() .
.
Question 3
![]() est un imaginaire pur si, et seulement si,
est un imaginaire pur si, et seulement si,
a. ![]() .
.
b. ![]() est un réel négatif ou nul.
est un réel négatif ou nul.
Corrigé :
Question 4
Si ![]() ,
, ![]() et
et ![]() ont même partie réelle ssi
ont même partie réelle ssi ![]() .
.
Corrigé :
Faux car si ![]() , les parties réelles de
, les parties réelles de ![]() et
et ![]() sont nulles et
sont nulles et ![]() .
.
Si ![]() ,
, ![]()
![]() et
et ![]() ont même partie réelle ssi
ont même partie réelle ssi ![]() ssi
ssi ![]() ou
ou ![]() .
.
Question 5
Si ![]() et
et ![]() sont trois complexes de module
sont trois complexes de module ![]() ,
, ![]() .
.
Corrigé :
Vrai. Les 3 complexes ont pour module 1 donc ![]() ,
, ![]() et
et ![]() .
.
![]()
![]()
en réduisant au même dénominateur
![]()
![]()
car le module de ![]() est égal à 1.
est égal à 1.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Sur la fonction exponentielle
Question 1
Si ![]() est réel,
est réel, ![]()
Corrigé :
Vrai. ![]()
![]()
![]() est le conjugué de
est le conjugué de ![]() .
.
Question 2
Si ![]() est complexe,
est complexe, ![]() .
.
Corrigé :
Faux. Prendre ![]() .
.
![]() et
et ![]()
donc ![]() .
.
Question 3
Si ![]() est complexe,
est complexe, ![]() .
.
Corrigé :
Vrai. On écrit ![]() ,
, ![]() .
.
Puis on utilise ![]() et la croissance de la fonction exponentielle sur
et la croissance de la fonction exponentielle sur ![]() :
: ![]() .
.
Question 4
Si ![]() est un complexe non nul, les images des solutions de l’équation
est un complexe non nul, les images des solutions de l’équation ![]() sont alignées.
sont alignées.
Corrigé :
Vrai. On note ![]() où
où ![]() et
et ![]() .
.
On écrit ![]() avec
avec ![]() .
.
![]() ssi
ssi ![]()
ssi ![]() et
et ![]()
ssi ![]() et
et ![]() .
.
Les images des solutions sont alignées sur la droite d’équation ![]() .
.
2. Sur les racines  -ièmes
-ièmes
Question 1
Les racines ![]() – ièmes de
– ièmes de ![]() sont les complexes
sont les complexes ![]() où
où
a) ![]()
b) ![]()
c) ![]()
Corrigé :
La bonne réponse est c. On calcule les racines ![]() – ièmes d’un complexe non nul en utilisant
– ièmes d’un complexe non nul en utilisant ![]() valeurs consécutives entières de
valeurs consécutives entières de ![]() .
.
Seule la réponse c) donne ![]() valeurs entières consécutives de
valeurs entières consécutives de ![]() .
.
👍 Remarque : en général, on choisit les valeurs de ![]() entre
entre ![]() et
et ![]() . Mais il est possible de choisir comme ici
. Mais il est possible de choisir comme ici ![]() entre
entre ![]() et
et ![]() , ce qui permet alors de remarquer que si l’on note
, ce qui permet alors de remarquer que si l’on note ![]() ,
, ![]() ,
, ![]() et si
et si ![]()
![]() et
et ![]() sont conjugués.
sont conjugués.
Question 2
Si ![]() , il existe
, il existe ![]() ,
, ![]() .
.
Corrigé :
Faux. On note ![]() ;
; ![]()
S’il existait ![]() tel que
tel que ![]() , on aurait
, on aurait ![]() donc
donc ![]() .
.
Il existerait ![]() tel que
tel que ![]() alors
alors ![]() donc
donc ![]() ce qui est absurde.
ce qui est absurde.
👍 On rappelle la démonstration de ![]() .
.
Si l’on avait ![]() , il existerait
, il existerait ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() .
.
En écrivant ![]() et
et ![]() et en simplifiant par
et en simplifiant par ![]() , on peut se ramener au cas où
, on peut se ramener au cas où ![]() et
et ![]() ne sont pas tous les deux pairs ce que l’on suppose dans la suite.
ne sont pas tous les deux pairs ce que l’on suppose dans la suite.
Alors ![]() , donc
, donc ![]()
![]() est pair (car
est pair (car ![]() impair implique
impair implique ![]() impair).
impair).
On écrit ![]() et on simplifie par 2 :
et on simplifie par 2 :
![]() , donc
, donc ![]() est pair, ce qui contredit l’hypothèse sur
est pair, ce qui contredit l’hypothèse sur ![]() et
et ![]() .
.
On a prouvé que ![]() est irrationnel.
est irrationnel.
Question 3
Soit ![]() et
et ![]() .
.
![]() .
.
Corrigé :
Faux. ![]()
La propriété est fausse : par exemple, en prenant ![]() ,
, ![]() ne contient qu’un élément ou pour
ne contient qu’un élément ou pour ![]() avec
avec ![]() ,
, ![]() ,
, ![]() ne contient que 2 éléments.
ne contient que 2 éléments.
👍 Pour aller plus loin en MPSI (nécessite le cours d’arithmétique) :
![]() Dans le cas où
Dans le cas où ![]() avec
avec ![]() et
et ![]() premiers entre eux, alors
premiers entre eux, alors ![]() .
.
Il est évident que ![]() .
.
Pour prouver l’égalité, on démontre que ![]() a
a ![]() éléments.
éléments.
Soient ![]() tels que
tels que ![]() ,
, ![]()
On peut supposer par symétrie que ![]() .
.
Donc il existe ![]() tel que
tel que ![]()
![]()
donc ![]() .
.
![]() divise
divise ![]() et est premier avec
et est premier avec ![]() , donc
, donc ![]() divise
divise ![]() par le lemme de Gauss.
par le lemme de Gauss.
Comme ![]() ,
, ![]() et
et ![]() ,
, ![]() et est un multiple de
et est un multiple de ![]() .
.
On en déduit que ![]() .
.
On a donc prouvé que ![]() contient
contient ![]() éléments donc
éléments donc ![]() .
.
![]() Réciproquement si
Réciproquement si ![]() avec
avec ![]() , alors
, alors ![]() et
et ![]() sont premiers entre eux.
sont premiers entre eux.
En effet si ![]() ,
, ![]() , donc il existe
, donc il existe ![]() tel que
tel que ![]() soit
soit ![]() .
.
Il existe ![]() tel que
tel que ![]()
ce qui donne ![]() , donc par la relation de Bezout,
, donc par la relation de Bezout, ![]() et
et ![]() sont premiers entre eux.
sont premiers entre eux.
Conclusion
Soit ![]() et
et ![]() .
.
![]() ssi
ssi ![]() et
et ![]() sont premiers.
sont premiers.
Question 4
Soit ![]() ,
, ![]() .
.
Corrigé :
Vrai. Soit ![]()
![]() Il est évident que
Il est évident que ![]() .
.
![]() On note
On note ![]() .
.
On sait que ![]() .
.
![]() contient
contient ![]()
qui est l’ensemble des racines ![]() -ièmes de 1, car
-ièmes de 1, car ![]() prend
prend ![]() valeurs consécutives entières.
valeurs consécutives entières.
Donc ![]() .
.
Par double inclusion, ![]() .
.
Question 5
Soient ![]() .
.
![]() ssi
ssi ![]() divise
divise ![]() .
.
Corrigé :
Vrai. ![]() Si
Si ![]() divise
divise ![]() , on écrit
, on écrit ![]() avec
avec ![]() .
.
Si ![]() ,
, ![]() , donc
, donc ![]() .
.
On a prouvé que ![]() .
.
![]() On suppose que
On suppose que ![]() .
.
On note ![]()
alors ![]() donc
donc ![]() , il existe
, il existe ![]() tel que
tel que ![]() donc
donc ![]() et
et ![]() divise
divise ![]() .
.
Question 6
Soit ![]() . Il existe une bijection de
. Il existe une bijection de ![]() sur l’ensemble
sur l’ensemble ![]() des racines
des racines ![]() -ièmes de
-ièmes de ![]() .
.
Corrigé :
Vrai. On note ![]()
il est évident que ![]() .
.
Alors ![]() ,
,
où ![]()
et ![]() .
.
L’application ![]() ,
, ![]() est une bijection.
est une bijection.
Question 7
Si ![]() est impair,
est impair, ![]() .
.
Corrigé :
Vrai. On note ![]()
Comme ![]() ,
, ![]() , donc
, donc ![]() .
.
On note ![]() .
.
On sait que ![]() .
.
Alors ![]() .
.
Soient ![]() ,
,
![]() ssi
ssi ![]()
ssi ![]()
ssi ![]() .
.
Comme ![]() ,
, ![]() ,
,
on en déduit que ![]() ou
ou ![]() .
.
Si l’on avait ![]() , alors
, alors ![]() , donc
, donc ![]() est pair ce qui est exclu.
est pair ce qui est exclu.
On en déduit que ![]() et donc
et donc ![]() .
.
![]() contient donc
contient donc ![]() éléments distincts et est inclus dans
éléments distincts et est inclus dans ![]() qui a aussi
qui a aussi ![]() éléments, alors
éléments, alors ![]() .
.
Question 8
Les images ![]() des racines
des racines ![]() -ièmes de 1 sont les sommets d’un polygone régulier à
-ièmes de 1 sont les sommets d’un polygone régulier à ![]() côtés inscrit dans le cercle unité.
côtés inscrit dans le cercle unité.
Corrigé :
Vrai. On note ![]() où
où ![]() l’affixe de
l’affixe de ![]() .
.
On remarque que ![]() et
et ![]() où
où ![]() .
.
Si ![]() ,
, ![]()
Comme ![]() , les côtés du polygone ont même longueur égale à
, les côtés du polygone ont même longueur égale à ![]() , on obtient un polygone régulier et les sommets sont sur le cercle de centre
, on obtient un polygone régulier et les sommets sont sur le cercle de centre ![]() et de rayon
et de rayon ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Manipulation de complexes en maths sup
Exercice 1
Calculer les racines cubiques de ![]() . Les écrire sous forme cartésienne et en déduire la valeur de
. Les écrire sous forme cartésienne et en déduire la valeur de ![]() et
et ![]() .
.
Corrigé :
![]() admet comme racines cubiques les complexes :
admet comme racines cubiques les complexes :
![]()
![]()
et ![]() .
.
Comme ![]() ,
, ![]() .
.
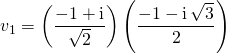
en égalant les parties réelles et imaginaires :
![]()
![]() .
.
Exercice 2
Si ![]() et
et ![]() sont deux complexes distincts de module 1,
sont deux complexes distincts de module 1,
![]() vérifie
vérifie ![]()
Corrigé :
On introduit des réels ![]() et
et ![]() tels que
tels que ![]() et
et ![]() (le coefficient 2 permet de simplifier les calculs qui suivent en évitant les facteurs
(le coefficient 2 permet de simplifier les calculs qui suivent en évitant les facteurs ![]() ) :
) :
![]()
![]()
![]()
et ![]()
![]()
![]() .
.
On note ![]() .
.
![]()
![]()
![]()
On note ![]() . Alors
. Alors
![]()
![]() où
où ![]() .
.
Donc ![]() est un imaginaire pur, son carré est négatif ou nul.
est un imaginaire pur, son carré est négatif ou nul.
Exercice 3
Résoudre le système ![]() et
et ![]() .
.
Corrigé :
![]() Résolution de la première équation
Résolution de la première équation
en notant ![]() :
:
![]()
![]()
![]()
![]() Résolution de la deuxième équation
Résolution de la deuxième équation
en notant ![]() ,
,
![]()
![]()
![]()
en multipliant par la quantité conjuguée
![]()
![]()
![]()
![]()
![]() .
.
La première équation donnait ![]() .
.
La relation sur les arguments devient alors
![]() et
et ![]()
![]()
Le système admet une seule solution égale à ![]() .
.
Exercice 4
Question 1
Soient deux complexes ![]() et
et ![]() .
.
![]()
Corrigé :
les termes
ce qui justifie la relation.
Question 2
Interprétation géométrique du résultat de la question 1 lorsque ![]() et
et ![]() sont non nuls.
sont non nuls.
Corrigé :
On note ![]() (resp.
(resp. ![]() ) le point d’affixe
) le point d’affixe ![]() (resp.
(resp. ![]() ).
).
Le point ![]() d’affixe
d’affixe ![]() est tel que
est tel que ![]() soit un parallélogramme.
soit un parallélogramme.
Le point ![]() d’affixe
d’affixe ![]() est tel que
est tel que ![]() .
.
On a établi que ![]()
Dans un parallélogramme, la somme des carrés des longueurs des 4 côtés est égale à la somme des carrés des longueurs des deux diagonales.
Question 3
On suppose que ![]() et on note
et on note ![]() une racine carrée de
une racine carrée de ![]() .
.
![]()
![]()
Corrigé :
On note ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() et
et ![]() , alors
, alors ![]() .
.
On peut supposer grâce à la symétrie du problème que ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
d’après la question 1.
![]()
![]() .
.
La relation est vérifiée pour ![]() .
.
5. Modules et arguments
Exercice 1
a) Trouver la forme trigonométrique du complexe :
 où
où ![]() .
.
Corrigé :
![]()
![]()
donc ![]()
On rappelle que ![]() .
.
![]() .
.
![]()
![]()
donc ![]()
On rappelle que ![]() .
.
![]() .
.
![]() On note
On note ![]()
![]()
![]()
![]()
![]() a pour module :
a pour module : ![]() et pour argument
et pour argument ![]() .
.
![]() On calcule
On calcule ![]() .
.
![]()
![]()
![]()
![]()
donc ![]() en utilisant la quantité conjuguée.
en utilisant la quantité conjuguée.
![]() Autre méthode :
Autre méthode :
On peut montrer que ![]() .
.
En notant ![]() et en utilisant
et en utilisant ![]() ,
,
on obtient ![]() donc
donc ![]() .
.
L’équation ![]() admet deux racines dont une seule est positive :
admet deux racines dont une seule est positive : ![]() .
.
![]() .
.
b/ Trouver la forme trigonométrique du complexe
![]()
si ![]() et
et ![]() .
.
Corrigé :
![]()
donc ![]()
![]() si
si ![]() soit si
soit si ![]() ,
, ![]() n’a pas d’argument.
n’a pas d’argument.
![]() si
si ![]() ,
, ![]() ,
,
![]() admet
admet ![]() pour module et
pour module et ![]() pour argument.
pour argument.
![]() si
si ![]() ,
, ![]() ,
,
… si ![]() est pair,
est pair, ![]() admet
admet ![]()
pour module et ![]() pour argument.
pour argument.
… si ![]() est impair, le module de
est impair, le module de ![]() est
est ![]() et son argument est
et son argument est ![]() .
.
Exercice 2
Soit ![]() un réel.
un réel.
On note ![]() .
.
On note ![]() et
et ![]() les racines de l’équation
les racines de l’équation ![]() .
.
Question 1
Sans calculer explicitement ![]() et
et ![]() , comparer leurs modules et leurs arguments.
, comparer leurs modules et leurs arguments.
Corrigé :
Comme ![]() , alors
, alors ![]() donc les modules sont inverses l’un de l’autre
donc les modules sont inverses l’un de l’autre
puis ![]() , les arguments sont opposés.
, les arguments sont opposés.
Question 2
Déterminer ![]() pour que
pour que ![]() et
et ![]() soient réels, puis pour qu’ils soient imaginai- res purs.
soient réels, puis pour qu’ils soient imaginai- res purs.
Corrigé :
![]() Si
Si ![]() et
et ![]() sont réels,
sont réels, ![]() est réel, donc
est réel, donc ![]() , donc
, donc ![]()
Réciproquement si ![]() , l’équation
, l’équation ![]() admet une racine double égale à 1, et si
admet une racine double égale à 1, et si ![]() , elle a dune racine double égale à
, elle a dune racine double égale à ![]() .
.
Conclusion :
Les racines sont réelles ssi ![]() .
.
![]() Si
Si ![]() et
et ![]() sont imaginaires purs ,
sont imaginaires purs , ![]() est imaginaire pur, donc
est imaginaire pur, donc ![]() , donc
, donc ![]() .
.
Réciproquement
![]() si
si ![]() , les racines de l’équation
, les racines de l’équation ![]()
sont ![]() et
et ![]() et sont imaginaires pures
et sont imaginaires pures
![]() si
si ![]() , les racines de l’équation
, les racines de l’équation ![]() sont
sont ![]() et
et ![]() et sont imaginaires pures
et sont imaginaires pures
Conclusion :
Les racines sont imaginaires pures ssi ![]() .
.
Question 3
Calculer les modules et arguments de ![]() et
et ![]() .
.
Corrigé :
On écrit ![]() .
.
![]()
![]()
![]() .
.
On est donc amené à discuter selon le signe de ![]() .
.
![]() Si
Si ![]() , on a une racine double égale à
, on a une racine double égale à ![]() car
car ![]() ,
,
donc de module égal à 1 et d’argument nul (resp . égal à ![]() ) si
) si ![]() (resp.
(resp. ![]() ).
).
![]() Si
Si ![]() , on se ramène au cas où
, on se ramène au cas où
![]()
![]() .
.
Leur module commun est ![]() , les arguments respectifs
, les arguments respectifs ![]() et
et ![]() .
.
![]() Si
Si ![]() , on se ramène au cas où
, on se ramène au cas où
![]()
![]() .
.
Leur module commun est ![]() , les arguments respectifs
, les arguments respectifs ![]() et
et ![]() .
.
Question 4
Si ![]() ,
, ![]() et
et ![]() ont même module à exprimer en fonction de
ont même module à exprimer en fonction de ![]() .
.
Corrigé :
Dans le cas où ![]() ,
,
![]()
et ![]()
![]()
or ![]()
![]()
![]()
et ![]()
donc ![]()
![]()
![]()
![]()
![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
4. Équations
Exercice 1
Résoudre dans ![]() :
:
![]() .
.
Corrigé :
![]() On calcule le discriminant de l’équation
On calcule le discriminant de l’équation
![]()
![]()
![]() .
.
![]() Puis l’on détermine les racines carrées de
Puis l’on détermine les racines carrées de ![]() en cherchant des réels
en cherchant des réels ![]() et
et ![]() tels que
tels que ![]() , pour cela on égale les parties réelles et imaginaires de cette relation, et en écrivant que le module de
, pour cela on égale les parties réelles et imaginaires de cette relation, et en écrivant que le module de ![]() (soit le carré du module de
(soit le carré du module de ![]() ) est égal au module de
) est égal au module de ![]() , on obtient le système:
, on obtient le système:
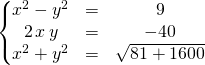
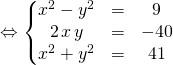
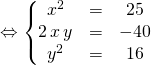
On obtient ![]()
donc ![]() avec
avec ![]()
![]() Les racines de l’équation sont
Les racines de l’équation sont ![]()
et ![]() .
.
Exercice 2
Résoudre ![]() .
.
Corrigé :
![]() On pose
On pose ![]() et on résout l’équation du second degré (1)
et on résout l’équation du second degré (1)
![]() .
.
Son discriminant réduit est égal à
![]()
![]()
on cherche les racines carrées de ![]() soit
soit ![]() avec
avec ![]() tel que
tel que ![]()
donc on résout le système :

ssi ![]() et
et ![]()
alors ![]()
et ![]() vérifie
vérifie ![]()
Les solutions de l’équation (1) sont
![]()
et ![]()
![]() On résout
On résout ![]() .
.
En posant ![]() , on résout le système
, on résout le système
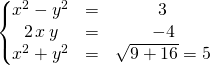
ssi ![]() et
et ![]() .
.
On obtient les deux premières racines ![]() et
et ![]() .
.
![]() On résout
On résout ![]() .
.
En posant ![]() , on résout le système
, on résout le système
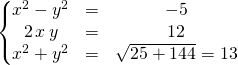
ssi ![]() et
et ![]() .
.
On obtient les deux dernières racines ![]() et
et ![]() .
.
Les 4 racines de l’équation sont
![]() et
et ![]() .
.
Exercice 3
Résoudre lorsque ![]() est un complexe, l’équation
est un complexe, l’équation
![]() .
.
Corrigé :
![]() On pose
On pose ![]() et on résout l’équation
et on résout l’équation
![]() dont on a une factorisation évidente :
dont on a une factorisation évidente :
![]() ssi
ssi ![]() ou
ou ![]() .
.
Les racines cubiques de ![]() sont donc
sont donc ![]() ,
, ![]() et
et ![]() .
.
Il reste 4 équations à résoudre
![]()
![]()
![]()
![]() où
où ![]() .
.
![]()
![]()
![]()
![]() où
où ![]() .
.
![]()
![]()
![]()
![]() où
où ![]() .
.
![]()
![]()
![]()
![]() où
où ![]() .
.
Les solutions sont les complexes
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
où ![]() .
.
Exercice 4
Résoudre dans ![]() l’équation
l’équation
![]() ,
,
où ![]() et
et ![]() .
.
Corrigé :
On pose ![]() et on commence par résoudre l’équation ainsi obtenue :
et on commence par résoudre l’équation ainsi obtenue :
(E’) ![]()
![]()
![]() .
.
L’équation (E’) a deux racines (éventuellement confondues) :
![]()
![]()
et ![]()
![]()
Il reste à calculer les racines nièmes de ![]() et
et ![]() en utilisant le résultat de cours.
en utilisant le résultat de cours.
Les racines de l’équation ![]() sont donc
sont donc ![]() et
et ![]() où
où ![]() .
.
Exercice 5
Oral Mines Telecom MP 2018
Résoudre l’équation ![]() sachant qu’elle a une racine réelle.
sachant qu’elle a une racine réelle.
Que dire du triangle formé par les images des trois racines ?
Corrigé :
![]() On cherche une solution réelle
On cherche une solution réelle ![]() en séparant partie réelle et partie imaginaire de l’équation, on obtient les CNS :
en séparant partie réelle et partie imaginaire de l’équation, on obtient les CNS :
![]()
![]() ,
,
3 n’est pas racine de la première équation, mais ![]() , donc
, donc ![]() est racine réelle de l’équation.
est racine réelle de l’équation.
![]() On cherche des complexes
On cherche des complexes ![]() et
et ![]() tels que
tels que
![]()
![]()
s’écrive ![]()
![]()
par égalité de deux fonctions polynômes, on obtient les CNS :
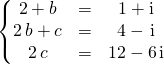
ce qui donne ![]() et
et ![]() .
.
![]() On résout
On résout ![]() .
.
On calcule le discriminant :
![]() .
.
On cherche ![]() et
et ![]() réels tels que
réels tels que ![]()
ce qui donne le système :
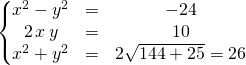
on obtient ![]() ,
, ![]() et
et ![]() .
.
Donc ![]() .
.
Les deux autres racines de l’équation sont
![]()
et ![]() .
.
![]() On note
On note ![]() ,
, ![]() et
et ![]()
![]() donc
donc ![]() soit
soit ![]()
![]()
![]()
donc ![]() .
.
Le triangle ![]() est rectangle isocèle en
est rectangle isocèle en ![]() .
.
Exercice 6
Question 1
Quel est l’ensemble des nombres complexes ![]() tels que
tels que ![]() ?
?
Corrigé :
![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]() est imaginaire pur.
est imaginaire pur.
Question 2
Pour tout ![]() , l’équation
, l’équation ![]() n’a pas de solution.
n’a pas de solution.
Corrigé :
Si ![]() est solution de
est solution de ![]() alors
alors ![]()
donc ![]()
et alors ![]() est imaginaire pur.
est imaginaire pur.
L’équation s’écrit
![]() où
où ![]() et
et ![]()
ssi ![]()
ssi ![]()
![]() Si
Si ![]() est pair,
est pair, ![]() et tout
et tout ![]() est solution.
est solution.
Donc l’ensemble des solutions est l’ensemble des imaginaires purs.
![]() Si
Si ![]() est impair, l’équation est équivalente à
est impair, l’équation est équivalente à ![]() ssi
ssi ![]() ssi
ssi ![]() ce qui est impossible si
ce qui est impossible si ![]()
L’équation n’admet pas de solution si ![]() est impair.
est impair.
Exercice 7
Soit ![]() ,
, ![]() et
et ![]()
Résoudre l’équation ![]() :
: ![]() .
.
Corrigé :
![]() 1 n’est pas racine de l’équation
1 n’est pas racine de l’équation ![]() ,
, ![]() est donc équivalente par quotient à
est donc équivalente par quotient à
![]() soit à
soit à ![]() est une racine
est une racine ![]() ième de
ième de ![]() c’est à dire égal à l’un des complexes
c’est à dire égal à l’un des complexes ![]() où
où ![]() avec
avec ![]() .
.
![]() Il reste donc à résoudre lorsque
Il reste donc à résoudre lorsque ![]() , l’équation
, l’équation ![]() qui est équivalente à
qui est équivalente à ![]() soit à
soit à ![]() .
.
![]() On examine ensuite s’il existe un entier
On examine ensuite s’il existe un entier ![]() tel que
tel que ![]() (dans ce cas, l’équation précédente est impossible) :
(dans ce cas, l’équation précédente est impossible) :
![]()
![]() .
.
On détermine la valeur de ![]() en remarquant que
en remarquant que ![]() et
et ![]() , donc
, donc ![]() .
.
Le seul multiple impair de ![]() dans cet intervalle est
dans cet intervalle est ![]() , donc
, donc ![]() et
et
![]()
![]() .
.
On discute ensuite cette équation :
![]() si
si ![]() , cette relation n’est pas vérifiée, donc
, cette relation n’est pas vérifiée, donc ![]() et toute valeur de
et toute valeur de ![]() convient.
convient.
![]() si
si ![]() et si
et si ![]() est impair, il est impossible d’avoir
est impair, il est impossible d’avoir ![]() et donc
et donc ![]() pour tout
pour tout ![]() .
.
![]() si
si ![]() et si
et si ![]() est pair (
est pair (![]() ), lorsque
), lorsque ![]() et cette valeur de
et cette valeur de ![]() doit être écartée.
doit être écartée.
![]() si
si ![]() et si
et si ![]() est pair, il est impossible d’avoir
est pair, il est impossible d’avoir ![]() et donc
et donc ![]() pour tout
pour tout ![]() .
.
![]() si
si ![]() et si
et si ![]() est impair (on écrit
est impair (on écrit ![]() ), lorsque
), lorsque ![]() et cette valeur de
et cette valeur de ![]() doit être écartée.
doit être écartée.
En résumé, Si ![]()
on note
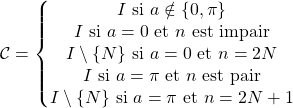
![]() Dans la suite, on suppose que
Dans la suite, on suppose que ![]() .
.
![]()
On rappelle que ![]() où
où ![]()
et que ![]()
et ![]()
donc ![]() .
.
Conclusion :
Les racines de ![]() sont les complexes
sont les complexes
![]() où
où ![]() .
.
D’autres cours en ligne et exercices de Maths pour les MPSI, PCSI et PTSI sont également consultables :

