Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Corrigés : Sommes et produits
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en Maths Sup
Corrigés – sommes et produits MPSI, PCSI
1. QCM – Vrai/Faux
Les relations suivantes sont- elles vraies ? Les corriger lorsqu’elles sont fausses.
Question 1
Si ![]() ,
, 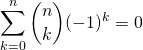 .
.
Corrigé :
L’affirmation est vraie si ![]() et fausse pour
et fausse pour ![]() .
.
Par le binôme de Newton,
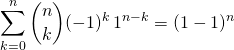 .
.
Le résultat est nul si ![]() et égal à 1 si
et égal à 1 si ![]() .
.
Question 2
Si ![]() ,
, 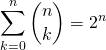 .
.
Corrigé :
Vrai. Par le binôme de Newton,
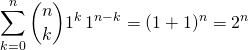 .
.
Question 3
Soit ![]() .
. 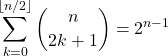 .
.
Corrigé :
Faux. La réponse correcte est
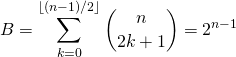 .
.
Par le binôme de Newton,
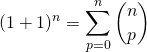
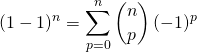 .
.
Par différence,
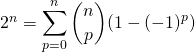
Il ne reste que les termes pour ![]() avec
avec ![]() , donc
, donc
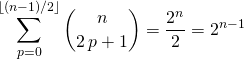 .
.
![]() \$
\$
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Question 4
Soit ![]() .
. 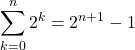 .
.
Corrigé :
Vrai. On utilise si ![]() ,
, 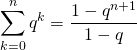
Question 5
Si ![]() et
et ![]() ,
, 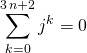 .
.
Corrigé :
Vrai. On utilise si ![]() ,
,
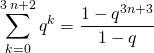
et ![]() .
.
Question 6
Soient ![]() et
et ![]() une famille de complexes.
une famille de complexes.
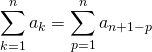 .
.
Corrigé :
Vrai. En posant ![]() soit
soit ![]() , lorsque
, lorsque ![]() varie de
varie de ![]() à
à ![]() ,
, ![]() varie de
varie de ![]() à
à ![]()
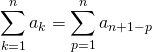 .
.
Question 7
Soient ![]() et
et ![]() une suite réelle ou complexe.
une suite réelle ou complexe.
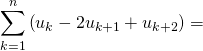
![]() .
.
Corrigé :
Faux. On pose ![]() .
.
On remarque que ![]()
puis on utilise un télescopage :
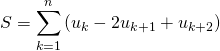
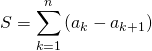
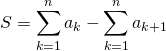
en posant ![]() ,
,
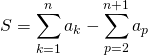
![]()
![]() .
.
Question 8
Soient ![]() et
et ![]() une suite réelle ou complexe.
une suite réelle ou complexe.
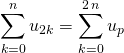 .
.
Corrigé :
Faux (sauf si les termes ![]() sont tous nuls).
sont tous nuls).
On a ajouté dans la somme tous les termes d’indices ![]() avec
avec ![]() .
.
👍 On retiendra qu’il est impossible d’utiliser un changement d’indice ![]() ou
ou ![]() .
.
Question 9
Soit ![]() .
. 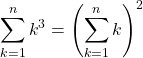 .
.
Corrigé :
L’affirmation est vraie car
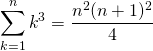
et 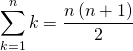 .
.
Question 10
Si ![]() ,
,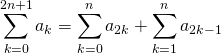
Corrigé :
Faux. 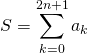
On sépare les indices ![]() avec
avec ![]() des indices
des indices ![]() avec
avec ![]() ssi
ssi ![]()
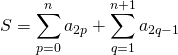
Question 11
Soient ![]() et
et ![]() ,
, ![]() deux familles réelles ou complexes
deux familles réelles ou complexes
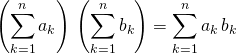 .
.
Corrigé :
Faux car il manque les termes ![]() si
si ![]()
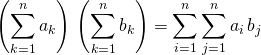
👍 Pour éviter une telle erreur prendre la précaution d’utiliser des indices différents dans les deux sommes :
c’est à dire écrire
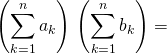
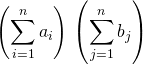 .
.
Question 12
Soit ![]() ,
, 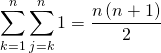
Corrigé :
Vrai. 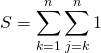
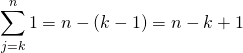
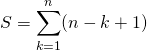
en posant ![]() qui varie de
qui varie de ![]() à
à ![]() si
si ![]() varie de
varie de ![]() à
à ![]() :
:
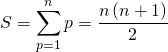 .
.
Question 13
Si 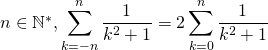
Corrigé :
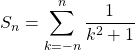
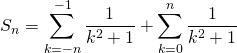
en posant ![]() dans la première somme
dans la première somme
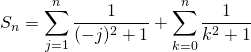
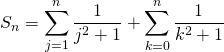
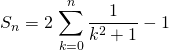 .
.
Question 14
Soit ![]() .
.
Si 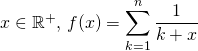 .
.
a) Si ![]() ,
, 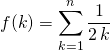 .
.
Corrigé :
Faux. ⚠️ Si l’expression ![]() est exprimée à l’aide d’un signe
est exprimée à l’aide d’un signe ![]() ou
ou ![]() , pour calculer
, pour calculer ![]() où
où ![]() est un entier,
est un entier, ![]() ne doit pas être l’indice de sommation ou de produit. Si nécessaire, changer le nom de l’indice de sommation ou de produit.
ne doit pas être l’indice de sommation ou de produit. Si nécessaire, changer le nom de l’indice de sommation ou de produit.
Il faut noter aussi que la relation proposée n’a pas de sens : dans ![]() , l’entier
, l’entier ![]() est fixé alors que dans la somme, il est variable !
est fixé alors que dans la somme, il est variable !
On écrit donc 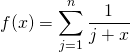
donc 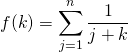
en posant ![]() ,
, 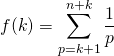 .
.
b) ![]() .
.
Faux. La question précédente donne 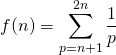 .
.
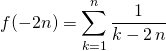
en posant ![]() ,
, ![]() varie de
varie de ![]() à
à ![]() lorsque
lorsque ![]() varie de
varie de ![]() à
à ![]() .
.
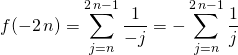
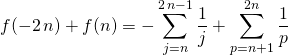
![]() .
.
Question 15
Soient ![]() et
et ![]() une famille réelle ou complexe.
une famille réelle ou complexe.
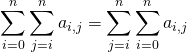 .
.
Corrigé :
Faux et n’a d’ailleurs pas de sens, la somme « extérieure » est impossible à calculer car ![]() n’est pas défini.
n’est pas défini.
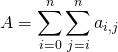
est écrite sous la forme d’une seule somme : ![]()
Puis ![]() étant fixé dans
étant fixé dans ![]() ,
, ![]() doit alors varier de
doit alors varier de ![]() à
à ![]() :
:
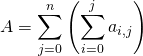 .
.
Par contre, on peut intervertir les sommes dans le cas :
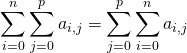
même si ![]() .
.
Question 16
Soient ![]() et
et ![]() et
et ![]() des complexes
des complexes
![]()
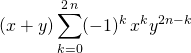 .
.
Corrigé :
On utilise la formule de Bernoulli en remarquant que
![]() avec
avec ![]() et
et ![]() .
.
On obtient :
![]()
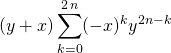
Question 17
Soient ![]() et
et ![]() des entiers tels que
des entiers tels que ![]() ,
, 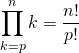
Corrigé :
on a 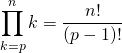
car 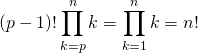 .
.
Question 18
Soient ![]() et
et ![]() des entiers tels que
des entiers tels que ![]() ,
, ![]() et
et![]() une famille de complexes.
une famille de complexes.
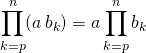 .
.
Corrigé :
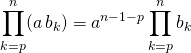
2. Des sommes et des coefficients du binôme
Exercice 1
Si ![]() , calculer
, calculer 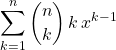
et 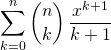 .
.
Corrigé :
![]() En dérivant
En dérivant ![]() telle que
telle que 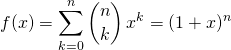 ,
,
on obtient
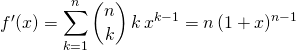
![]() Puis par intégration,
Puis par intégration,
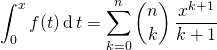
et ![]()
donc 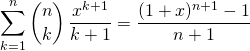 .
.
Exercice 2
Appliquer la formule du triangle de Pascal pour calculer 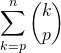 lorsque
lorsque ![]() .
.
Corrigé :
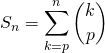 .
.
Par la formule du triangle de Pascal (valable si ![]() ),
),
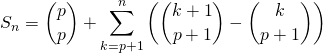
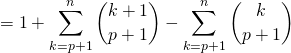
avec ![]() ,
,
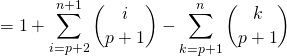
![]()
Exercice 3
Démontrer par récurrence que si ![]() ,
, 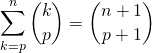 .
.
Corrigé :
On note si ![]()
![]() :
: 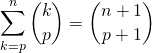 .
.
![]() Pour
Pour ![]() , la propriété est évidente car elle s’écrit
, la propriété est évidente car elle s’écrit ![]() .
.
![]() On suppose qu’elle est vraie au rang
On suppose qu’elle est vraie au rang ![]() . Par l’hypothèse de récurrence,
. Par l’hypothèse de récurrence,
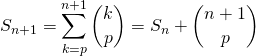
![]()
On termine par la formule du triangle de Pascal : ![]() .
.
La propriété est vraie au rang ![]() . Elle a été démontrée par récurrence.
. Elle a été démontrée par récurrence.
Exercice 4
Utiliser 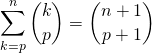 pour calculer
pour calculer![]() ,
, ![]() et
et ![]() .
.
Corrigé :
![]() En prenant
En prenant ![]() ,
, 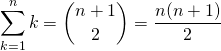 .
.
![]() En prenant
En prenant ![]() ,
,
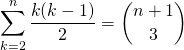
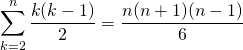
On peut commencer la somme à ![]() car le terme est nul pour
car le terme est nul pour ![]()
On obtient après multiplication par 2 :
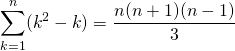
soit 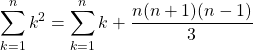
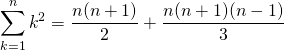
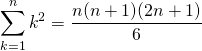 .
.
![]() En prenant
En prenant ![]() ,
,
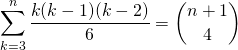
![]()
On commence la somme à ![]() car le terme est nul pour
car le terme est nul pour ![]() et
et ![]() .
.
On obtient après multiplication par 6 :
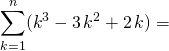
![]()
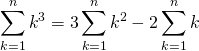
![]()

![]()
Après calculs :
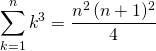 .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Des calculs de sommes
Exercice 1
Si ![]() ,
, 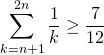 .
.
Corrigé :
Vrai. ![]()
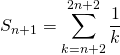
![]()
![]()
![]()
La suite ![]() est strictement croissante.
est strictement croissante.
![]()
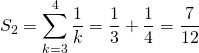 .
.
Pour tout ![]() .
.
Exercice 2
Soit ![]() .
.
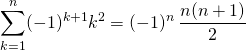
Corrigé :
Vrai. Si ![]() on note
on note 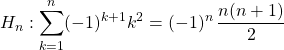
![]() Pour
Pour ![]()
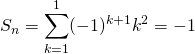
![]()
la propriété est vraie.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
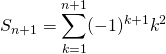
![]()
En utilisant ![]() :
: ![]() est égal à
est égal à
![]()
![]()
![]()
ce qui justifie ![]() .
.
La propriété est démontrée par récurrence.
Exercice 3
Soit ![]() .
.
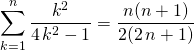
Corrigé :
Vrai. Si ![]() , on note
, on note
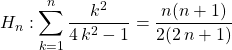 .
.
![]() Pour
Pour ![]() ,
,
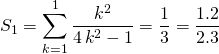
donc ![]() est démontrée.
est démontrée.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
![]()
![]()
![]()
![]()
ce qui justifie ![]() .
.
La propriété est démontrée par récurrence.
Exercice 4
Soit ![]() . Calculer
. Calculer 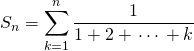 .
.
Corrigé :
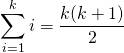
donc
puis
donc
On note dans la suite
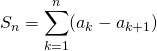
par télescopage
Exercice 5 Formule de Vandermonde
Soit ![]() .
. 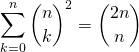 .
.
Corrigé :
Cette démonstration nécessite de savoir faire le produit de deux polynômes.
On utilise ![]()
soit 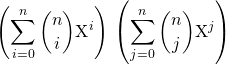
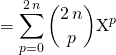 .
.
Puis on égale les coefficients de ![]() :
:
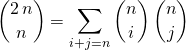
donc
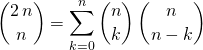
ce qui s’écrit aussi
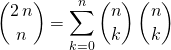
et on a obtenu la relation.
👍 On peut aussi démontrer que si ![]() et
et ![]() et
et ![]() :
:
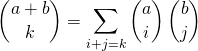
ce qui peut s’écrire
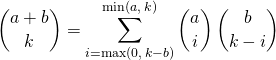
Pour cela on utilise ![]()
et on détermine le coefficient de ![]()
On transforme la somme en choisissant
![]()
ssi ![]()
ce qui donne ![]() .
.
Exercice 6
Soit ![]() . Calculer
. Calculer 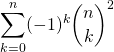
Corrigé :
On utilise ![]()
soit 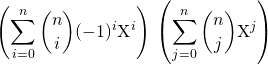
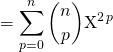
et on calcule le coefficient ![]() de
de ![]()
par le produit des deux polynômes :
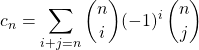
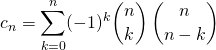
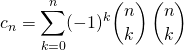
Si ![]() est impair, on en déduit que
est impair, on en déduit que
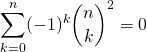
et si ![]() où
où ![]() ,
,
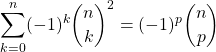 .
.
Exercice 7
Soit ![]() et
et ![]() une famille de réels telle que
une famille de réels telle que
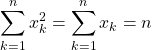 ,
,
alors ![]()
Corrigé :
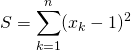
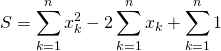
donc ![]() .
.
![]() est nulle et c’est la somme de
est nulle et c’est la somme de ![]() réels positifs ou nuls, donc
réels positifs ou nuls, donc
![]() , soit
, soit ![]() .
.
Exercice 8
Si 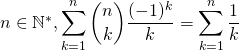
Corrigé :
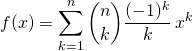
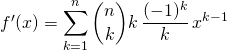
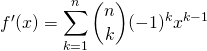
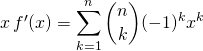
![]() .
.
Si ![]() ,
, ![]()
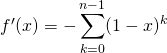
La propriété reste vraie si ![]() car
car ![]() .
.
Puis ![]()
![Rendered by QuickLaTeX.com f(1) = \displaystyle \left [ \sum _{k = 0} ^{n - 1} \frac {(1 - x)^{k + 1} }{k + 1} \right]_0 ^1](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-eb7fb095404c72a2c282c360941b516b_l3.png)
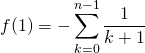
et en posant ![]() ,
,
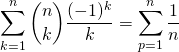 .
.
Exercice 9
Si ![]() , calculer
, calculer 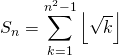
Corrigé :
On écrit une partition de ![]() faisant intervenir les carrés des entiers entre 1 et
faisant intervenir les carrés des entiers entre 1 et ![]()
![Rendered by QuickLaTeX.com [\! [1 \,, \, n ^2 - 1]\! ] = \displaystyle \bigcup _{p = 1} ^{n - 1} [\! [p ^2 \,, \, (p + 1) ^2 - 1]\! ]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0cb391062fbf32b86f7aa94fae63bbf7_l3.png)
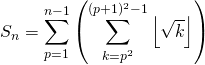
lorsque ![]()
donc
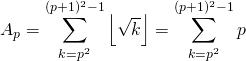
![]()
Donc 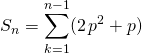
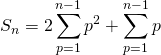
![]()
![]()
![]() .
.
Exercice 10
Calculer si ![]() ,
,
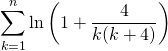 .
.
Corrigé :
![]()
donc ![]()
![]()
On note ![]()
![]()
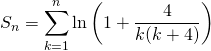
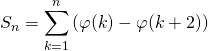
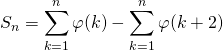
en posant ![]() ,
,
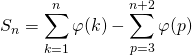
![]()
![]()
![]()
![]()
![]() .
.
![]() \$
\$
4. Calcul de produits
Exercice 1
Si ![]() et
et ![]() , calculer
, calculer
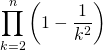 .
.
Corrigé :
![]()
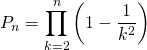
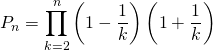
![]() avec
avec
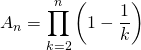
et 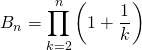 .
.
![]()
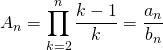
avec 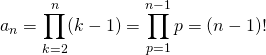
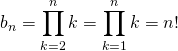
![]() .
.
![]()
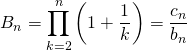
avec 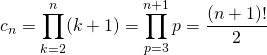
![]() .
.
D’où ![]() .
.
Exercice 2
Exprimer à l’aide factorielles
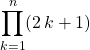 .
.
Corrigé :
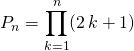 .
.
On utilise ensuite ![]() pour obtenir :
pour obtenir :
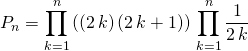
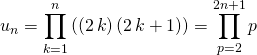
![]()
et 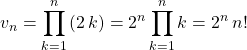
![]() .
.
C’est un calcul que vous allez souvent retrouver.
👍 Il faudra penser à écrire ![]() .
.
Exercice 3
Si ![]() et
et ![]()
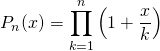 .
.
Question 1
Exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() lorsque
lorsque ![]() .
.
Corrigé :
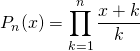
donc 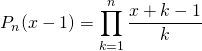 .
.
En posant ![]() ,
,
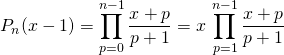
Puis on utilise ![]()
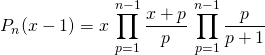
On remarque que 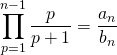
avec 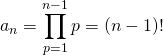
et 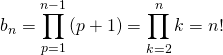
donc 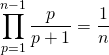
et alors 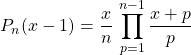
donc 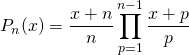
![]() .
.
Question 2
Exprimer si ![]() ,
, ![]() à l’aide de coefficients du binôme.
à l’aide de coefficients du binôme.
Corrigé :
Si ![]() ,
, ![]()
avec 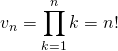
et 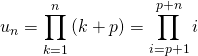
en posant ![]() ,
, ![]() .
.
![]() .
.
Exercice 4
Si ![]() , simplifier
, simplifier 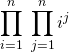 .
.
Corrigé :
Soit 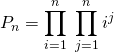 .
.
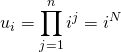
avec 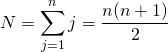
donc ![]() et
et 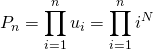
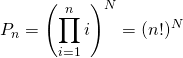
soit ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
5. Sommes doubles
Exercice 1
Si ![]() , calculer
, calculer ![]() .
.
Corrigé :
On note ![]() .
.
![]() Transformation de
Transformation de ![]() : on introduit
: on introduit
![]() ,
, ![]()
et 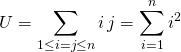 .
.
Par symétrie, ![]() .
.
Comme ![]() est réunion des trois ensembles 2 à 2 disjoints :
est réunion des trois ensembles 2 à 2 disjoints :
![]() ,
,
![]() ,
,
et ![]() ,
,
![]() .
.
![]() Calcul de
Calcul de ![]() .
.
![]()
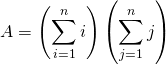
![]() .
.
![]() Conclusion
Conclusion
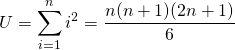 .
.
![]()
![]()
![]()
et ![]()
![]() .
.
Exercice 2
Si ![]() , calculer
, calculer ![]() .
.
Corrigé :
![]()
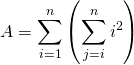
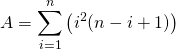
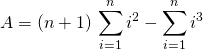
![]()
![]()
![]() .
.
Exercice 3
Si ![]() , calculer
, calculer 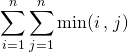 .
.
Corrigé :
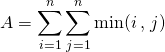 .
.
![]() On traduit d’abord si
On traduit d’abord si ![]()
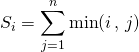
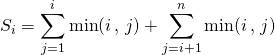
dans la première somme, ![]() et dans la deuxième somme,
et dans la deuxième somme, ![]() ,
,
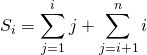
![]()
![]() .
.
![]() Conclusion
Conclusion
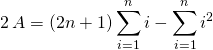
![]()
![]()
et ![]() .
.
Exercice 4
Si ![]() , calculer
, calculer
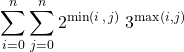 .
.
Corrigé :
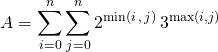
![]() On traduit d’abord si
On traduit d’abord si ![]() ,
,
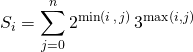
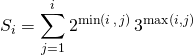
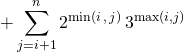
Dans la première somme, ![]() ,
, ![]() et dans la deuxième somme,
et dans la deuxième somme, ![]() ,
, ![]() ,
,
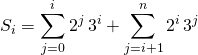
en posant ![]() ,
,
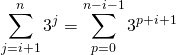
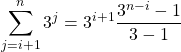
![]()
![]() .
.
![]() Conclusion
Conclusion
![]()
![]()
![]()
![]()
![]() .
.
Exercice 5
Si ![]() et
et ![]() , calculer
, calculer
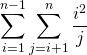 .
.
Corrigé :
![]() Pour intervertir les signes
Pour intervertir les signes ![]() , on écrit la double somme avec un seul signe
, on écrit la double somme avec un seul signe ![]()
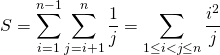
si ![]() est fixé entre
est fixé entre ![]() et
et ![]() ,
, ![]() varie de 1 à
varie de 1 à ![]() :
:
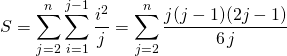
on peut commencer la somme à ![]() car le terme est nul si
car le terme est nul si ![]()
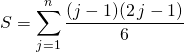 .
.
![]() Fin du calcul
Fin du calcul
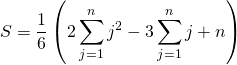
![]()
![]()
![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
6. Formule d’inversion de Pascal
Question 1
Soit ![]() .
.
Montrer que pour tout ![]() ,
, 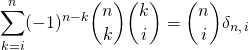
on note ![]() si
si ![]() et 1 si
et 1 si ![]() .
.
Corrigé :
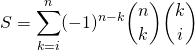
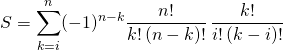
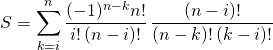
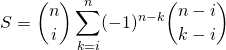
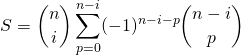
car on obtient
Question 2
Soit ![]() et
et ![]() et
et ![]() deux familles de réels ou complexes.
deux familles de réels ou complexes.
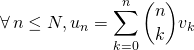
ssi 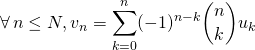 .
.
Corrigé :
![]() Condition nécessaire.
Condition nécessaire.
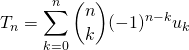
En utilisant la définition de ![]() :
:
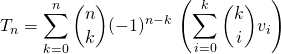
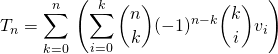
Dans le but d’intervertir les sommes :
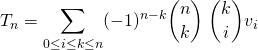
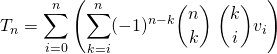
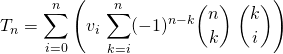
on utilise la première question :
![]()
seul le terme pour ![]() subsiste :
subsiste :
![]() .
.
On a donc établi la condition nécessaire.
![]() Condition suffisante.
Condition suffisante.
On définit pour tout ![]()
![]() et
et ![]()
La première partie donne puisque
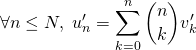
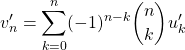
soit après multiplication par ![]()
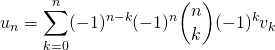
soit 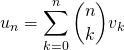 .
.
On a donc prouvé la réciproque.
👍 Cette formule peut être utilisée pour calculer le nombre de surjections ![]() d’un ensemble à
d’un ensemble à ![]() éléments dans un ensemble à
éléments dans un ensemble à ![]() éléments ou le nombre
éléments ou le nombre ![]() de permutations d’un ensemble à
de permutations d’un ensemble à ![]() éléments sans point fixe (telles que pour tout
éléments sans point fixe (telles que pour tout ![]() ,
, ![]() ).
).
Prenez de l’avance sur les cours de maths au programme de Maths Sup avec nos autres cours en ligne et exercices corrigés sur les chapitres suivants :

