Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Dénombrements en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Dénombrements en Maths Sup
Plan :
1. Démontrer qu’un ensemble est fini
2. Utiliser des ensembles finis dans des raisonnements
3. Récapitulatif des résultats
4. Quelle méthode utiliser ?
Retrouvez nos cours particuliers de maths à Paris en cas de lacune ou de perfectionnement de votre niveau en maths sup.
1. Pour démontrer qu’un ensemble est fini
![]() Si
Si ![]() est non vide, démontrer qu’il existe un entier
est non vide, démontrer qu’il existe un entier ![]() et une bijection de
et une bijection de ![]() sur
sur ![]() .
.
Alors ![]() est unique et appelé cardinal de
est unique et appelé cardinal de ![]() et noté
et noté ![]() .
.
![]()
![]() .
.
![]() Démontrer qu’il existe une bijection
Démontrer qu’il existe une bijection ![]() d’un ensemble fini
d’un ensemble fini ![]() sur
sur ![]() .
.
Alors ![]() est fini et
est fini et ![]() .
.
![]() Démontrer que
Démontrer que ![]() est une partie d’un ensemble fini
est une partie d’un ensemble fini ![]() .
.
Alors ![]() .
.
![]() Démontrer que
Démontrer que ![]() est la réunion de deux ensembles finis
est la réunion de deux ensembles finis ![]() et
et ![]()
![]() Si
Si ![]()
![]() .
.
![]() Si
Si ![]() ,
,
![]() .
.
![]() Démontrer que
Démontrer que ![]() avec
avec ![]() et
et ![]() finis :
finis :
![]() .
.
![]() Plus généralement si
Plus généralement si ![]() et si
et si 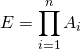 où
où ![]() est fini,
est fini, ![]() est fini et
est fini et 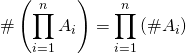 .
.
Exercice
Si ![]() sont trois parties de l’ensemble fini
sont trois parties de l’ensemble fini ![]() , calculer
, calculer ![]() .
.
Démo : On utilise le cardinal d’une réunion de deux ensembles avec ![]() et
et ![]() et
et
![]() .
.
![]()
![]()
![]()
On réutilise la formule donnant le cardinal de la réunion de deux ensembles et la relation :
![]() .
.
![]()
![]()
![]()
et en réordonnant :
![]()
![]()
![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Utiliser des ensembles finis dans des raisonnements
![]() Si
Si ![]() et
et ![]() sont deux ensembles finis de même cardinal et
sont deux ensembles finis de même cardinal et ![]() est une application de
est une application de ![]() dans
dans ![]() ,
,
![]() est bijective ssi
est bijective ssi ![]() est injective ssi
est injective ssi ![]() est surjective.
est surjective.
![]() Si
Si ![]() et
et ![]() sont deux ensembles finis, pour démontrer que
sont deux ensembles finis, pour démontrer que ![]() =
= ![]() , il suffit de prouver une inclusion et que
, il suffit de prouver une inclusion et que ![]() et
et ![]() ont même cardinal.
ont même cardinal.
![]() Si
Si ![]() est une partie de l’ensemble fini
est une partie de l’ensemble fini ![]() , son complémentaire
, son complémentaire ![]() est fini et
est fini et ![]() .
.
3. Récapitulatif des résultats
Dans la suite, ![]() et
et ![]() sont des entiers non nuls et
sont des entiers non nuls et ![]() est un ensemble de cardinal
est un ensemble de cardinal ![]() .
.
![]()
![]() est le nombre
est le nombre
![]() de choix successifs avec remise de
de choix successifs avec remise de ![]() éléments de
éléments de ![]()
![]() de listes avec répétition de
de listes avec répétition de ![]() éléments de
éléments de ![]()
![]() d’applications de
d’applications de ![]() dans
dans ![]() .
.
⚠️ l’ordre des éléments a de l’importance !
![]() Si
Si ![]() ,
, ![]() est le nombre
est le nombre
![]() de choix successifs sans remise de
de choix successifs sans remise de ![]() éléments de
éléments de ![]()
![]() de listes de
de listes de ![]() éléments distincts de
éléments distincts de ![]()
![]() d’applications injectives de
d’applications injectives de ![]() dans
dans ![]() .
.
⚠️ les éléments sont choisis les uns après les autres et les ![]() éléments choisis sont distincts.
éléments choisis sont distincts.
![]() Si
Si ![]() ,
, ![]() est le nombre
est le nombre
![]() de choix simultanés sans remise de
de choix simultanés sans remise de ![]() éléments de
éléments de ![]()
![]() de listes strictement croissantes de
de listes strictement croissantes de ![]() éléments de
éléments de ![]() (h.p. voir dem plus bas )
(h.p. voir dem plus bas )
![]() de parties à
de parties à ![]() éléments de
éléments de ![]() (ou
(ou ![]() combinaisons).
combinaisons).
⚠️ Les éléments sont choisis en même temps. Les ![]() éléments choisis n’ont pas d’ordre.
éléments choisis n’ont pas d’ordre.
Exercice Nombre de listes strictement croissantes de ![]() éléments de
éléments de ![]() .
.
Correction : On suppose ![]() et on note
et on note ![]() l’ensemble
l’ensemble ![]() et
et ![]() l’ensemble des parties de
l’ensemble des parties de ![]() à
à ![]() éléments.
éléments.
L’application ![]()
![]()
est une bijection (toute partie finie peut être rangée d’une unique façon sous forme strictement croissante), donc ![]() .
.
Résultats à savoir démontrer :
si ![]() et
et ![]() ,
,
![]()
![]() .
.
![]()
![]() .
.
Correction :
Soit ![]() l’ensemble des parties de
l’ensemble des parties de ![]() à
à ![]() éléments.
éléments.
![]()
![]() .
.
L’application ![]()
![]()
est une bijection (toute partie finie peut être rangée d’une unique façon sous forme strictement croissante), donc ![]() .
.
![]()
![]()
On écrit ![]() avec
avec ![]()
![]() Si
Si ![]() est un ensemble fini de cardinal
est un ensemble fini de cardinal ![]() ,
, ![]() est fini de cardinal
est fini de cardinal ![]() .
.
En connaître 2 démonstrations :
![]() Première démonstration.
Première démonstration.
Soit ![]() un ensemble fini à
un ensemble fini à ![]() éléments.
éléments.
On écrit 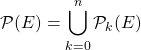
en notant ![]() l’ensemble des parties de
l’ensemble des parties de ![]() à
à ![]() éléments.
éléments.
On introduit ainsi une partition de ![]()
donc 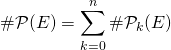
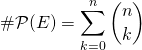
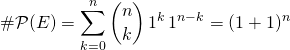
par le binôme de Newton.
![]() Deuxième démonstration.
Deuxième démonstration.
Si ![]() , on note
, on note ![]() .
.
![]()
![]() car
car ![]() .
.
![]() Relation entre
Relation entre ![]() et
et ![]() .
.
Soit ![]() et
et ![]() .
.
On note ![]()
en notant ![]()
et ![]()
![]() et
et ![]() sont disjoints.
sont disjoints.
![]() donc
donc ![]() .
.
![]() est une bijection, donc
est une bijection, donc ![]()
alors ![]()
donne ![]()
![]()
![]() est une suite géométrique de raison 2 et de premier terme
est une suite géométrique de raison 2 et de premier terme ![]()
alors ![]() .
.
![]() Et une troisième démonstration.
Et une troisième démonstration.
On rappelle que l’on note ![]() la fonction indicatrice de l’ensemble
la fonction indicatrice de l’ensemble ![]() .
.
L’application ![]() ,
, ![]() est une bijection, donc
est une bijection, donc
![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
4. Quelle méthode utiliser ?
4.1. Règle du produit
Si l’on doit choisir un premier élément de ![]() façons, un deuxième élément de
façons, un deuxième élément de ![]() façons , … , et le
façons , … , et le ![]() – ième élément de
– ième élément de ![]() façons,
façons,
le nombre de choix possibles est égal à ![]() .
.
c’est en effet le nombre d’éléments de ![]() où
où ![]() est l’ensemble dans lequel on choisit le
est l’ensemble dans lequel on choisit le ![]() -ème élément.
-ème élément.
4.2. Utilisation d’une réunion
Si l’on doit choisir un élément vérifiant une propriété ![]() ou un élément vérifiant une propriété
ou un élément vérifiant une propriété ![]() :
:
On note ![]() (resp
(resp ![]() ) l’ensemble des éléments vérifiant
) l’ensemble des éléments vérifiant ![]() (resp
(resp ![]() ).
).
![]() Dans le cas où il n’y a aucun élément vérifiant les propriétés
Dans le cas où il n’y a aucun élément vérifiant les propriétés ![]() et
et ![]() en même temps :
en même temps :
![]()
car ![]() .
.
![]() Dans le cas où il y a des éléments vérifiant les propriétés
Dans le cas où il y a des éléments vérifiant les propriétés ![]() et
et ![]() en même temps :
en même temps :
![]() .
.
4.3. Utilisation d’une partition
Pour justifier 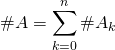 , commencer par prouver que la famille
, commencer par prouver que la famille ![]() est une partition de
est une partition de ![]() (parties non vides, deux à deux disjointes, de réunion égale à
(parties non vides, deux à deux disjointes, de réunion égale à ![]() ).
).
Puis 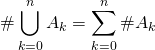 .
.
4.4. « avoir au moins un élément vérifiant une propriété ![]() «
«
![]() Pour dénombrer un problème contenant un « au moins », en général il est plus simple de dénombrer le complémentaire (c’est le cas lorsque le complémentaire se traduit par « sans »).
Pour dénombrer un problème contenant un « au moins », en général il est plus simple de dénombrer le complémentaire (c’est le cas lorsque le complémentaire se traduit par « sans »).
![]() Lorsque le nombre maximum
Lorsque le nombre maximum ![]() d’éléments vérifiant la propriété est faible, on peut envisager de noter
d’éléments vérifiant la propriété est faible, on peut envisager de noter ![]() « avoir
« avoir ![]() éléments vérifiant
éléments vérifiant ![]() » et écrire
» et écrire 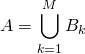 , les ensembles étant deux à deux disjoints,
, les ensembles étant deux à deux disjoints, 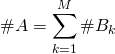
4.5. Calculer ![]() où
où ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() et
et ![]() définie par « avoir au moins un élément vérifiant
définie par « avoir au moins un élément vérifiant ![]() »
»
Utiliser ![]()
![]() .
.
Les deux ensembles étant disjoints :
![]()
et utiliser ![]()
pour répondre à la question.
Les cours en ligne de Maths Sup sont parfaits pour prendre de l’avance en mathématiques en MPSI, PCSI et PTSI. Ainsi, vous pouvez accéder dès maintenant aux chapitres suivants :

