Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Développements limités en Maths Sup MPSI, MP2I, PCSI, PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Maths Sup Développements limités
Plan :
1. Définitions
2. Pour démontrer que ![]() a un développement limité à l’ordre
a un développement limité à l’ordre ![]() en
en ![]()
3. Opérations sur les DL
3.1. Somme de deux DL en 0
3.2. Produit de deux DL en 0.
3.3. Utilisation du DL en ![]() de
de ![]()
3.4. Composition de deux DL en 0
3.5. DL d’un quotient à l’ordre ![]() au voisinage de 0
au voisinage de 0
3.6. Intégration d’un DL
3.7. D.L. et dérivées
3.8. Recherche d’un DL au voisinage de ![]()
3.9. D.L d’une fonction réciproque
4. Les développements limités à connaître
5. Utilisation des DL
5.1. Recherche d’un équivalent
5.2. Caractère local
5.3. Recherche de la limite d’un quotient
5.4. Étude d’une courbe au voisinage de ![]()
5.5. Utilisation des DL dans l’étude des asymptotes obliques.
On note ![]() ou
ou ![]() .
.
Ce chapitre de mathématiques du programme de MPSI, MP2I, PCSI et PTSI est généralement traité au début du second semestre. Il introduit des notions très importantes de maths sup. Ces notions serviront en maths spé pour les concours. Il est primordial de bien savoir calculer les DL et de maitriser les différentes techniques introduites. Si vous en ressentez le besoin, n’hésitez pas à faire appel à un cours particulier de maths à domicile pour maitriser complètement ces fondamentaux.
1. Définitions des DL en MPSI, MP2I, PCSI et PTSI
1.1. Développement limité en ![]() et en
et en ![]()
![]() Soient
Soient ![]() un intervalle et
un intervalle et ![]() un point de
un point de ![]() , ou une borne de
, ou une borne de ![]() et
et ![]() .
.
![]() est une fonction définie sur
est une fonction définie sur ![]() (ou sur
(ou sur ![]() ) à valeurs dans
) à valeurs dans ![]() .
.
![]() On dit que
On dit que ![]() admet un développe- ment limité d’ordre
admet un développe- ment limité d’ordre ![]() en
en ![]() s’il existe
s’il existe ![]() tels que
tels que
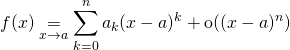
![]() La fonction polynôme
La fonction polynôme 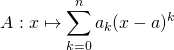 est unique et appelée la partie régulière du DL de
est unique et appelée la partie régulière du DL de ![]() en
en ![]() à l’ordre
à l’ordre ![]() .
.
![]() La fonction
La fonction ![]() admet un développement limité à d’ordre
admet un développement limité à d’ordre ![]() en
en ![]() ssi la fonction
ssi la fonction ![]() admet un développement limité en
admet un développement limité en ![]() d’ordre
d’ordre ![]() et dans ce cas
et dans ce cas
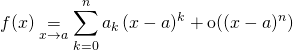
ssi
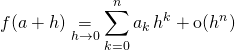 .
.
1.2. Unicité du DL
Il est important de retenir qu’il y a unicité du DL lorsqu’il existe.
Soit ![]() définie dans un intervalle
définie dans un intervalle ![]() centré en
centré en ![]() et admettant un DL d’ordre
et admettant un DL d’ordre ![]() en
en ![]()
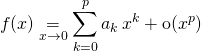 .
.
![]() si
si ![]() est paire, pour tout
est paire, pour tout ![]() tel que
tel que ![]() ,
, ![]() .
.
(la partie régulière du DL ne contient que des puissances paires)
![]() si
si ![]() est paire, pour tout
est paire, pour tout ![]() tel que
tel que ![]() ,
, ![]() .
.
(la partie régulière du DL ne contient que des puissances impaires).
1.3. Troncature
Si ![]() admet un DL d’ordre
admet un DL d’ordre ![]() en
en ![]() :
: 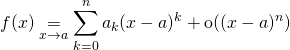 pour tout
pour tout ![]() ,
,
![]() admet un développement limité en
admet un développement limité en ![]() donné par
donné par

On dit qu’il est obtenu par troncature du DL à l’ordre ![]() .
.
Si ![]() admet un développement limité en
admet un développement limité en ![]() , d’ordre
, d’ordre ![]() , elle admet un DL d’ordre
, elle admet un DL d’ordre ![]() donné par
donné par ![]()
![]() si
si ![]() est définie en
est définie en ![]() ,
, ![]()
![]() sinon
sinon ![]() est prolongeable par continuité en
est prolongeable par continuité en ![]() par
par ![]() .
.
1.4. Forme normalisée d’un DL
![]() Si
Si ![]() admet un développement limité d’ordre
admet un développement limité d’ordre ![]() en
en ![]() dont la partie régulière est non nulle, on peut écrire le DL sous la forme dite normalisée :
dont la partie régulière est non nulle, on peut écrire le DL sous la forme dite normalisée :
![]() si
si ![]()
![]()
![]()
En particulier : ![]() .
.
![]() si
si ![]() ,
,
![]()
![]()
En particulier : ![]() .
.
L’entier ![]() est appelé valuation de la partie régulière du DL de
est appelé valuation de la partie régulière du DL de ![]() en
en ![]() .
.
1.5. Développement asymptotique en ![]()
![]() Soit
Soit ![]() définie sur un intervalle de la forme
définie sur un intervalle de la forme ![]() à valeurs dans
à valeurs dans ![]() , si
, si
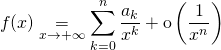 ,
,
On dit que ![]() admet un développement asymptotique à la précision
admet un développement asymptotique à la précision ![]() au voisinage de
au voisinage de ![]() .
.
![]() Soit
Soit ![]() définie sur un intervalle de la forme
définie sur un intervalle de la forme ![]() à valeurs dans
à valeurs dans ![]() , si
, si
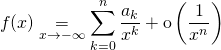 ,
,
On dit que ![]() admet un développement asymptotique à la précision
admet un développement asymptotique à la précision ![]() au voisinage de
au voisinage de ![]() .
.
On peut se ramener au voisinage de ![]() et posant
et posant ![]() soit en utilisant
soit en utilisant ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Pour démontrer que  A UN DÉVELOPPENT LIMITÉ
A UN DÉVELOPPENT LIMITÉ
![]() M1. Par utilisation de la formule de Taylor-Young :
M1. Par utilisation de la formule de Taylor-Young :
Si ![]() est de classe
est de classe ![]() sur un intervalle contenant
sur un intervalle contenant ![]() ,
, ![]() admet un développement limité à l’ordre
admet un développement limité à l’ordre ![]() en
en ![]() donné par
donné par

![]() .
.
Pour cela, il suffit bien sûr que ![]() soit de classe
soit de classe ![]() au voisinage de
au voisinage de ![]() .
.
![]() M2. Montrer que
M2. Montrer que ![]() est une somme de fonctions ayant un DL à l’ordre
est une somme de fonctions ayant un DL à l’ordre ![]() en
en ![]() .
.
![]() M3. Montrer que
M3. Montrer que ![]() où
où ![]() et
et ![]() ont des DL d’ordre
ont des DL d’ordre ![]() en
en ![]() .
.
![]() M4. Si
M4. Si ![]() , montrer que
, montrer que ![]() , où
, où ![]() a un DL d’ordre
a un DL d’ordre ![]() en
en ![]() et
et ![]() a un DL d’ordre
a un DL d’ordre ![]() en
en ![]() avec
avec ![]() de limite nulle en 0.
de limite nulle en 0.
![]() M5. Montrer que
M5. Montrer que ![]() où
où ![]() et
et ![]() ont des DL d’ordre
ont des DL d’ordre ![]() au voisinage de
au voisinage de ![]() , le terme constant du DL de
, le terme constant du DL de ![]() étant non nul.
étant non nul.
![]() M6. Montrer que
M6. Montrer que ![]() est dérivable au voisinage de
est dérivable au voisinage de ![]() et que
et que ![]() a un DL d’ordre
a un DL d’ordre ![]() en
en ![]() .
.
![]() M7. Si l’on connaît le DL de
M7. Si l’on connaît le DL de ![]() en
en ![]() à l’ordre
à l’ordre ![]() , le DL de
, le DL de ![]() à l’ordre
à l’ordre ![]() est obtenu par troncature.
est obtenu par troncature.
![]() M8. Toute fonction polynôme
M8. Toute fonction polynôme ![]() de degré inférieur ou égal à
de degré inférieur ou égal à ![]() admet un DL d’ordre
admet un DL d’ordre ![]() au voisinage de
au voisinage de ![]() dont la partie régulière est égale à
dont la partie régulière est égale à ![]() .
.
Pour que ![]() admette un DL en
admette un DL en ![]() , il est nécessaire que
, il est nécessaire que ![]() ait une limite finie en
ait une limite finie en ![]() . Si
. Si ![]() est définie en
est définie en ![]() , il est nécessaire que
, il est nécessaire que ![]() soit continue en
soit continue en ![]() .
.
Si une fonction est paire (resp. impaire) et a un DL d’ordre ![]() en
en ![]() , son DL ne contient que des puissances paires (resp impaires).
, son DL ne contient que des puissances paires (resp impaires).
Mais un DL ne contenant que des puissances paires (resp. impaires) n’est pas nécessairement le DL d’une fonction paire (resp impaire).
![]() M9. Pour obtenir un DL d’ordre
M9. Pour obtenir un DL d’ordre ![]() de
de ![]() au voisinage de
au voisinage de ![]() (resp. de
(resp. de ![]() ), chercher un DL d’ordre
), chercher un DL d’ordre ![]() au voisnage de
au voisnage de ![]() (resp
(resp ![]() ) de
) de ![]() .
.
3. Opérations sur les DL
Il est conseillé de se ramener au voisinage de ![]() en posant
en posant ![]() lorsque
lorsque ![]() .
.
Toutes les opérations doivent se faire avec des DL de même ordre.
3.1. Somme de deux DL en 0
On écrit les deux DL à l’ordre ![]() . On additionne les parties régulières.
. On additionne les parties régulières.
3.2. Produit de deux DL en 0.
On écrit les deux DL à l’ordre ![]() . On fait le produit des parties régulières en ne conservant que les termes de degré inférieur ou égal à
. On fait le produit des parties régulières en ne conservant que les termes de degré inférieur ou égal à ![]() .
.
Si ![]()
et ![]() ,
,
En notant
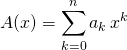 et
et  ,
,
alors ![]()
où 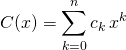 avec
avec ![Rendered by QuickLaTeX.com \quad \forall\, k \in [\![0 , \, n]\!], \, c_k = \displaystyle \sum _{i = 0} ^k a_i \, b_{k - i}\,](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d12aa71937766669248b438e183eb4db_l3.png) .
.
Si l’on élève le DLde ![]() à l’ordre
à l’ordre ![]() au carré, on obtient le DL de
au carré, on obtient le DL de ![]() à l’ordre
à l’ordre ![]() (et non à l’ordre
(et non à l’ordre ![]() ).
).
Ne jamais faire le produit d’un DL en ![]() par une expression contenant des puissances négatives de
par une expression contenant des puissances négatives de ![]() .
.
3.3. Utilisation du DL de ![]()
On rappelle que si ![]()
![]()

![]()
Même si la formule est utilisable pour ![]() , il est indispensable de connaître par coeur :
, il est indispensable de connaître par coeur :
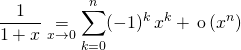 .
.
Lorsque ![]() , il suffit d’utiliser le binôme de Newton (tronqué si
, il suffit d’utiliser le binôme de Newton (tronqué si ![]() ) et d’écrire
) et d’écrire
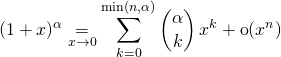
Exemple :
Trouver le développement limité de ![]() à l’ordre 4 en
à l’ordre 4 en ![]() .
.
Correction : On utilise la formule pour ![]()
![]()

et on évalue ![]() pour
pour ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
Exemple 2 :
Trouver le développement limite de ![]() à l’ordre
à l’ordre ![]() en
en ![]() .
.
En exprimer les coefficients à l’aide de coefficients binomiaux.
Correction :
On utilise la formule
![]()

Pour ![]() et on simplifie la valeur de
et on simplifie la valeur de ![]()
![]()
![]() .
.
On calcule la valeur de ![]()
en multipliant et divisant par ![]()
![]()
![]()
![]()
donc ![]()
![]() .
.
Cette formule donne ![]() si
si ![]() , on peut donc écrire :
, on peut donc écrire :
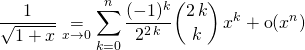
Bien sûr si l’on demande le développement limité à un ordre simple, on effectue uniquement les calculs indis- pensables et on obtient par exemple :
![]()
![]()
3.4. Composition de deux DL en 0
Avant de calculer le DL de ![]() au voisinage de
au voisinage de ![]() , lorsque l’on connaît les DL de
, lorsque l’on connaît les DL de ![]() et
et ![]() à l’ordre
à l’ordre ![]() au voisinage de 0, bien vérifier que
au voisinage de 0, bien vérifier que ![]() tend vers 0 en 0 (c’est à dire que le terme constant du DL de
tend vers 0 en 0 (c’est à dire que le terme constant du DL de ![]() est nul).
est nul).
Méthode pratique
![]() a) on écrit le DL de
a) on écrit le DL de ![]() quand
quand ![]() tend vers
tend vers ![]() à l’ordre
à l’ordre ![]()
![]() b) on écrit le DL de
b) on écrit le DL de ![]() quand
quand ![]() tend vers 0 à l’ordre
tend vers 0 à l’ordre ![]() , en vérifiant que la partie régulière
, en vérifiant que la partie régulière ![]() de ce DL ne contient pas de terme constant
de ce DL ne contient pas de terme constant
![]() c) dans la partie régulière
c) dans la partie régulière ![]() du DL de
du DL de ![]() , on remplace
, on remplace ![]() par
par ![]() . On élève
. On élève ![]() ) aux différentes puissances, en ne conservant que les termes de degré inférieur ou égal à
) aux différentes puissances, en ne conservant que les termes de degré inférieur ou égal à ![]() .
.
![]() d) on remplace
d) on remplace ![]() par
par ![]() .
.
Exemple 1 :
Développement limité à l’ordre 5 en ![]() de
de ![]() .
.
Correction :
On rappelle les DL utilisés ici :
![]()
![]()
![]()
Il n’y a pas de problème de composition puisque ![]() tend vers
tend vers ![]() en
en ![]() .
.
On pose donc ![]() .
.
Vous préférerez peut être faire les calculs suivants à part (on multiplie chaque ligne par ![]() en ne conservant que les monômes de degré inférieur ou égal à
en ne conservant que les monômes de degré inférieur ou égal à ![]() ) :
) :
![]()
![]()
![]()
![]()
Pour obtenir
![]()
![]()
![]()
Puis on réordonne suivant les puissances croissantes de ![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
Dans le cas où ![]() , suivant la situation :
, suivant la situation :
![]() On utilise les propriétés de
On utilise les propriétés de ![]() pour exprimer
pour exprimer ![]() en fonction de
en fonction de ![]() (
(![]() ) dont on peut écrire le développement limité en suivant la méthode décrite ci- dessus.
) dont on peut écrire le développement limité en suivant la méthode décrite ci- dessus.
![]() Sinon il faut écrire le développement limité de
Sinon il faut écrire le développement limité de ![]() à l’ordre
à l’ordre ![]() en
en ![]() sous la forme
sous la forme

Et remplacer ![]() par
par ![]() .
.
Exemple 2
DL à l’ordre 5 en ![]() de
de ![]() .
.
Correction :
Avant de faire les calculs, on rappelle que la fonction ![]() étant paire, si l’on connaît le DL de
étant paire, si l’on connaît le DL de ![]() à l’ordre
à l’ordre ![]() en
en ![]() , on le connaît à l’ordre 5.
, on le connaît à l’ordre 5.
On rappelle les DL utilisés ici :
![]()
![]() .
.
Puis on fait attention au fait que ![]() admet
admet ![]() pour limite en
pour limite en ![]() , on écrit donc
, on écrit donc
![]()
avec
![]()
Puis comme le DL de ![]() commence par
commence par ![]() , seuls les calculs de
, seuls les calculs de ![]() ,
, ![]() sont utiles pour trouver le DL de
sont utiles pour trouver le DL de ![]() .
.
Avec ces remarques, les calculs sont simplifiés :
![]()
![]()
Ce qui donne le DL à l’ordre 4 :
![]()
![]()
Soit
![]()
On termine en utilisant la remarque indiquant que le DL à l’ordre 4 d’une fonction paire donne le DL à l’ordre 5 et
![]()
Exemple 3
DL à l’ordre 2 en ![]() de
de ![]() .
.
Correction : On sait que ![]() .
.
On écrit le DL de ![]() en
en ![]() à l’ordre 2 à l’aide de la formule de Taylor-Young.
à l’ordre 2 à l’aide de la formule de Taylor-Young.
![]() ,
, ![]()
![]() ,
, ![]() .
.
![]()
![]()
et on utilise ![]()
donc ![]()
![]()
![]() .
.
3.5. DL d’un quotient à l’ordre ![]() au voisinage de 0
au voisinage de 0
Soit à calculer le DL de ![]() à l’ordre
à l’ordre ![]() .
.
![]() 1 er cas : le DL de
1 er cas : le DL de ![]() a un terme constant non nul.
a un terme constant non nul.
On écrit les DL de ![]() et
et ![]() à l’ordre
à l’ordre ![]() en
en ![]() :
: ![]() et
et ![]() .
.
En divisant par le terme constant ![]() non nul de
non nul de ![]() les quantités
les quantités ![]() et
et ![]() , on se ramène à une expression de la forme
, on se ramène à une expression de la forme ![]() ,
,
La fonction ![]() admettant
admettant ![]() pour limite en
pour limite en ![]() . On utilise le DL de
. On utilise le DL de ![]() pour obtenir celui de
pour obtenir celui de ![]() puis on fait un produit de 2 développements limités.
puis on fait un produit de 2 développements limités.
Exemple 1 :
DL de ![]() en
en ![]() à l’ordre 3.
à l’ordre 3.
Correction :
![]() en
en ![]() à l’ordre 2.
à l’ordre 2.
![]() Comme le dénominateur admet
Comme le dénominateur admet ![]() pour limite en
pour limite en ![]() , on écrit les développements limités du numérateur
, on écrit les développements limités du numérateur
![]() et du dénominateur
et du dénominateur ![]() à l’ordre 2.
à l’ordre 2.
![]()
![]()
![]()
![]()
avec ![]()
![]()
![]()
et en factorisant ![]()
![]()
![]() En utilisant
En utilisant ![]()
pour ![]()
![]()
![]() .
.
![]() Il reste à faire un produit de deux DL à l’ordre 2 :
Il reste à faire un produit de deux DL à l’ordre 2 :
![]()
![]()
![]() .
.
![]() 2 ème cas : le DL de
2 ème cas : le DL de ![]() a un terme constant nul et
a un terme constant nul et ![]() (la valuation de la partie régulière du DL de
(la valuation de la partie régulière du DL de ![]() est égale à
est égale à ![]() ).
).
![]() si la valuation de
si la valuation de ![]() est supérieure ou égale à
est supérieure ou égale à ![]() , on écrit les DL de
, on écrit les DL de ![]() et
et ![]() à l’ordre
à l’ordre ![]() . On simplifie par
. On simplifie par ![]() et on se ramène au premier cas.
et on se ramène au premier cas.
![]() si la valuation
si la valuation ![]() de
de ![]() vérifie
vérifie ![]() , on introduit
, on introduit ![]() .
.
Les valuations des nouvelles parties régulières ![]() et
et ![]() sont alors égales à
sont alors égales à ![]() , ce qui permet d’appliquer la méthode décrite dans le deuxième cas à
, ce qui permet d’appliquer la méthode décrite dans le deuxième cas à ![]() .
.
Il est alors indispensable de réfléchir aux ordres des différents DL si l’on veut une expression de ![]() en
en ![]()
Il faut écrire celui de ![]() à l’ordre
à l’ordre ![]() (pour simplifier à la fin par
(pour simplifier à la fin par ![]() ).
).
Les valuations des parties régulières du numérateur et du dénominateur étant égales à ![]() , il faut écrire ces développements limites de
, il faut écrire ces développements limites de ![]() et de
et de ![]() à l’ordre
à l’ordre ![]() , les simplifier par
, les simplifier par ![]() , utiliser la méthode décrite dans le 1er cas au quotient de deux DL à l’ordre
, utiliser la méthode décrite dans le 1er cas au quotient de deux DL à l’ordre ![]() dont la valuation du dénominateur est nulle et ainsi obtenir le DL de
dont la valuation du dénominateur est nulle et ainsi obtenir le DL de ![]() à l’ordre
à l’ordre ![]() comme souhaité.
comme souhaité.
Si l’on a écrit le développement limité de ![]() sous la forme :
sous la forme :
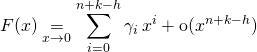
on obtient
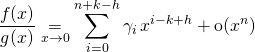 .
.
On remarquera que la partie 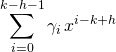 est formée de termes élevés à une puissance strictement négative.
est formée de termes élevés à une puissance strictement négative.
exemple 2
Développement limité à l’ordre 4 de ![]() .
.
Correction :
La valuation du DL de ![]() en
en ![]() étant égale à 1, il faut diviser par
étant égale à 1, il faut diviser par ![]() , donc écrire le DL de
, donc écrire le DL de ![]() à l’ordre 5
à l’ordre 5
![]()
![]() .
.
En utilisant ![]()
avec ![]()
![]() .
.
Les termes ![]() et
et ![]() ne contiennent pas de termes de degré inférieur ou égal à 4,
ne contiennent pas de termes de degré inférieur ou égal à 4,
donc ![]()
![]() .
.
3.6. Intégration
Si au voisinage de ![]() , la fonction continue
, la fonction continue ![]() vérifie :
vérifie : 
une primitive ![]() de
de ![]() admet pour DL au voisinage de
admet pour DL au voisinage de ![]() :
:
![]()
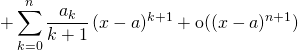
Il n’y a aucune difficulté si l’on n’oublie pas ![]() .
.
Il est bon de savoir que le DL de ![]() se calcule plus simplement en utilisant le DL de
se calcule plus simplement en utilisant le DL de ![]() qu’en faisant une composition de DL .
qu’en faisant une composition de DL .
C’est en utilisant cette méthode que l’on retrouve facilement les DL de ![]() à l’ordre
à l’ordre ![]() ou de
ou de ![]() à l’ordre
à l’ordre ![]() en
en ![]()
exemple 1
Déterminer le développement limité en ![]() à l’ordre
à l’ordre ![]() de
de ![]()
Correction :
![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
On a vu en 3.3 que

![]()
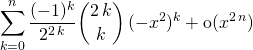
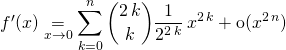
Par intégration du DL sachant que ![]() ,
,
![]()
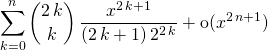 .
.
exemple 2
Retrouver le DL à l’ordre 2 en ![]() de
de ![]() .
.
Correction :
![]()
![]()
On effectue le produit de deux DL à l’ordre 1 :
![]()
![]()
et comme ![]() ,
,
![]()
3.7. D.L. et dérivées
![]() M1.
M1. ![]() est définie dans un voisinage de
est définie dans un voisinage de ![]() et a un DL d’ordre
et a un DL d’ordre ![]() en
en ![]() tronqué à l’ordre 1 sous la forme :
tronqué à l’ordre 1 sous la forme :
![]()
alors ![]() et
et ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
Si ![]() n’était pas définie en
n’était pas définie en ![]() , on la prolonge par continuité en
, on la prolonge par continuité en ![]() en posant
en posant ![]() .
.
![]() M2. Si
M2. Si ![]() est de classe
est de classe ![]() au voisina- ge de
au voisina- ge de ![]() ,
, ![]() a un DL d’ordre
a un DL d’ordre ![]() en
en ![]() donné par la formule de Taylor-Young.
donné par la formule de Taylor-Young.
Conséquence : si ![]() est de classe
est de classe ![]() ;
; ![]() a un DL en
a un DL en ![]() à l’ordre
à l’ordre ![]() pour tout
pour tout ![]() .
.
![]() M3.Si
M3.Si ![]() est
est ![]() fois dérivable en
fois dérivable en ![]() et si l’on a obtenu son DL à l’ordre
et si l’on a obtenu son DL à l’ordre ![]() :
:
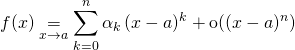
![]() alors
alors ![]() .
.
![]()
![]() admet un DL d’ordre
admet un DL d’ordre ![]() en
en ![]() donné par :
donné par :
![]()
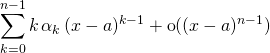
![]() M4. Si
M4. Si ![]() est une fonction dérivable sur un intervalle
est une fonction dérivable sur un intervalle ![]() contenant
contenant ![]() et si
et si ![]() et
et ![]() admettent des DL d’ordre
admettent des DL d’ordre ![]() et
et ![]() respectivement au voisinage de
respectivement au voisinage de ![]() , alors la partie régulière du DL à l’ordre
, alors la partie régulière du DL à l’ordre ![]() en
en ![]() de
de
![]() est la dérivée de la partie régulière du DL à l’ordre
est la dérivée de la partie régulière du DL à l’ordre ![]() en
en ![]() de
de ![]()
![]() M5. Si
M5. Si ![]() a un DL d’ordre
a un DL d’ordre ![]() en
en ![]() et si
et si ![]() est dérivable au voisinage de
est dérivable au voisinage de ![]() , on ne peut pas dériver le DL de
, on ne peut pas dériver le DL de ![]() sauf si l’on sait que
sauf si l’on sait que ![]() vérifie les conditions de Taylor Young (cf M3.) ou la condition du M4.
vérifie les conditions de Taylor Young (cf M3.) ou la condition du M4.
![]() Il existe des fonctions ayant un DL d’ordre
Il existe des fonctions ayant un DL d’ordre ![]() en
en ![]() et qui ne sont pas
et qui ne sont pas ![]() fois dérivables en
fois dérivables en ![]() si
si ![]() .
.
exemple : ![]() et
et ![]() ,
, ![]() , mais
, mais ![]() n’existe pas.
n’existe pas.
Si ![]() et si
et si ![]() a un DL d’ordre
a un DL d’ordre ![]() en
en ![]() , on ne peut pas conclure que
, on ne peut pas conclure que ![]() est
est ![]() fois dérivable en
fois dérivable en ![]() , ni que
, ni que ![]() est de classe
est de classe ![]() au voisinage de
au voisinage de ![]() .
.
Démo :
![]() Soit
Soit ![]() ,
, ![]() ,
, ![]() , ce qui permet d’écrire
, ce qui permet d’écrire ![]() , donc
, donc ![]() a un DL d’ordre 2 en
a un DL d’ordre 2 en ![]() .
.
![]()
![]() ayant un DL à l’ordre 1 en
ayant un DL à l’ordre 1 en ![]() ,
, ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
Soit ![]()
![]() .
.
![]() En utilisant
En utilisant ![]() , la suite
, la suite ![]() converge vers
converge vers ![]() .
.
![]() , la suite
, la suite ![]() converge vers
converge vers ![]() .
.
![]()
![]() , la suite
, la suite ![]() converge vers
converge vers ![]() .
.
![]() , la suite
, la suite ![]() converge pas vers
converge pas vers ![]() ,
,
La fonction ![]() n’admet pas de limite en
n’admet pas de limite en ![]() , donc
, donc ![]() n’est pas dérivable en
n’est pas dérivable en ![]() .
.
3.8. Recherche d’un DL au voisinage de ![]()
![]() lorsque
lorsque ![]() , par utilisation de la formule de Taylor Young, à condition que la fonction
, par utilisation de la formule de Taylor Young, à condition que la fonction ![]() soit de classe
soit de classe ![]() au voisinage de
au voisinage de ![]() .
.
![]() ou par changement d’inconnue (en posant
ou par changement d’inconnue (en posant ![]() si
si ![]() ou
ou ![]() si
si ![]() ), à condition d’obtenir un DL calculable en 0.
), à condition d’obtenir un DL calculable en 0.
quand les calculs sont terminés, ne pas développer les puissances de ![]() obtenues.
obtenues.
3.9. D.L d’une fonction réciproque
rappels : si ![]() est une fonction continue sur l’intervalle
est une fonction continue sur l’intervalle ![]() et strictement monoto- ne,
et strictement monoto- ne, ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
Si l’on suppose de plus que ![]() est de classe
est de classe ![]() sur
sur ![]() et que pour tout
et que pour tout ![]() de
de ![]() ,
, ![]() , la fonction réciproque
, la fonction réciproque ![]() de
de ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Conséquence : Si les hypothèses ci-dessus sont vérifiées et si ![]() est un intervalle contenant
est un intervalle contenant ![]() ,
, ![]() est de classe
est de classe ![]() au voisinage de
au voisinage de ![]() donc admet un développement limité à l’ordre
donc admet un développement limité à l’ordre ![]() au voisinage de
au voisinage de ![]() .
.
On écrit le DL de ![]() en
en ![]() à l’ordre
à l’ordre ![]() et celui de
et celui de ![]() en
en ![]() sous la forme
sous la forme
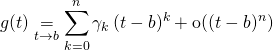
et en écrivant que ![]() et en calculant le DL de cette égalité à l’ordre
et en calculant le DL de cette égalité à l’ordre ![]() en
en ![]() , par unicité du DL de la fonction
, par unicité du DL de la fonction ![]() en
en ![]() , on obtient un système d’équations permettant de calculer les
, on obtient un système d’équations permettant de calculer les ![]() .
.
exemple :
Existence de la fonction réciproque de ![]() et détermination du DL de la fonction réciproque à l’ordre
et détermination du DL de la fonction réciproque à l’ordre ![]() en
en ![]() .
.
Correction :
![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]()
![]() admet
admet ![]() pour limite à droite en
pour limite à droite en ![]() et
et ![]() pour limite en
pour limite en ![]() . Donc
. Donc ![]() définit une bijection de
définit une bijection de
![]() sur
sur ![]() et sa fonction réciproque
et sa fonction réciproque ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
De plus ![]() donc
donc ![]() admet un développement limité à l’ordre
admet un développement limité à l’ordre ![]() en
en ![]() donné par
donné par ![]() .
.
Et ![]() .
.
On peut effectuer la composition des DL pour trouver le DL de ![]() en
en ![]()
![]()
![]()
![]()
![]()
or ![]() , donc par unicité du DL, on obtient les CNS
, donc par unicité du DL, on obtient les CNS
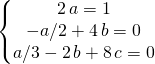
ssi ![]() et
et ![]()
donc ![]() .
.
4. Les développements limités classiques à connaître
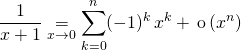
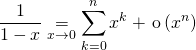
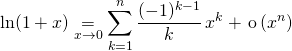
qui permet de trouver
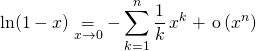
![]()
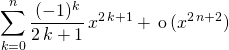
![]()
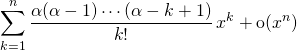
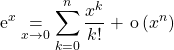
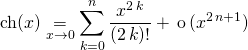
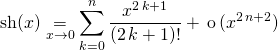

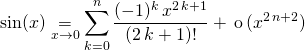
![]()
et ceux à savoir retrouver
![]()
![]()
![]()
![]()
![]()
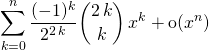 .
.
5. Utilisation des développements limités en MPSI, PTSI, MP2I et PCSI
5.1. Trouver un équivalent
On suppose que l’on a obtenu le DL de ![]() à l’ordre
à l’ordre ![]() au voisinage de
au voisinage de ![]() , de partie régulière non nulle :
, de partie régulière non nulle :
![]() si
si ![]() ,
,
![]()
![]() si
si ![]() ,
,
![]() .
.
On note ![]() le plus petit entier tel que
le plus petit entier tel que ![]() soit non nul, alors
soit non nul, alors
![]()
![]() si
si ![]()
![]()
![]() si
si ![]() .
.
Important : on ne conserve qu’un seul terme du DL lorsque l’on écrit un équivalent.
En général, il faut utiliser un DL quand on cherche un équivalent de ![]() , formée d’une somme ou d’une différence.
, formée d’une somme ou d’une différence.
5.2. Caractère local
Un DL ne donne des renseignements qu’au voisinage du point considéré.
Il ne permet pas de donner le signe de ![]() pour tout
pour tout ![]() , mais si l’on peut en déduire qu’il existe
, mais si l’on peut en déduire qu’il existe
![]() et
et ![]() tels que
tels que ![]() , il permet de dire que, pour
, il permet de dire que, pour ![]() assez petit,
assez petit, ![]() et
et ![]() sont de même signe.
sont de même signe.
5.3. Recherche de la limite d’un quotient
Dans le cas d’une forme indéterminée 0/0, on cherche un équivalent du dénominateur et on écrit le DL du numérateur au même ordre.
Dans le cas d’une différence de quotients, réduire auparavant au même dénominateur.
5.4. Étude d’une courbe au voisinage de ![]()
Dans la plupart des cas, il suffit d’avoir le DL de ![]() à l’ordre 2 en
à l’ordre 2 en ![]() (à l’ordre 3 si
(à l’ordre 3 si ![]() est impaire et si
est impaire et si ![]() ).
).
Si l’on obtient
![]()
![]()
![]() Si nécessaire, on prolonge
Si nécessaire, on prolonge ![]() par continuité en
par continuité en ![]() , en posant
, en posant ![]() . Alors
. Alors ![]() est dérivable en
est dérivable en
![]() et
et ![]() .
.
![]() Une équation de la tangente en
Une équation de la tangente en ![]() est
est ![]() .
.
Pour étudier la position par rapport à la tangente, on étudie le signe de ![]() :
:
![]() si
si ![]() , le signe de
, le signe de ![]() est le signe de
est le signe de ![]() donc le signe de
donc le signe de ![]() pour
pour ![]() assez petit.
assez petit.
![]() si
si ![]() , il faut refaire le DL de
, il faut refaire le DL de ![]() à un ordre plus élevé et dans le cas où l’on a obtenu
à un ordre plus élevé et dans le cas où l’on a obtenu
![]() ,
,
![]() est alors du signe de
est alors du signe de ![]() pour
pour ![]() assez petit.
assez petit.
Lorsque ![]() est impair,
est impair, ![]() change de signe en
change de signe en ![]() : la courbe traverse sa tangente en
: la courbe traverse sa tangente en ![]() , on dit que le graphe
, on dit que le graphe ![]() admet un point d’inflexion en
admet un point d’inflexion en ![]() .
.
![]() Étude des points critiques : (points tels que
Étude des points critiques : (points tels que ![]() ).
).
Dans le cas où l’on peut trouver ![]() et
et ![]() tels que
tels que ![]()
![]() si
si ![]() est pair,
est pair, ![]() admet un maximum local en
admet un maximum local en ![]() si
si ![]() et un minimum local si
et un minimum local si ![]()
![]() si
si ![]() est impair,
est impair, ![]() change de signe en
change de signe en ![]() , la courbe traverse sa tangente en
, la courbe traverse sa tangente en ![]() , on a un point d’inflexion à tangente horizontale.
, on a un point d’inflexion à tangente horizontale.
(on trouve ![]() et
et ![]() en utilisant un DL en
en utilisant un DL en ![]() de
de ![]() ).
).
5.5. Utilisation des DL dans l’étude des asymptotes obliques
On pose ![]() et on calcule le DL de
et on calcule le DL de ![]() à l’ordre
à l’ordre ![]() quand
quand ![]() tend vers 0.
tend vers 0.
On obtient une expression de la forme
![]() soit
soit ![]() .
.
La courbe représentative ![]() de
de ![]() admet une asymptote
admet une asymptote ![]() d’équation
d’équation ![]() .
.
Pour ![]() , le signe de
, le signe de ![]() est celui de
est celui de ![]() et il donne la position de la courbe par rapport à l’asymptote.
et il donne la position de la courbe par rapport à l’asymptote.
Dans le cas ![]() , il faut refaire le DL de
, il faut refaire le DL de ![]() à un ordre plus élevé.
à un ordre plus élevé.
Exemple
Étude des branches infinies de ![]() où
où ![]() .
.
Correction :
![]() où
où ![]() .
.
On note ![]() ,
, ![]() .
.
Pour éviter un calcul supplémentaire qui serait dû à une valeur de ![]() annulant le coefficient de
annulant le coefficient de ![]() , on prend la précaution de calculer le développement limité à l’ordre 3 et non 2.
, on prend la précaution de calculer le développement limité à l’ordre 3 et non 2.
![]()
![]()
![]()
![]()
donc
![]()
![]()
ce qui donne ![]()
La droite ![]() d’équation
d’équation ![]() est asymptote à la courbe
est asymptote à la courbe ![]() .
.
On étudie le signe de ![]() au voisinage de
au voisinage de ![]() .
.
![]() si
si ![]() ,
, ![]()
au voisinage de ![]() ,
, ![]() est du signe de
est du signe de ![]()
![]() si
si ![]() , la courbe est au dessus de l’asymptote si
, la courbe est au dessus de l’asymptote si ![]() et en dessous si
et en dessous si ![]()
![]() si
si ![]() , la courbe est au dessus de l’asymptote si
, la courbe est au dessus de l’asymptote si ![]() et en dessous si
et en dessous si ![]() .
.
![]() si
si ![]() ,
,
![]()
![]() donc est négatif au voisinage de l’infini.
donc est négatif au voisinage de l’infini.
La courbe est située sous l’asymptote.
Les cours de maths dispensés en prépa ne sont évidemment pas suffisants pour espérer avoir une bonne moyenne. Par conséquent, ces cours en ligne au programme de Maths pour les Maths Sup vous offrent la possibilité de compléter chez vous, les enseignements reçus en cours. Tous les chapitres de maths de MPSI, PTSI et PCSI sont disponibles, dont les chapitres suivants :

