Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours sur les espaces vectoriels en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Bénéficiez de cours en ligne sur le chapitre des espaces vectoriels au programme de maths sup en maths. Un cours de maths qui viendra compléter les cours dispensés par les professeurs de prépa mais aussi les cours particuliers de maths tout au long de l’année.
*Dans tout le chapitre, ![]() désigne le corps des réels ou des complexes.*
désigne le corps des réels ou des complexes.*
A. Espaces vectoriels de dimension finie en Maths Sup
1. Définition des espaces vectoriels de dimension fini en maths sup
D1 : Un ![]() -espace vectoriel
-espace vectoriel ![]() est de dimension finie lorsqu’il admet une famille génératrice finie.
est de dimension finie lorsqu’il admet une famille génératrice finie.
Théorème de la base extraite :
Si ![]() est un espace vectoriel de dimension finie distinct de
est un espace vectoriel de dimension finie distinct de ![]() , de toute famille génératrice finie, on peut extraire une base de
, de toute famille génératrice finie, on peut extraire une base de ![]() .
.
Théorème de la base incomplète :
Soit ![]() un espace vectoriel de dimension finie. Toute famille libre de
un espace vectoriel de dimension finie. Toute famille libre de ![]() peut être complétée en une base de
peut être complétée en une base de ![]() .
.
2. Dimension des espaces vectoriels
T1 : Dans un espace vectoriel engendré par une famille de ![]() vecteurs, toute famille de
vecteurs, toute famille de ![]() vecteurs est liée.
vecteurs est liée.
T2 : Si ![]() est un espace vectoriel de dimension finie distinct de
est un espace vectoriel de dimension finie distinct de ![]() , toutes les bases de
, toutes les bases de ![]() ont même cardinal, que l’on appelle dimension de
ont même cardinal, que l’on appelle dimension de ![]() et que l’on note
et que l’on note ![]() .
.
On pose par convention ![]() .
.
3. Produit d’un nombre fini d’espaces vectoriels de dimension finie
Soit ![]() et
et ![]() .
.
On suppose que pour tout ![]() ,
,
![]() est un
est un ![]() -espace vectoriel de dimension finie.
-espace vectoriel de dimension finie. ![]() est un
est un ![]() -espace vectoriel de dimension finie et
-espace vectoriel de dimension finie et
![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
B. Propriétés des espaces vectoriels de dimension finie en Maths Sup
1. Caractérisation d’une base d’un espace vectoriel
P1 : Soit ![]() un
un ![]() -espace vectoriel de dimension
-espace vectoriel de dimension ![]() et
et ![]() une famille de
une famille de ![]() vecteurs de
vecteurs de ![]() .
.
![]() est une base de
est une base de ![]()
![]()
![]() est une famille libre de
est une famille libre de ![]()
![]()
![]() est une famille génératrice de
est une famille génératrice de ![]() .
.
2. Sous-espace vectoriel d’un espace vectoriel de dimension finie
P2 : Si ![]() est un
est un ![]() -espace vectoriel de dimension finie et
-espace vectoriel de dimension finie et ![]() est un s.e.v. de
est un s.e.v. de ![]() ,
,
![]()
![]() est de dimension finie et
est de dimension finie et ![]()
![]()
![]() ssi
ssi ![]()
P3 : Formule de Grassmann
Soient ![]() et
et ![]() deux sous-espaces vectoriels de dimension finie du
deux sous-espaces vectoriels de dimension finie du ![]() -espace vectoriel
-espace vectoriel ![]() ,
, ![]() est de dimension finie et
est de dimension finie et
![]()
![]()
3. Rang d’une famille de vecteurs en Maths Sup
D : Le rang de la famille de vecteurs ![]() du
du ![]() -espace vectoriel
-espace vectoriel ![]() est égal à
est égal à ![]() .
.
On le note ![]() .
.
P4 : Le rang de la famille ![]() est inchangé
est inchangé
![]() si l’on permute les vecteurs,
si l’on permute les vecteurs,
![]() si l’on multiplie un vecteur par un scalaire non nul
si l’on multiplie un vecteur par un scalaire non nul
![]() si l’on ajoute à l’un des vecteurs une combinaison linéaire des autres vecteurs.
si l’on ajoute à l’un des vecteurs une combinaison linéaire des autres vecteurs.
C. Somme de sous-espaces vectoriels en Maths Sup
1. Supplémentaires en dimension finie en Maths Sup
P1 : Soit ![]() un
un ![]() -espace vectoriel de dimension finie et
-espace vectoriel de dimension finie et ![]() un sous-espace vectoriel strict (c’est-à-dire distinct de
un sous-espace vectoriel strict (c’est-à-dire distinct de ![]() et de
et de ![]() ) de
) de ![]() .
.
Soit ![]() une base de
une base de ![]() . Il est possible par le théorème de la base incomplète de la compléter en une base de
. Il est possible par le théorème de la base incomplète de la compléter en une base de ![]() notée
notée ![]() .
.
Cette base est dite adaptée au sous-espace vectoriel ![]() .
.
Alors Vect![]() est un supplémentaire de
est un supplémentaire de ![]() .
.
P2 : Dans un ![]() -espace vectoriel
-espace vectoriel ![]() de dimension finie, tout s.e.v. admet un supplémentaire.
de dimension finie, tout s.e.v. admet un supplémentaire.
Pour tout supplémentaire ![]() de
de ![]() ,
,
![]() .
.
P3 : Soient ![]() un
un ![]() -espace vectoriel de dimension finie et
-espace vectoriel de dimension finie et ![]() et
et ![]() deux sous-espaces vectoriels de
deux sous-espaces vectoriels de ![]() .
.
Les propriétés suivantes sont équivalentes:
1. ![]()
2. ![]() et
et
![]()
3. ![]() et
et
![]()
2. Somme directe dans un espace vectoriel de dimension finie
T1 : Soit ![]() un
un ![]() -espace vectoriel de dimension finie. Si
-espace vectoriel de dimension finie. Si ![]() sont des sous-espaces vectoriels dont la somme
sont des sous-espaces vectoriels dont la somme ![]() est directe et si pour tout
est directe et si pour tout ![]() ,
, ![]() est une base de
est une base de ![]() ,
,
la famille ![]() obtenue par concaténation des bases
obtenue par concaténation des bases ![]() est une base de
est une base de ![]() .
.
On parlera de façon impropre de la « réunion » des bases ![]() .
.
La base ![]() est dite adaptée à la décomposition en somme directe
est dite adaptée à la décomposition en somme directe ![]() .
.
T2 : Soient ![]() un
un ![]() -espace vectoriel de dimension finie et
-espace vectoriel de dimension finie et ![]() des sous-espaces vectoriels de
des sous-espaces vectoriels de ![]() .
.
Si la somme des sous-espaces vectoriels ![]() est directe,
est directe,
![]() .
.
C : Soit ![]() un
un ![]() -espace vectoriel de dimension finie.
-espace vectoriel de dimension finie.
On suppose que la somme des sous espaces vectoriels ![]() ,
, ![]() , … ,
, … , ![]() est directe.
est directe.
![]() .
.
T3 : Soit ![]() un
un ![]() -espace vectoriel de dimension finie
-espace vectoriel de dimension finie ![]() de base
de base ![]() .
.
Soit ![]() et
et ![]() une partition de
une partition de ![]() . Pour tout
. Pour tout ![]() , on note
, on note ![]() Vect
Vect ![]() ; alors
; alors
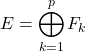 .
.
T4 : Soient ![]() des sous-espaces vectoriels du
des sous-espaces vectoriels du ![]() -espace vectoriel de dimension finie
-espace vectoriel de dimension finie ![]() .
.
a) 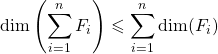
b) 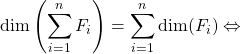 la somme des sous-espaces vectoriels
la somme des sous-espaces vectoriels ![]() est directe.
est directe.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
D. Applications linéaires en dimension finie en Maths Sup
1. Compléments des applications linéaires en dimensions finies
Dans ce §, ![]() et
et ![]() sont deux
sont deux ![]() -e.v.
-e.v.
P1 : Si ![]() est de dimension finie,
est de dimension finie, ![]() et
et ![]() sont isomorphes si, et seulement si,
sont isomorphes si, et seulement si, ![]()
P2 : Si ![]() et
et ![]() sont de dimension finie,
sont de dimension finie, ![]()
2. Rang d’une application linéaire en Maths Sup
D : Dans la suite, on suppose que ![]() et
et ![]() sont deux
sont deux ![]() -espaces vectoriels.
-espaces vectoriels.
On dit que ![]() est de rang fini lorsque l’espace vectoriel
est de rang fini lorsque l’espace vectoriel ![]() est de dimension finie.
est de dimension finie.
On appelle rang de ![]() la dimension de
la dimension de ![]() . On le note
. On le note ![]() .
.
P3 : Lorsque ![]() est de dimension finie et
est de dimension finie et ![]() ,
, ![]() est de rang fini.
est de rang fini.
Si ![]() est une base de
est une base de ![]() ,
, ![]() .
.
P4 : Soient ![]() 3
3 ![]() – espaces vectoriels,
– espaces vectoriels, ![]() et
et ![]()
a) Si ![]() et
et ![]() sont de rang fini,
sont de rang fini, ![]() est de rang fini et
est de rang fini et
![]()
b) Si ![]() est de rang fini et si
est de rang fini et si ![]() est un isomorphisme,
est un isomorphisme, ![]() est de rang fini et
est de rang fini et ![]() .
.
c) Si ![]() est de rang fini et si
est de rang fini et si ![]() est un isomorphisme,
est un isomorphisme, ![]() est de rang fini et
est de rang fini et ![]() .
.
Théorème du rang :
Soient ![]() et
et ![]() , deux
, deux ![]() -e.v. ,
-e.v. , ![]() étant de dimension finie et
étant de dimension finie et ![]()
![]()
![]() est isomorphe à tout supplémentaire
est isomorphe à tout supplémentaire ![]() de Ker
de Ker ![]() .
.
![]()
![]() est de dimension finie et
est de dimension finie et
![]() .
.
T1 : Soient ![]() et
et ![]() deux
deux ![]() -e.v. de même dimension
-e.v. de même dimension ![]() et
et ![]() .
.
Il y a équivalence entre :
a) ![]() est un isomorphisme de
est un isomorphisme de ![]() sur
sur ![]() ,
,
b) ![]() est injective,
est injective,
c) ![]() est surjective,
est surjective,
d) ![]() .
.
T2 : Soient ![]() et
et ![]() deux
deux ![]() -e.v. de même dimension
-e.v. de même dimension ![]() et
et ![]() .
.
Il y a équivalence entre
a) ![]() est un isomorphisme de
est un isomorphisme de ![]() sur
sur ![]()
b) ![]() ,
, ![]() ,
,
c) ![]() ,
, ![]() ,
,
Dans ce cas, ![]() .
.
Pour réussir en Maths Sup, les étudiants de prépa scientifique doivent s’organiser dans leurs révisions et s’obliger à travailler de façon régulière pendant leurs 2 années de prépa. Aussi, pour combler des lacunes ou tout simplement pour se remettre à niveau en maths, les stages intensifs en prépa scientifique sont très efficaces et les cours en ligne permettent également de maximiser cette progression. Les entraînements peuvent, par exemple, se faire sur les cours en ligne suivants :

