Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Exercices : Nombres complexes en MPSI, PCSI, PTSI

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices Corrigés

Cours en ligne de Maths en Maths Sup

Exercices – nombres complexes en MPSI, PCSI, PTSI

1. Modules et arguments

Question 1 (Vrai/faux)
Le complexe non nul $a(\cos b + \textrm{i} \, \sin b)$ a pour argument $b$

Question 2
a/ Redémontrer l’inégalité triangulaire et examiner le cas d’égalité .

b/ Si $z$ et $z'$ sont des complexes, $\quad \quad \quad \vert \, \vert z \vert - \vert z'\vert \, \vert \leq \vert z - z' \vert$

c/ Pour tout $(a , b) \in \mathbb{C}^2$ , montrer que $\quad \quad \vert a \vert + \vert b \vert \leq \vert a + b \vert + \vert a - b \vert$ .
Préciser les cas d’égalité

Question 3
$z$ est un imaginaire pur si, et seulement si,
a. $\displaystyle \textrm{Arg} z \equiv \frac {\pi} 2 \quad [2\, \pi]$ .
b. $z^2$ est un réel négatif ou nul.

Question 4
Si $z \in \mathbb{C}^*$ , $z$ et $\displaystyle \frac 1 z$ ont même partie réelle ssi $\vert z \vert = 1$ .

Question 5
Si $a, b$ et $c$ sont trois complexes de module $1$ , $\vert a b + a c + b c \vert = \vert a + b + c \vert$ .

2. Sur la fonction exponentielle

Question 1
Si $x$ est réel, $\overline {e ^{\textrm{i} \, x} } = e ^{ - \textrm{i} \, x}$

Question 2
Si $z$ est complexe, $\vert \textrm{e} ^{z} \vert = \textrm{e} ^{ \vert z \vert }$ .

Question 3
Si $z$ est complexe, $\vert \textrm{e} ^{z} \vert \leq \textrm{e} ^{ \vert z \vert }$ .

Question 4
Si $Z$ est un complexe non nul, les images des solutions de l’équation $\textrm{e}^z = Z$ sont alignées.

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

2. Sur les racines $n$ -ièmes

Question 1
Les racines $2n$ – ièmes de $1$ sont les complexes $\textrm{e}^{\textrm {i} \, k \, \pi/n}$ où
a) $k \in [\![0 , \, n - 1]\!]$
b) $k \in [\![0 , \, 2 \, n]\!]$
c) $k \in [\![- n + 1 , \, n]\!]$

Question 2
Si $\vert \omega \vert = 1$ , il existe $n \in \mathbb{N}^*$ , $\omega \in \mathbb{U}_n\,$ .

Question 3
Soit $n \in \mathbb{N}^*$ et $\omega \in \mathbb{U}_n\,$ .
$\{ \omega ^k \, , \, k \in [\![0 \, ,\, n - 1]\!] \} = \mathbb{U}_n \,$ .

Question 4
Soit $n \in \mathbb{N}^* \,$ , $\mathbb{U}_n = \{ \overline {z} \, , \, z \in \mathbb{U}_n \}$ .

Question 5
Soient $(m , n) \in \mathbb{N}^*$ .
$\mathbb{U}_m \subset \mathbb{U}_n$ ssi $m$ divise $n$ .

Question 6
Soit $n \in \mathbb{N}^*$ . Il existe une bijection de $\mathbb{U}_n$ sur l’ensemble $V_n$ des racines $n$ -ièmes de $- 1$

Question 7
Si $n$ est impair, $\mathbb{U}_n = \{ z ^2 \, , \, z \in \mathbb{U}_n \}$ .

Question 8
Les images $M_k$ des racines $n$ -ièmes de 1 sont les sommets d’un polygone régulier à $n$ côtés inscrit dans le cercle unité.

3. Manipulation de complexes

Exercice 1
Calculer les racines cubiques de $\displaystyle \frac {1 + \textrm{i} } {\sqrt{2}}$ . Les écrire sous forme cartésienne et en déduire la valeur de $\cos(\pi/12)$ et $\sin(\pi/12)$ .

Exercice 2
Si $a$ et $b$ sont deux complexes distincts de module 1,
$u = \displaystyle \frac {z + a\, b \, \, \overline {z} - a - b } {b - a}$ vérifie $u ^2 \leq 0$

Exercice 3
Résoudre le système $\vert z - 1 \vert = \vert z - 2\vert$ et $\textrm{Arg} (z + \textrm{i}) \equiv \textrm{Arg} (z - 1) \; \; [2 \pi]$ .

Exercice 4
Question 1
Soient deux complexes $z$ et $z'$ .
$\vert z + z' \vert ^2 + \vert z - z' \vert ^2 = a \left ( \vert z \vert ^2 + \vert z' \vert ^2 \right )$

Question 2
Interprétation géométrique du résultat de la question 1 lorsque $z$ et $z'$ sont non nuls.

Question 3
On suppose que $z\, z ' \neq 0$ et on note $u$ une racine carrée de $z\, z'$ .
$\displaystyle \left \vert \frac {z + z'} 2 + u \right \vert + \left \vert \frac {z + z'} 2 - u \right \vert$ $\quad \quad \quad \quad \quad \quad \quad \quad = a \left ( \vert z \vert + \vert z' \vert \right )$

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

4. Modules et arguments de trigonométrie

Exercice 1
a) Trouver la forme trigonométrique du complexe :
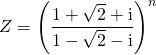$\quad \displaystyle Z = \left ( \frac {1 + \sqrt{2} + \textrm{i}} {1 - \sqrt{2} - \textrm{i}} \right ) ^n$ où $n \in \mathbb{N}^*$ .

Trouver la forme trigonométrique du complexe
$\quad \quad Z' = ( 1 + \cos t - \textrm{i} \, \sin t ) ^n$
si $n \in \mathbb{N}^*$ et $t \in [0 , 2 \pi[$ .

Exercice 2
Soit $a$ un réel.
On note $p = \sin(a) + \textrm{i} \, \cos(a)$ .
On note $Z_1$ et $Z_2$ les racines de l’équation $Z ^2 - 2 \, p \, Z + 1 = 0$ .

Question 1
Sans calculer explicitement $Z_1$ et $Z_2$ , comparer leurs modules et leurs arguments.

Question 2
Déterminer $a$ pour que $Z_1$ et $Z_2$ soient réels, puis pour qu’ils soient imaginai- res purs.

Question 3
Calculer les modules et arguments de $Z _ 1 - p$ et $Z_2 - p$ .

Question 4
Si $\cos a < 0$ , $Z_1 + \textrm{i}$ et $Z_2 + \textrm{i}$ ont même module à exprimer en fonction de $a$ .

5. Équations

Exercice 1
Résoudre dans $\mathbb{C}$ :
$\quad 2 \, z^2 - 2(2 +\, \textrm{i} ) z + 22 \, \textrm{i} - 3 = 0$ .

Exercice 2
Résoudre $\; \; z^4 + 2(1 - 4 \, \textrm{i}) z^2 +33 +56 \, \textrm{i} = 0$ .

Exercice 3
Résoudre lorsque $z$ est un complexe, l’équation
$\quad \quad \textrm{e}^{ 4 z} + 3\, \textrm{e}^{ 3 z} + 8\, \textrm{e}^{ z} + 24 = 0$ .

Exercice 4
Résoudre dans $\mathbb{C}$ l’équation
$\quad \quad Z^{2\, n} - 2\, Z^n \, \sin(t) + 1 = 0$ ,
où $n \in \mathbb{N}$ et $n \geq 2$ .

Exercice 5
Oral Mines Telecom MP 2018
Résoudre l’équation $z^3 + (1 + \textrm{i} ) z^2 + (4 - \, \textrm{i} ) z + 12 - 6 \, \textrm{i} = 0$ sachant qu’elle a une racine réelle.
Que dire du triangle formé par les images des trois racines ?

Exercice 6
Question 1
Quel est l’ensemble des nombres complexes $z$ tels que $\quad \quad \quad \quad \vert z -1\vert = \vert \overline{z} +1\vert$ ?

Question 2
Pour tout $n \in \mathbb{N}^*$ , l’équation $(z - 1) ^n = (\overline{z} + 1) ^n$ n’a pas de solution.

Exercice 7
Soit $n \in \mathbb{N}$ , $n \geq 2$ et $a \in [0 , \, 2 \pi[$
Résoudre l’équation $(E)$ : $\quad \quad (1 + z)^n = \textrm{e} ^{\textrm{i} \, a} (1 - z) ^n$ .

Profitez-en également, pour réviser et vous entraîner sur d’autres exercices et cours en ligne de Maths pour les étudiants de Maths Sup :