Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur dénombrement en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices de dénombrements
1. Application directe des résultats de cours
2. Un peu plus élaborés, mais pas trop
3. Sans urne et sans carte
4. Des couples de parties de ![]()
5. Des formules obtenues par dénombrement
6. Équations entières et suites croissantes
7. Mots de ![]() lettres à partir de
lettres à partir de ![]() et
et ![]()
8. Un exercice sur les surjections
9. Dénombrement des involutions
10. Mots de Dyck
⚠️ Dans tous les exercices ne vous contentez pas d’une valeur numérique. Il faut justifier vos résultats.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Des dénombrements simples
1. Quel est le nombre de codes d’un antivol à 4 chiffres choisis entre 1 et 5 ?
Même question si les chiffres doivent être distincts .
Correction :
![]() Le nombre de codes d’un antivol à 4 chiffres est le nombre d’applications de
Le nombre de codes d’un antivol à 4 chiffres est le nombre d’applications de ![]() dans l’ensemble
dans l’ensemble ![]() donc est égal à
donc est égal à ![]() .
.
![]() Dans le deuxième cas, c’est le nombre de 4-listes sans répétition des 6 chiffres de 1 à 5 soit
Dans le deuxième cas, c’est le nombre de 4-listes sans répétition des 6 chiffres de 1 à 5 soit ![]()
2. Quel est le nombre de mots de passe de 4 lettres formés uniquement de consonnes ?
Même question si les consonnes doivent être distinctes.
Correction :
![]() Le nombre de mots de passe de 4 lettres est le nombre d’applications de
Le nombre de mots de passe de 4 lettres est le nombre d’applications de ![]() dans l’ensemble des 20 consonnes donc est égal à
dans l’ensemble des 20 consonnes donc est égal à ![]() .
.
![]() Dans le deuxième cas, c’est le nombre de 4-listes sans répétition des 20 consonnes soit
Dans le deuxième cas, c’est le nombre de 4-listes sans répétition des 20 consonnes soit ![]() .
.
3. Quel est le nombre de tiercés (dans l’ordre) que l’on peut jouer dans une course de 20 chevaux ?
Correction : Le nombre de tiercés (dans l’ordre) que l’on peut jouer dans une course de 20 chevaux est le nombre de 3-listes sans répétition des 20 chevaux soit ![]() .
.
4. Quel est le nombre de façons de choisir un groupes de ![]() élèves dans une classe de
élèves dans une classe de ![]() élèves pour faire un exposé ?
élèves pour faire un exposé ?
a) ![]() b)
b) ![]() c)
c) ![]()
Correction : Le nombre de façons de choisir un groupe de ![]() élèves dans une classe de
élèves dans une classe de ![]() élèves pour faire un exposé est le nombre de parties à
élèves pour faire un exposé est le nombre de parties à ![]() éléments parmi
éléments parmi ![]() soit
soit ![]() .
.
5. Quel est le nombre de grilles au loto (5 numéros de 1 à 49 et 1 numéro chance de 1 à 10) ?
6. Quel est le nombre de façons de ranger les ![]() éléments d’un ensemble
éléments d’un ensemble ![]()
7. Quel est le nombre de façons de ranger les ![]() éléments de
éléments de ![]() de façon à ce que les éléments 1 à
de façon à ce que les éléments 1 à ![]() soient côte à côte.
soient côte à côte.
8. Quel est le nombre d’entiers de ![]() chiffres contenant un seul
chiffres contenant un seul ![]() et un seul
et un seul ![]() ?
?
9. Quel est le nombre d’anagrammes du mot « ENTENTE »
10. Combien de mots peut on écrire avec le mot « TOULOUSE » si les consonnes doivent être placées en 1-ère, 4-ème et 7-ème position ?
11. Il y a ![]() façons de placer
façons de placer ![]() personnes autour d’une table ronde
personnes autour d’une table ronde
12. Il y a ![]() manières de placer
manières de placer ![]() couples autour d’une table ronde en alternant un homme et une femme
couples autour d’une table ronde en alternant un homme et une femme
13. Quel est le nombre ![]() de dominos (2 chiffres de
de dominos (2 chiffres de ![]() à
à ![]() qui peuvent être répétés) ?
qui peuvent être répétés) ?
Quel est le nombre ![]() de triominos (3 chiffres de
de triominos (3 chiffres de ![]() à
à ![]() qui peuvent être répétés aux sommets d’un triangle équilatéral) ?
qui peuvent être répétés aux sommets d’un triangle équilatéral) ?
2. D’autres dénombrements
Exercice 1
Dans cet exercice, on effectue 3 tirages successifs et sans remise dans un ensemble contenant ![]() boules blanches,
boules blanches, ![]() rouges et
rouges et ![]() vertes.
vertes.
a) Quel est le nombre de tirages tricolores ?
Correction : Le nombre de façons d’obtenir une boule blanche puis une rouge puis une verte est égal à ![]() .
.
Le nombre de façons d’obtenir un tirage tricolore est égal à ![]() (car on a
(car on a ![]() façons de choisir l’ordre de tirage des trois couleurs).
façons de choisir l’ordre de tirage des trois couleurs).
b) Quel est le nombre de tirages bicolores ?
Correction : ![]() Le nombre
Le nombre ![]() de tirages monocolores est égal au nombre de tirages blancs plus le nombre de tirages rouges plus le nombre de tirages verts soit
de tirages monocolores est égal au nombre de tirages blancs plus le nombre de tirages rouges plus le nombre de tirages verts soit ![]()
![]() .
.
![]() Le nombre
Le nombre ![]() de tirages est égal à
de tirages est égal à ![]() où
où ![]() .
.
Exercice 2
On tire 5 cartes d’un jeu de 32 cartes. Quel est le nombre de mains contenant 2 as ?
Correction : On choisit 2 as parmi 4 de ![]() façons.
façons.
Puis on choisit 3 cartes parmi les ![]() cartes sans as de
cartes sans as de ![]() façons.
façons.
Le nombre de mains contenant deux as est égal à ![]() .
.
Exercice 3
Quel est le nombre de mains de 4 cartes d’un jeu de 32 cartes contenant 2 rois ou 3 dames ?
Correction :
On ne peut pas avoir deux rois et trois dames en même temps dans une main de 4 cartes.
On note ![]() l’ensemble des mains contenant 2 Rois et
l’ensemble des mains contenant 2 Rois et ![]() l’ensemble des mains contenant 3 dames.
l’ensemble des mains contenant 3 dames.
![]()
![]()
car on choisit 2 rois parmi 4 de ![]() façons puis 2 cartes parmi les 28 qui restent de
façons puis 2 cartes parmi les 28 qui restent de ![]() façons.
façons.
![]()
![]()
car on choisit 3 dames parmi 4 de ![]() façons puis 1 carte parmi les 28 qui restent de
façons puis 1 carte parmi les 28 qui restent de ![]() façons.
façons.
![]() car
car ![]() .
.
⚠️ Aviez -vous pensé à écrire que les deux ensembles sont disjoints ?
Exercice 4
Quel est le nombre de mains de 4 cartes issues d’un jeu de 32 cartes contenant 2 rois ou 3 trèfles ?
Correction :
On peut obtenir une main contenant le roi de trèfle.
Soit ![]() l’ensemble des mains de 4 cartes contenant
l’ensemble des mains de 4 cartes contenant ![]() rois et
rois et ![]() l’ensemble des mains de 4 cartes contenant
l’ensemble des mains de 4 cartes contenant ![]() trèfles.
trèfles.
![]()
![]()
car on choisit ![]() rois parmi
rois parmi ![]() de
de ![]() façons puis
façons puis ![]() cartes parmi les
cartes parmi les ![]() qui restent de
qui restent de ![]() façons.
façons.
![]()
![]()
car on choisit ![]() trèfles parmi
trèfles parmi ![]() de
de ![]() façons puis
façons puis ![]() carte parmi les
carte parmi les ![]() qui restent de
qui restent de ![]() façons.
façons.
![]()
![]()
C’est l’ensemble des mains contenant le roi de trèfle, un autre roi et ![]() autres trèfles.
autres trèfles.
On choisit un roi qui n’est pas de trèfle (![]() choix), deux trèfles différents du roi de
choix), deux trèfles différents du roi de ![]() façons.
façons.
![]()
![]() .
.
⚠️ Aviez-vous vu que les ensembles ne sont pas disjoints ?
Exercice 5
Quel est le nombre de mains de 5 cartes issues d’un jeu de 32 cartes contenant au moins un as ?
Exercice 6
Quel est le nombre de mains de 5 cartes d’un jeu de 32 contenant au moins 2 trèfles ?
Exercice 7
Quel est le nombre de mains de 5 cartes d’un jeu de 32 cartes contenant 1 roi et au moins un pique.
Exercice 8
On souhaite ranger sur une étagère 4 livres de mathématiques (distincts), 6 livres de physique, et 3 de chimie.
Question 1
De combien de façons peut-on effectuer ce rangement, si les livres doivent être groupés par matières ?
Question 2
De combien de façons peut-on effectuer ce rangement, si seuls les livres de mathématiques doivent être groupés ?
Exercice 9
Quel est le nombre de matrices symétriques d’ordre ![]() dont tous les éléments sont dans
dont tous les éléments sont dans ![]() ?
?
Exercice 10
On dispose de 2 jeux de jetons numérotés de 1 à ![]() , l’un blanc, l’autre noir, on les place dans une urne.
, l’un blanc, l’autre noir, on les place dans une urne.
Question 1
On prend au hasard ![]() (
(![]() ) jetons en même temps.
) jetons en même temps.
Nombre de tirages donnant des jetons ayant des numéros tous distincts.
Question 2
Avec les hypothèses de la question 1, nombre de façons d’avoir obtenu deux jetons portant le même numéro.
Question 3
On tire maintenant les jetons 2 par 2 sans remise. Nombre de tirages possibles.
Question 4
Dans cette question, on tire les ![]() jetons l’un après l’autre.
jetons l’un après l’autre.
Quel est le nombre de tirages donnant une alternance de couleurs ?
3. Sans urne et sans carte
Exercice 1
Soit ![]() .
.
Le nombre de solutions dans ![]() de l’équation
de l’équation ![]() est égal à ?
est égal à ?
Correction : C’est l’ensemble ![]() .
.
Il a ![]() éléments.
éléments.
Question 2
Le nombre de solutions dans ![]() de l’équation
de l’équation ![]() est égal à
est égal à ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : On note ![]() l’ensemble des solutions entières de cette équation
l’ensemble des solutions entières de cette équation
et si ![]() l’ensemble des solutions entières telles que
l’ensemble des solutions entières telles que ![]() .
.
On écrit 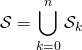 .
.
Les ensembles ![]() sont2 à 2 disjoints.
sont2 à 2 disjoints.
![]() est en bijection avec
est en bijection avec ![]()
![]() par la question 1.
par la question 1.
On écrit 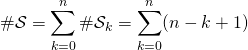
en posant ![]() ,
,
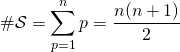 .
.
Exercice 2.
Soit ![]() .
.
Question 1
Quel est le nombre de façons de régler au café une somme de ![]() euros en n’utilisant que des pièces de 1 et 2 euros ?
euros en n’utilisant que des pièces de 1 et 2 euros ?
Correction :
Si
donc
Question 2
Nombre de façons de payer dans un distributeur une somme de ![]() euros en n’utilisant que des pièces de 1 et 2 euros
euros en n’utilisant que des pièces de 1 et 2 euros
Correction : On note ![]() l’ensemble des paiements dans le distributeur pour une somme de
l’ensemble des paiements dans le distributeur pour une somme de ![]() euros.
euros.
Soit ![]() . Si
. Si ![]() , on introduit
, on introduit ![]() l’ensemble des paiements au distributeur où l’on a rentré
l’ensemble des paiements au distributeur où l’on a rentré ![]() pièces de 2 euros et
pièces de 2 euros et ![]() pièces de 1 euro.
pièces de 1 euro.
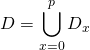 .
.
Ces ensembles étant deux à deux disjoints, 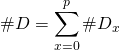 .
.
![]()
car on choisit les ![]() moments parmi
moments parmi ![]() où l’on rentre les pièces de
où l’on rentre les pièces de ![]() euros.
euros.
donc 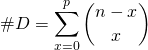 .
.
Exercice 3
Soit ![]() un ensemble de cardinal
un ensemble de cardinal ![]() .
.
La somme des cardinaux des parties de ![]() est égale à
est égale à
Correction :
Si ![]() , on note
, on note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() ayant
ayant ![]() éléments.
éléments.
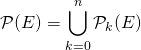 .
.
On a introduit une partition, donc
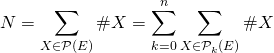
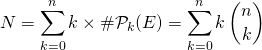
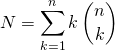 .
.
Puis 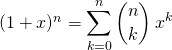
et par dérivation,
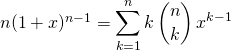
Si ![]() ,
, ![]() .
.
Exercice 4
Soit ![]() un ensemble de cardinal
un ensemble de cardinal ![]() .
.
Le nombre de partitions de ![]() en 2 parties est égal à
en 2 parties est égal à
Correction : On remarque que la donnée d’une partie ![]() non vide et différente de
non vide et différente de ![]() définit une partition
définit une partition ![]()
et que ![]() .
.
Il y a ![]() parties de
parties de ![]() non vides et différentes de
non vides et différentes de ![]() .
.
La même partition étant obtenue 2 fois, le nombre de partitions est égal à ![]() .
.
4. Couples de parties de 
Soit ![]() un ensemble de cardinal
un ensemble de cardinal ![]() .
.
Question 1
Le nombre de couples ![]() de parties de
de parties de ![]() est égal à
est égal à
Correction : C’est ![]() .
.
Question 2
Le nombre de couples ![]() de parties de
de parties de ![]() telles que
telles que ![]() est égal à ?
est égal à ?
Correction : Soit ![]()
et ![]()
![]()
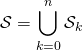 , les ensembles étant 2 à 2 disjoints,
, les ensembles étant 2 à 2 disjoints, 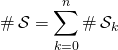 .
.
Pour déterminer ![]() ,
,
![]() On choisit une partie
On choisit une partie ![]() de
de ![]() ayant
ayant ![]() éléments de
éléments de ![]() façons.
façons.
![]() On choisit
On choisit ![]() : il y a
: il y a ![]() façons de le faire.
façons de le faire.
Donc ![]() .
.
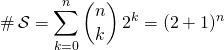
par le binôme de Newton.
Question 3
Le nombre de couples ![]() de parties de
de parties de ![]() telles que
telles que ![]() et
et ![]() est égal à
est égal à ![]() Vrai ou Faux ?
Vrai ou Faux ?
Correction : C’est le nombre ![]() de couples
de couples ![]() de
de ![]() tels que
tels que ![]() diminué du nombre de couples
diminué du nombre de couples ![]() de
de ![]() qui est égal à
qui est égal à ![]() .
.
On obtient donc ![]()
Question 4
Le nombre de couples ![]() de parties de
de parties de ![]() telles que
telles que ![]() est égal à
est égal à ![]() Vrai ou Faux ?
Vrai ou Faux ?
Correction : On note ![]() cet ensemble et si
cet ensemble et si ![]() ,
, ![]() l’ensemble des couples
l’ensemble des couples ![]() tels que
tels que ![]() et
et ![]() .
.
alors 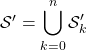 , les ensembles étant 2 à 2 disjoints,
, les ensembles étant 2 à 2 disjoints, 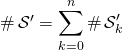
Pour déterminer ![]() ,
,
![]() on choisit une partie
on choisit une partie ![]() ayant
ayant ![]() éléments de
éléments de ![]() façons.
façons.
![]() on choisit
on choisit ![]() : il y a
: il y a ![]() façons de le faire
façons de le faire
donc ![]() .
.
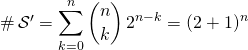
par le binôme de Newton.
⚠️ à ne pas confondre avec le nombre de couples de parties ![]() de
de ![]() telles que
telles que ![]() et
et ![]() qui est égal à
qui est égal à ![]() car c’est le nombre de couples
car c’est le nombre de couples ![]() où
où ![]() .
.
Question 5
Le nombre de couples ![]() de parties de
de parties de ![]() telles que
telles que ![]() est égal à ?
est égal à ?
Correction : On note ![]() cet ensemble et si
cet ensemble et si ![]() ,
, ![]() l’ensemble des couples
l’ensemble des couples ![]() tels que
tels que ![]() et
et ![]() .
.
alors 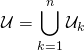 , les ensembles étant 2 à 2 disjoints,
, les ensembles étant 2 à 2 disjoints, 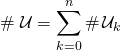 .
.
Pour déterminer ![]() ,
,
![]() On choisit l’élément
On choisit l’élément ![]() commun à
commun à ![]() et
et ![]() :
: ![]() choix
choix
![]() On choisit les
On choisit les ![]() autres éléments de
autres éléments de ![]() de
de ![]() façons.
façons.
![]() On choisit
On choisit ![]() : il y a
: il y a ![]() façons de le faire.
façons de le faire.
Donc ![]() .
.
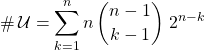
en posant ![]()
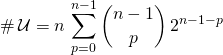 .
.
Par le binôme de Newton,
![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
5. Des formules obtenues par des dénombrements
Exercice 1
Si ![]() , démontrer que
, démontrer que
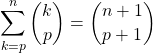 .
.
par un raisonnement de dénombrement
Correction : On note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() formées de
formées de ![]() éléments.
éléments.
![]() Pour tout
Pour tout ![]() , on note
, on note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() à
à ![]() éléments dont le maximum est égal à
éléments dont le maximum est égal à ![]() .
.
![]() ssi
ssi ![]() .
.
![]() L’ensemble des
L’ensemble des ![]() forme une partition de
forme une partition de ![]() .
.
Se donner un élément de ![]() revient à choisir une partie de
revient à choisir une partie de ![]() éléments dans
éléments dans ![]() ce qui se fait de
ce qui se fait de ![]() façons et à lui ajouter
façons et à lui ajouter ![]() .
.
![]()
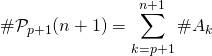 .
.
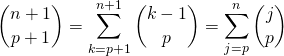
avec ![]() .
.
👍 On peut aussi démontrer cette relation ainsi :
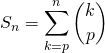
Par la formule du triangle de Pascal (valable si ![]() ),
),
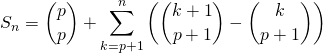
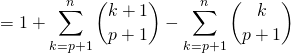
avec ![]() ,
,
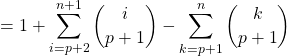
![]() .
.
Exercice 2
Soient ![]() et
et ![]() trois entiers naturels non nuls avec
trois entiers naturels non nuls avec ![]() .
.
En utilisant un raisonnement de dénombrement, démontrer la formule de Vandermonde :
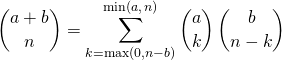 .
.
Correction :
Soient ![]() et
et ![]() .
.
![]() et
et ![]() sont disjoints et ont respective- ment
sont disjoints et ont respective- ment ![]() et
et ![]() éléments.
éléments. ![]() .
.
![]() On note
On note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() ayant
ayant ![]() éléments.
éléments. ![]() .
.
![]() On note
On note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() formées de
formées de ![]() éléments dans
éléments dans ![]() et
et ![]() dans
dans ![]() .
.
L’ensemble ![]() est non vide
est non vide
ssi ![]() et
et ![]()
ssi ![]() .
.
Les ensembles ![]()
forment une partition de ![]() .
.
![]() car on doit choisir
car on doit choisir ![]() éléments parmi
éléments parmi ![]() et
et ![]() éléments parmi
éléments parmi ![]() .
.
![]()
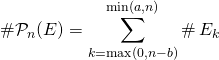
soit 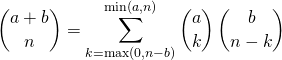 .
.
👍 L’utilisation la plus fréquente est dans le cas ![]() et on obtient
et on obtient
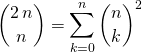
car ![]() .
.
Exercice 3
Soit ![]() .
.
Question 1
Soit ![]() .
.
Déterminer le nombre d’applications strictement croissantes de ![]() dans
dans ![]() .
.
Correction : On note ![]() l’ensemble des applications strictement croissantes de
l’ensemble des applications strictement croissantes de ![]() dans
dans ![]() .
.
Se donner une application strictement croissante de ![]() dans
dans ![]() revient à choisir une partie de
revient à choisir une partie de ![]() à
à ![]() éléments et à la ranger par ordre strictement croissant.
éléments et à la ranger par ordre strictement croissant.
Il y a donc ![]() applications strictement croissantes de
applications strictement croissantes de ![]() dans
dans ![]() .
.
Exercice 3 (suite)
Question 2
Déterminer le nombre d’applications strictement croissantes de ![]() dans
dans ![]() telles que
telles que ![]() .
.
Correction : Pour se donner une telle application, on définit une application strictement croissante de ![]() dans
dans ![]() , il y a
, il y a ![]() applications de ce type et on impose
applications de ce type et on impose ![]() .
.
Question 3
Si ![]() et
et ![]() , déterminer le nombre d’applications strictement croissantes de
, déterminer le nombre d’applications strictement croissantes de ![]() dans
dans ![]() telles que
telles que ![]()
Correction : On note ![]() l’ensemble des applica- tions vérifiant les conditions de l’énoncé.
l’ensemble des applica- tions vérifiant les conditions de l’énoncé.
Une telle application est entièrement définie par sa restriction à ![]() et sa restriction à
et sa restriction à ![]() .
.
![]() On détermine d’abord le nombre d’applications strictement croissantes de
On détermine d’abord le nombre d’applications strictement croissantes de ![]() dans
dans ![]() telles que
telles que ![]() lorsque
lorsque ![]() .
.
En utilisant la question 2, il y en a ![]() .
.
![]() Puis on détermine le nombre d’applications strictement croissantes de
Puis on détermine le nombre d’applications strictement croissantes de ![]() dans
dans ![]() .
.
Le problème a une solution ssi l’on peut choisir les ![]() images dans un ensemble de
images dans un ensemble de ![]() éléments donc ssi
éléments donc ssi ![]() ssi
ssi ![]() .
.
Il y en a ![]() .
.
Donc si ![]() ,
, ![]() .
.
Question 4
Si ![]() est dans
est dans ![]() , en déduire la valeur de
, en déduire la valeur de
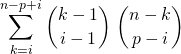 .
.
Correction : On écrit 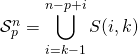 .
.
On a une réunion d’ensembles 2 à 2 disjoints, donc
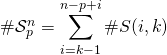
soit 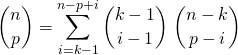 .
.
6. Équations entières et suites croissantes
Exercice 1
Soit ![]() .
.
Question 1
Le nombre de solutions entières de l’équation ![]() est égal à
est égal à ![]() . Vrai ou faux ?
. Vrai ou faux ?
Correction : On peut démontrer ce résultat en considérant le nombre de façons de répartir ![]() objets identiques dans
objets identiques dans ![]() tiroirs (
tiroirs (![]() est alors le nombre d’objets dans le tiroir
est alors le nombre d’objets dans le tiroir ![]() ).
).
On note les ![]() objets par un
objets par un ![]() et les
et les ![]() séparations entre les différents tiroirs par un | .
séparations entre les différents tiroirs par un | .
Il s’agit donc de placer les ![]() séparations sur
séparations sur ![]() places, ce qui se fait en choisissant
places, ce qui se fait en choisissant ![]() places parmi
places parmi ![]() donc il y a
donc il y a ![]() choix.
choix.
On termine en utilisant :
![]() .
.
Question 2
Le nombre de solutions entières de l’inéquation ![]()
est égal à ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() On note
On note ![]() l’ensemble des solutions entières de
l’ensemble des solutions entières de ![]()
et ![]() l’ensemble des solutions entières de
l’ensemble des solutions entières de ![]() .
.
Si ![]() , il est évident que
, il est évident que
![]()
et que les 2 ensembles sont disjoints.
![]()
si ![]() ,
, ![]()
par la première question,
![]()
![]()
et ![]() .
.
![]() Première méthode : par télescopage
Première méthode : par télescopage
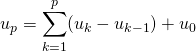
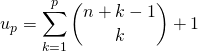
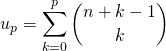
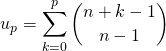
En posant ![]() ,
,
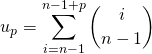
Par application de l’exercice 1 du § I
![]() .
.
![]() Deuxième méthode.
Deuxième méthode.
Si ![]() est fixé, on note
est fixé, on note
![]() ,
, ![]() .
.
![]()
![]() .
.
On a prouvé ![]() .
.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
Par la formule ![]()
![]()
![]()
Par ![]() :
:
![]()
par le triangle de Pascal :
![]()
ce qui prouve ![]() .
.
La propriété est démontrée par récurrence.
Exercice 2
Soit ![]() ,
,
![]() est le nombre de listes croissantes de
est le nombre de listes croissantes de ![]() éléments de
éléments de ![]() .
.
Vrai ou Faux ?
Correction : Soit ![]()
![]() .
.
![]() 1ère méthode :
1ère méthode :
On note 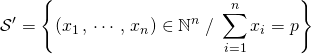 .
.
Soit ![]()
où si ![]() ,
, ![]() est le
est le ![]() -uplet tel que les
-uplet tel que les ![]() premiers éléments soient des
premiers éléments soient des ![]() , les
, les ![]() suivants soient des
suivants soient des ![]() , … , et les
, … , et les ![]() derniers soient des
derniers soient des ![]()
(![]() est une suite croissante de
est une suite croissante de ![]() entiers compris entre
entiers compris entre ![]() et
et ![]() ).
).
![]() est une bijection de
est une bijection de ![]() sur
sur ![]() , l’antécédent de
, l’antécédent de ![]() de
de ![]() est le
est le ![]() -uplet égal à
-uplet égal à ![]() où
où ![]() est le nombre de
est le nombre de ![]() dans
dans ![]() , avec
, avec ![]() .
.
Alors ![]() , il suffit d’utiliser le résultat de la question 1 de l’exercice 1,
, il suffit d’utiliser le résultat de la question 1 de l’exercice 1, ![]() .
.
![]() 2ème méthode : On note
2ème méthode : On note ![]() l’ensemble des
l’ensemble des ![]() tels que
tels que 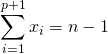 .
.
Si ![]() , on définit
, on définit
![]()
![]()
![]()
![]() avec par télescopage :
avec par télescopage : 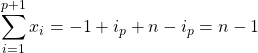 .
.
Donc ![]() .
.
![]() Il est simple de prouver que
Il est simple de prouver que ![]() est injective.
est injective.
![]() Soit
Soit ![]() .
.
On définit le ![]() -uplet
-uplet ![]() égal à
égal à
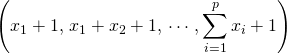
![]() est une famille croissante de
est une famille croissante de ![]() entiers strictement positifs vérifiant :
entiers strictement positifs vérifiant :
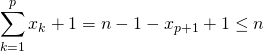 ,
,
donc ![]() et
et ![]() .
.
L’application ![]() est surjective.
est surjective.
![]() étant bijective :
étant bijective :
![]()
![]() d’après l’exercice 1.
d’après l’exercice 1.
7. Mots de  lettres
lettres
Si ![]() , soit
, soit ![]() l’ensemble des mots formés de
l’ensemble des mots formés de ![]() lettres ne contenant que les lettres
lettres ne contenant que les lettres ![]() et
et ![]() et tels qu’il n’y ait pas deux
et tels qu’il n’y ait pas deux ![]() consécutifs.
consécutifs.
On note ![]() .
.
Question 1.
Déterminer ![]() .
.
Correction : ![]()
![]()
et ![]() ,
,
donc ![]() .
.
Question 2
Si ![]() .
.
Vrai ou faux ?
Correction : On note ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() qui se terminent par
qui se terminent par ![]() donc qui se terminent par
donc qui se terminent par ![]() et
et ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() qui se terminent par
qui se terminent par ![]() .
.
![]() , on a ainsi écrit une partition de
, on a ainsi écrit une partition de ![]() donc
donc
![]() .
.
![]()
![]() ,
, ![]()
Il est évident que ![]() est une bijection donc
est une bijection donc ![]() .
.
![]()
![]() ,
, ![]()
Il est évident que ![]() est une bijection donc
est une bijection donc ![]() .
.
On a donc prouvé que ![]() .
.
Question 3
Calculer ![]() .
.
Correction : On a une suite récurrente linéaire d’ordre 2 d’équation caractéristique :
![]() avec
avec ![]() et
et ![]() .
.
Il existe donc deux réels ![]() et
et ![]() tels que si
tels que si ![]()
👍 : il est plus simple d’utiliser des puissances ![]() que des puissances
que des puissances ![]() dans les calculs qui suivent car on utilise
dans les calculs qui suivent car on utilise ![]() et
et ![]() pour déterminer
pour déterminer ![]() et
et ![]() .
.
On résout donc le système
![]()
![]()
![]()
![]()
![]()
![]()
![]() et
et ![]() .
.
Donc ![]() est égal à
est égal à ![]() .
.
8. Sur les surjections
Si ![]() , on note
, on note ![]() .
.
Soient ![]() et
et ![]() deux entiers naturels non nuls. On note
deux entiers naturels non nuls. On note ![]() le nombre de surjections de
le nombre de surjections de ![]() dans
dans ![]() .
.
Question 1
Donner les valeurs de ![]() et de
et de ![]() si
si ![]() .
.
Question 2
Calculer ![]() .
.
Question 3
Calculer ![]() .
.
Question 4
Calculer ![]() .
.
Question 5
Si ![]() ,
,
![]()
![]() .
.
Question 6
Montrer que 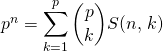
Question 7
Si ![]() ,
,
![]() est égal à
est égal à ![]() .
.
Question 8
Si ![]() ,
,
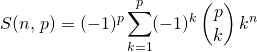 .
.
Question 9
Soit ![]() un ensemble de
un ensemble de ![]() éléments. Déterminer le nombre de partitions de
éléments. Déterminer le nombre de partitions de ![]() en
en ![]() parties.
parties.
9. Dénombrement des involutions
On dit que ![]() est une involution de
est une involution de ![]() lorsque
lorsque ![]() vérifie
vérifie ![]() .
.
Si ![]() , on note
, on note ![]() ,
, ![]() l’ensemble des involutions de
l’ensemble des involutions de ![]() et
et ![]() .
.
Question 1
Toute involution est une bijection.
Question 2
Déterminer ![]() et donner la réponse sous la forme x,y,z.
et donner la réponse sous la forme x,y,z.
Question 3
Si ![]() , exprimer
, exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() .
.
Question 4
La relation de la question 3 est encore vraie si l’on convient que ![]() .
.
Question 5
Montrer que pour tout ![]() ,
,
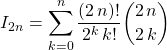
![]() et
et 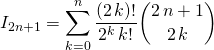 .
.
10. Mots de Dyck
On appelle » mot de Dyck » une chaîne de ![]() caractères,
caractères, ![]() , formée de
, formée de ![]() lettres
lettres ![]() et
et ![]() lettres
lettres ![]() , telle que, lorsque l’on dénombre les lettres de gauche à droite, en s’arrêtant à une lettre du mot, le nombre de
, telle que, lorsque l’on dénombre les lettres de gauche à droite, en s’arrêtant à une lettre du mot, le nombre de ![]() soit toujours supérieur ou égal au nombre de
soit toujours supérieur ou égal au nombre de ![]() . Ainsi, le seul mot de Dyck de longueur
. Ainsi, le seul mot de Dyck de longueur ![]() est :
est : ![]() . Les mots de Dyck de longueur 4 sont :
. Les mots de Dyck de longueur 4 sont : ![]() et
et ![]() .
.
![]() et
et ![]() sont des mots de Dyck, alors que
sont des mots de Dyck, alors que ![]() et
et ![]() n’en sont pas.
n’en sont pas.
Pour tout entier ![]() , on désigne par
, on désigne par ![]() le nombre de mots de Dyck de
le nombre de mots de Dyck de ![]() lettres.
lettres.
Question 1
Calculer ![]() .
.
Question 2
Montrer que ![]() .
.
👍 ![]() est appelé le
est appelé le ![]() -ième nombre de Catalan.
-ième nombre de Catalan.
Question 3 : Une application
Une particule se déplace sur une droite graduée en partant de l’origine et en se déplaçant à chaque minute d’une unité vers la droite ou vers la gauche.
Le nombre de façons de revenir pour la première fois à l’instant ![]() en
en ![]() est égal à
est égal à ![]()
Les questions suivantes sont plus compliquées
Question 4.
Soit ![]() et
et ![]() l’ensemble des mots de Dyck des mots de Dyck de longueur
l’ensemble des mots de Dyck des mots de Dyck de longueur ![]() tels que l’on obtienne autant de
tels que l’on obtienne autant de ![]() que de
que de ![]() pour la première fois au rang
pour la première fois au rang ![]() .
.
Montrer que ![]() .
.
Question 5
On pose : ![]() . Montrer que, pour tout entier
. Montrer que, pour tout entier 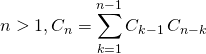 .
.
Utilisez ces cours en ligne de mathématiques au programme de MPSI, PCSI et PTSI pour vos révisions et vos entraînements. Chaque cours reprend les notions et les méthodes à connaître parfaitement pour progresser efficacement. Vous pouvez d’ores et déjà avancer dans le programme en révisant les chapitres de fin d’année :

