Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les Développements limités en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Exercices corrigés : Développement asymptotique
Plan des exercices sur le développement asymptotique :
1. Déduction d’une somme d’un calcul de DL
2. Démonstration d’une équivalence
3. Développement asymptotique d’une suite
4. Développement asymptotique d’une suite implicite, exemple 1
5. Développement asymptotique d’une suite implicite, exemple 2
6. Sur le DL de la fonction th
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Déduction d’une somme à l’aide des DL en MPSI, PCSI, MP2I et PTSI
Si ![]() et
et ![]() sont deux entiers naturels, on note
sont deux entiers naturels, on note 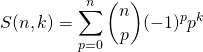 .
.
Calculer ![]() en distinguant les cas
en distinguant les cas ![]() ,
, ![]() et
et ![]() et
et ![]() .
.
Indication : dériver la fonction ![]() .
.
Correction :
![]() En utilisant le binôme de Newton :
En utilisant le binôme de Newton :
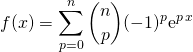
puis en dérivant ![]() fois :
fois :
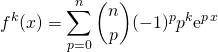
et en prenant la valeur en ![]() :
:
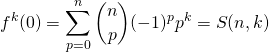 .
.
![]() On calcule ensuite le DL de
On calcule ensuite le DL de ![]() à l’ordre
à l’ordre ![]()
Pas de panique, il doit y avoir une astuce
![]()
![]()
grâce à la multiplication par ![]() , le calcul du DL de
, le calcul du DL de ![]() à l’ordre 2 suffit à donner le DL de
à l’ordre 2 suffit à donner le DL de ![]() à l’ordre
à l’ordre ![]()
![]()
![]()
![]()
donc
![]()
![]() Grâce à a formule de Taylor Young, on obtient par unicité du DL
Grâce à a formule de Taylor Young, on obtient par unicité du DL
![]() si
si ![]() soit
soit ![]()
![]()
![]()
![]()
![]()
![]()
soit ![]() .
.
![]()
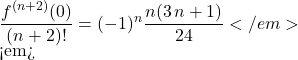 soit
soit ![]()
Question 2
Écrire un développement asymptotique en ![]() de
de ![]()
2. Pour démontrer une équivalence avec les développements limités en sup
Question 1
Soit ![]() .
.
Montrer que ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
Trouver un équivalent simple de ![]() en
en ![]() .
.
Correction de la question 1 :
![]() est continue sur
est continue sur ![]() ,
, ![]() si
si
![]() , donc
, donc ![]() est strictement décroissante sur
est strictement décroissante sur ![]() .
.
![]() et
et ![]()
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
![]()
![]() .
.
Question 2
Soit ![]() une suite de réels telle que
une suite de réels telle que
![]() .
.
Montrer que ![]() .
.
Correction de la question 2 :
La suite ![]() est une suite de réels strictement positifs à partir d’un certain rang
est une suite de réels strictement positifs à partir d’un certain rang ![]() car elle est équivalente à une suite à valeurs strictement positives.
car elle est équivalente à une suite à valeurs strictement positives.
![]()
alors ![]() admet
admet ![]() pour limite car la suite
pour limite car la suite ![]() converge vers 0 et en utilisant la continuité de
converge vers 0 et en utilisant la continuité de ![]()
![]()
![]()
ce qui donne ![]()
donc ![]() .
.
Question 3
Soit ![]() une suite de réels. Montrer que les deux propriétés suivantes sont équivalentes :
une suite de réels. Montrer que les deux propriétés suivantes sont équivalentes :
![]() 1)
1) ![]()
![]() 2)
2) ![]()
Correction de la question 3 :
![]() On suppose que
On suppose que ![]() ,
,
alors ![]() donc
donc
![]() donne
donne
![]()
![]()
![]()
![]()
et comme ![]()
on a prouvé que ![]()
![]() On suppose que
On suppose que ![]()
soit ![]()
par continuité de la fonction ![]() :
:
![]()
donc ![]()
et par division par ![]()
![]()
soit ![]() .
.
en utilisant la question 2 , ![]()
ou ![]()
puis par continuité de la fonction racine carrée et la positivité de ![]() ,
,
![]()
![]() .
.
On a établi l’équivalence des propriétés 1) et 2).
Exercice 3
On note ![]() .
.
Question 1
![]() admet une fonction réciproque
admet une fonction réciproque ![]() définie sur
définie sur ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction de l’exercice 3 :
![]() est continue sur
est continue sur ![]() , strictement croissante car
, strictement croissante car ![]() .
.
![]() ,
,![]()
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
Elle admet une fonction réciproque ![]() strictement croissante et définie sur
strictement croissante et définie sur ![]() .
.
3. Développement asymptotique d’une suite
On note si 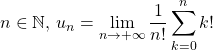
Question 1
La suite ![]() converge vers
converge vers
Correction de la question 1 :
On écrit ![]()
avec 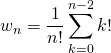
![]() est la somme de
est la somme de ![]() termes positifs et inférieurs à
termes positifs et inférieurs à ![]()
donc 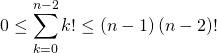
et ![]()
![]() ,
,
ce qui donne ![]() .
.
Question 2
![]()
Correction de la question 2 :
![]() donc
donc ![]()
avec 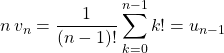
il suffit d’utiliser la question 1 avec ![]() :
:
![]()
![]() .
.
Question 3
Écrire un développement asymptotique en ![]() de
de ![]() .
.
Correction de la question 3 :
![]() On rappelle que
On rappelle que ![]()
et ![]()
On utilise le résultat de la question 2 avec ![]() .
.
à passer de l’expression en ![]() à une expression en
à une expression en ![]() !
!
On transforme l’expression en ![]()
et un expression en fonction de ![]() .
.
![]()
![]() donc
donc
![]()
![]()
![]()
donc ![]()
alors ![]()
donc ![]()
![]() On réitère le raisonnement :
On réitère le raisonnement :
![]()
![]()
![]()
![]() donc
donc
![]()
![]()
![]()
donc ![]()
![]()
![]()
![]()
![]() en conclusion
en conclusion
![]()
puis
![]()
On pourrait bien sûr pour suivre pour un développement asymptotique d’ordre plus élevé !
C’est une méthode classique.
Avis Google France ★★★★★ 4,9 sur 5COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
4. Développement asymptotique d’une suite implicite, exemple 1
Question 1
Montrer que pour tout ![]() , l’équation
, l’équation ![]() admet une unique solution réelle
admet une unique solution réelle ![]() .
.
Trouver ![]() .
.
Correction de la question 1 :
Soit ![]() est une fonction continue strictement croissante sur
est une fonction continue strictement croissante sur ![]() admettant
admettant ![]() pour limite en
pour limite en ![]() et
et
![]() pour limite en
pour limite en ![]() .
.
Donc ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
L’équation ![]() admet donc une unique solution
admet donc une unique solution ![]() .
.
Comme ![]() ,
,
alors ![]() .
.
Question 2
![]()
Correction de la question 2 :
![]() .
.
![]() On commence par déterminer
On commence par déterminer ![]() .
.
La relation de définition donne
![]()
avec ![]()
donc ![]()
et alors ![]() .
.
![]() On écrit la relation
On écrit la relation ![]() sous la forme :
sous la forme :
![]()
comme ![]()
![]() .
.
Alors ![]()
On a prouvé que : ![]()
Question 3
Trouver ![]() tel que
tel que
![]()
Correction de la question 3 :
![]() On avait trouvé
On avait trouvé
![]()
donc ![]()
avec ![]()
En utilisant ![]() ,
,
![]()
et par l’équivalent de la question précédente :
![]()
ce qui s’écrit
![]() .
.
5. Développement asymptotique d’une suite implicite, exercice 2
Question 1
Soit ![]() , montrer que l’équation
, montrer que l’équation ![]() admet une unique solution
admet une unique solution ![]() dans
dans ![]() .
.
Déterminer la limite de la suite ![]()
Correction de la question 1 :
![]()
![]() est continue sur
est continue sur ![]() , strictement croissante car
, strictement croissante car ![]() sur
sur ![]() , vérifie
, vérifie ![]() et
et
![]() .
.
Par le théorème de la bijection, il existe un unique ![]() tel que
tel que ![]() .
.
![]() Comme
Comme ![]() , par minoration,
, par minoration,
![]() .
.
Puis en divisant par ![]() ,
,
![]() .
.
Par encadrement ![]()
ce qui se traduit par ![]() .
.
Question 2
Montrer que la suite ![]() converge et déterminer sa limite.
converge et déterminer sa limite.
Correction de la question 2 :
On écrit la relation ![]() sous la forme
sous la forme ![]()
puis ![]()
avec ![]() , ce qui permet de simplifier :
, ce qui permet de simplifier : ![]()
donc ![]()
car ![]() .
.
Question 3
Trouver un développement asymptotique de ![]() en
en ![]() de
de ![]() .
.
Correction de la question 3 :
![]()
![]() .
.
On peut écrire puisque ![]() ,
,
![]()
![]() .
.
![]() On note
On note ![]() .
.
![]() .
.
En utilisant ![]() ,
,
![]()
ce qui permet d’écrire que
![]() .
.
![]() On réitère le raisonnement en écrivant
On réitère le raisonnement en écrivant
![]()
donc ![]()
avec ![]()
de limite nulle.
![]()
![]()
![]()
![]()
![]()
![]()
Puis comme ![]() ,
,
![]()
![]()
![]()
![]()
et
![]()
![]() .
.
6. Sur le DL de la fonction th en MPSI, PCSI, PTSI et MP2I
On rappelle que ![]() .
.
Question 1
Justifier que l’on peut écrire 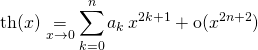
Correction de la question 1 :
La fonction th est de classe ![]() sur
sur ![]() et impaire, elle admet donc un DL à tout ordre en
et impaire, elle admet donc un DL à tout ordre en ![]() ne contenant que des puissances impaires.
ne contenant que des puissances impaires.
Question 2
En utilisant ![]() , exprimer si
, exprimer si ![]() ,
, ![]() en fonction des
en fonction des ![]() et de factorielles.
et de factorielles.
Correction de la question 2 :
On note 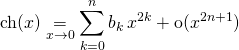
avec ![]()
Et on rappelle que 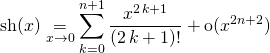
Par produit de deux DL à l’ordre ![]() dont l’un ne continent que des puissances paires et l’autre des puissances impaires, on obtient un DL ne contenant que des puissances impaires :
dont l’un ne continent que des puissances paires et l’autre des puissances impaires, on obtient un DL ne contenant que des puissances impaires :
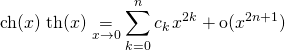 avec
avec ![]()
donc ![]()
puis en posant ![]() ,
,
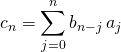
et par unicité du DL,
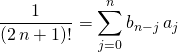
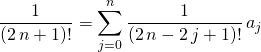
donc
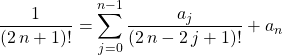
ce qui donne 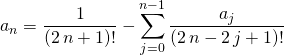
Question 3
En utilisant une équation différentielle d’ordre 1 vérifiée par th, trouver une autre expression de ![]() en fonction des
en fonction des ![]() .
.
Correction de la question 3 :
Pour tout réel ![]() ,
, ![]() si l’on note
si l’on note ![]() .
.
On rappelle que 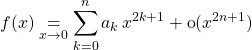
Comme la fonction ![]() est de classe
est de classe ![]() , on obtient le DL de
, on obtient le DL de ![]() à l’ordre
à l’ordre ![]() en dérivant le DL de
en dérivant le DL de ![]()
écrit à l’ordre ![]()
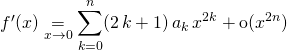
Puis on écrit le D de ![]() à l’ordre
à l’ordre ![]() en faisant le produit de deux DL écrits à l’ordre
en faisant le produit de deux DL écrits à l’ordre ![]() , le résultat ne contient que des puissances paires :
, le résultat ne contient que des puissances paires :
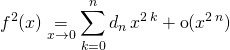
avec si ![]() ,
, ![]()
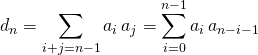
En égalant si ![]() les coefficients de
les coefficients de ![]() dans l’écriture des DL de la relation
dans l’écriture des DL de la relation ![]() ,
,
on obtient 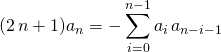
donc 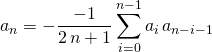 .
.
N’hésitez pas à utiliser les nombreux cours en ligne de Maths en Maths Sup mis à votre disposition pour maximiser vos résultats et améliorer vos méthodes de résolution d’exercices. Débutez dès maintenant les révisions pour les chapitres à venir :

