Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Espaces vectoriels exercices et corrigés en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
S’entraîner sur des exercices ou sur des annales des concours des écoles d’ingénieurs est le meilleur moyen de réviser efficacement, mais aussi de se rendre compte de son niveau, de ses points forts et de ses axes d’amélioration. Les entraînements sur des cas concrets sont indispensables pour intégrer les meilleures écoles d’ingénieurs françaises.
Exercice sur les familles libres et liées en Maths Sup
Dans ![]() , les familles suivantes forment-elles une famille libre ou liée ?
, les familles suivantes forment-elles une famille libre ou liée ?
Si elles forment une famille liée, donner une relation entre les applications.
Question 1 :
![]() ,
, ![]() ,
, ![]() .
.
Question 2 :
![]() ,
, ![]() et
et ![]() .
.
Question 3 :
Soient ![]() et
et ![]() trois réels deux à deux distincts modulo
trois réels deux à deux distincts modulo ![]() .
.
![]() ,
, ![]()
et ![]()
Question 4 :
Si ![]() sont réels et non nuls,
sont réels et non nuls,
![]()
![]()
![]()
Exercice sur les bases de sous-espaces vectoriels en Maths Sup
Question 1 :
Déterminer une base de ![]() .
.
![]() ?
?
Question 2 :
Donner une équation de ![]() dans la base canonique.
dans la base canonique.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice sur l’application linéaire d’un espace vectoriel
Soit ![]() .
.
Question 1 :
L’application définie sur ![]() par
par ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
Question 2 :
Déterminer une base de l’image et du noyau de ![]() .
.
Exercice sur l’existence d’un endomorphisme
Soit ![]() un espace vectoriel de dimension finie et
un espace vectoriel de dimension finie et ![]() et
et ![]() deux sous-espaces vectoriels de
deux sous-espaces vectoriels de ![]() .
.
Donner une CNS pour qu’il existe un endomorphisme ![]() de
de ![]() tel que
tel que ![]() et
et ![]() .
.
Exercice sur le théorème du rang d’un espace vectoriel
Soient ![]() et
et ![]() deux
deux ![]() -e.v. de dimension finie et
-e.v. de dimension finie et ![]() .
.
Montrer que les 3 propriétés suivantes sont équivalentes
a) ![]()
b) ![]()
c) ![]() et
et ![]() .
.
Correction de l’exercice sur les familles libres et liées
Question 1 :
Soient ![]() tels que
tels que ![]() .
.
![]() ,
, ![]()
pour ![]() ,
, ![]()
pour ![]() ,
, ![]() donc
donc ![]() .
.
avec ![]() ,
, ![]() .
.
Donc la famille est libre.
Question 2 :
C’est une famille liée car ![]() soit
soit ![]() .
.
Question 3 :
C’est une famille liée car ![]() et
et ![]() sont combinaisons linéaires de la famille
sont combinaisons linéaires de la famille ![]() et
et ![]() .
.
On écrit ![]() et
et ![]() donc
donc
![]()
![]()
soit ![]()
et ![]()
![]()
soit ![]()
On termine avec ![]() donc
donc
![]()
![]()
en réordonnant et avec un peu de trigonométrie
![]() .
.
Question 4 :
Soient ![]() et
et ![]() trois réels tels que
trois réels tels que ![]() .
.
![]()
![]()
![]() Si
Si ![]() , on obtient pour tout réel
, on obtient pour tout réel ![]() ,
,
![]()
en prenant la valeur en ![]() , en
, en ![]() , en
, en ![]() , on obtient
, on obtient
![]() ,
, ![]() et
et ![]() donc
donc ![]() .
.
La famille est libre.
![]() Si
Si ![]() , on obtient pour tout réel
, on obtient pour tout réel ![]() ,
,
![]()
donc
![]()
La fonction ![]() est bornée.
est bornée.
On passe à la limite lorsque ![]() si
si ![]() et
et ![]() si
si ![]() , comme
, comme ![]() admet une limite nulle, on obtient en passant à la limite,
admet une limite nulle, on obtient en passant à la limite, ![]() .
.
Il reste alors ![]()
![]() .
.
En évaluant en ![]() puis en
puis en ![]() on obtient
on obtient ![]() puis
puis ![]() .
.
La famille ![]() est libre.
est libre.
Correction sur les bases de sous-espaces vectoriels
Question 1 :
En utilisant la question précédente,
![]() est un vecteur
est un vecteur ![]() non nul de
non nul de ![]() .
.
Par la formule de Grassmann, ![]()
![]() ,
,
on obtient ![]() , alors
, alors ![]() est une base de la droite
est une base de la droite ![]() .
.
Question 2 :
![]() est un hyperplan de
est un hyperplan de ![]() , donc il admet une équation de la forme
, donc il admet une équation de la forme ![]() .
.
On rappelle qu’une base de ![]() est donnée par
est donnée par ![]() ,
, ![]() et
et ![]() .
.
En écrivant que ces trois vecteurs vérifient l’équation de l’hyperplan, on obtient le système
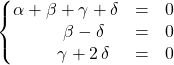
ssi 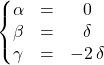
![]() a pour équation
a pour équation ![]() dans la base canonique.
dans la base canonique.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice sur l’application linéaire en Maths Sup
Question 1 :
![]() Si
Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
![]() Si
Si ![]() , comme
, comme ![]() est un polynôme de degré inférieur ou égal à 3,
est un polynôme de degré inférieur ou égal à 3, ![]() .
.
Donc ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
Question 2 :
![]() . On détermine les images des vecteurs de la base canonique.
. On détermine les images des vecteurs de la base canonique.
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() Il est évident que
Il est évident que
![]()
![]()
![]()
![]()
![]()
donc ![]() car la famille
car la famille ![]() est une famille de
est une famille de ![]() polynômes de degrés 2 à 2 distincts,
polynômes de degrés 2 à 2 distincts,
On a donc prouvé que ![]() est une base de
est une base de ![]()
![]() Par le théorème du rang,
Par le théorème du rang, ![]() et on a trouvé un élément non nul de
et on a trouvé un élément non nul de ![]() , donc une base du noyau est
, donc une base du noyau est ![]()
Correction de l’exercice sur l’existence d’endomorphisme en Maths Sup
a) S’il existe ![]() tel que
tel que ![]() et
et ![]() ,
,
par le théorème du rang, ![]() ,
,
donc ![]() .
.
b) On étudie la réciproque.
On suppose que ![]() .
.
![]() Première méthode : application du théorème de recollement des applications linéaires.
Première méthode : application du théorème de recollement des applications linéaires.
![]() On note
On note ![]() l’application linéaire nulle de
l’application linéaire nulle de ![]() dans
dans ![]() .
.
Soit ![]() un supplémentaire de
un supplémentaire de ![]() .
.
![]() .
.
Il existe donc un isomorphisme ![]() de
de ![]() sur
sur ![]() .
.
On note ![]() l’endomorphisme de
l’endomorphisme de ![]() obtenu par recollement des applications linéaires
obtenu par recollement des applications linéaires ![]() et
et ![]() .
.
i.e. si ![]() est écrit
est écrit ![]() avec
avec ![]() et
et ![]() , on définit
, on définit ![]() .
.
![]() Il est alors évident que
Il est alors évident que ![]() et que
et que ![]() .
.
![]() L’hypothèse et le théorème du rang donnent :
L’hypothèse et le théorème du rang donnent :
![]()
![]() .
.
Comme somme nulle de deux entiers naturels, ![]() et
et ![]() .
.
Par inclusion et égalité des dimensions, on a prouvé que
![]() et
et ![]() .
.
![]() Deuxième méthode : application du théorème de caractérisation des applications linéaires.
Deuxième méthode : application du théorème de caractérisation des applications linéaires.
![]() Si
Si ![]() , alors
, alors ![]() et
et ![]() , l’application
, l’application ![]() convient.
convient.
![]() Si
Si ![]() , alors
, alors ![]() et
et ![]() , l’application nulle convient.
, l’application nulle convient.
![]() Si
Si ![]() , on note
, on note ![]() et
et ![]() .
.
On introduit une base ![]() de
de ![]() et une base
et une base ![]() de
de ![]() .
.
Par le théorème de la base incomplète, on peut déterminer une base ![]() de
de ![]() .
.
On note ![]() l’unique endomorphisme de
l’unique endomorphisme de ![]() tel que
tel que
si ![]()
et si ![]() .
.
Il est alors évident que ![]() et que
et que ![]() .
.
On termine comme dans la première méthode.
Correction de l’exercice sur le théorème du rang
![]() On suppose que
On suppose que ![]() .
.
Comme ![]() ,
,
![]()
![]() .
.
On en déduit que ![]() .
.
Alors ![]() .
.
On peut donc écrire ![]() .
.
Alors ![]()
![]()
et ![]() donnent
donnent ![]() .
.
![]() On suppose que
On suppose que ![]() .
.
On en déduit que ![]() .
.
![]()
![]()
![]()
En appliquant la relation (*) et plusieurs fois la formule du rang,
![]()
![]()
![]() .
.
![]()
Ce que l’on écrit sous la forme (**)
![]()
![]() .
.
L’inclusion simple à justifier
![]()
donne ![]()
et en utilisant (**) :
![]() .
.
![]()
car ![]() est un sev de
est un sev de ![]() .
.
On a prouvé que ![]() .
.
![]()
![]() et (*)
et (*)
![]() .
.
![]()
![]()
![]()
et en utilisant ![]() et la formule de Grassmann,
et la formule de Grassmann,
![]() .
.
Comme ![]() est une inclusion toujours vérifiée, on a prouvé que
est une inclusion toujours vérifiée, on a prouvé que ![]() .
.
![]() On suppose que
On suppose que ![]() et
et ![]() .
.
![]() En utilisant
En utilisant ![]()
![]()
![]()
![]() En utilisant
En utilisant ![]() ,
,
![]()
![]()
en utilisant ![]() ,
,
![]()
soit ![]() .
.
On a prouvé l’équivalence des trois propriétés.
Pendant leur année de Maths Sup, les étudiants ont la possibilité de se faire accompagner pour améliorer leur moyenne et maximiser leurs chances de réussite aux concours, grâce à des cours particuliers ou stages intensifs en Maths Sup. En dehors de ces accompagnement, les étudiants peuvent aussi utiliser les cours en ligne pour s’entraîner sur divers chapitres du programme dont :

