Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Intégration en Maths Sup : exercices et corrigés
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Que ce soient les meilleures écoles du classement des écoles d’ingénieurs ou les autres écoles moins réputées, toutes accordent une très grande importance à la maîtrise des maths. C’est pourquoi les maths ont un coefficient en MP, PC, PSI et PT très élevé. Ces exercices vous permettent de pouvoir faire une bonne séance de révison sur l’intégration en Maths Sup.
Exercice sur les sommes de Riemann en Maths Sup
Soit ![]() une fonction de classe
une fonction de classe ![]() sur
sur ![]() à valeurs dans
à valeurs dans ![]() .
.
Déterminer ![]() où
où 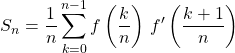
Exercices sur les limites de suites d’intégrales en Maths Sup
Exercice 1 sur les limites de suites d’intégrales :
Si ![]() , on note
, on note ![]() .
.
Question 1
Calculer ![]() et
et ![]() .
.
Question 2
Étudier le sens de la variation de la suite ![]() .
.
La suite ![]() est convergente.
est convergente.
Vrai ou Faux ?
Question 3
Écrire pour tout ![]() ,
, ![]() sous la forme d’une intégrale.
sous la forme d’une intégrale.
La suite ![]() converge vers
converge vers ![]() .
.
Vrai ou Faux ?
Question 4
Si ![]() ,
, ![]() et
et ![]() , on note
, on note ![]() .
.
Montrer que la fonction ![]() admet une limite que l’on notera
admet une limite que l’on notera ![]() lorsque
lorsque ![]() tend vers
tend vers ![]() .
.
La suite ![]() converge vers 0.
converge vers 0.
Vrai ou Faux ?
Exercice 2 sur les limites de suites d’intégrales :
![]() est définie si
est définie si ![]() et la suite
et la suite ![]() converge vers
converge vers ![]() .
.
Vrai ou Faux ?
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice sur une fonction définie par une intégrale en Maths Sup
Soit ![]() une fonction continue sur
une fonction continue sur ![]() . On pose pour
. On pose pour ![]() ,
, ![]()
Question 1 :
Si ![]() est dérivable en 0, montrer que
est dérivable en 0, montrer que ![]() est dérivable en
est dérivable en ![]() et donner la valeur de
et donner la valeur de ![]() .
.
Montrer que ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Question 2 :
Si ![]() , montrer que
, montrer que ![]() vérifie la même propriété.
vérifie la même propriété.
Que se passe-t-il si ![]() ?
?
Exercice sur les intégrales de Wallis
Question 1 :
![]()
avec ![]() ?
?
Question 2 :
![]() .
.
Vrai ou Faux ?
Question 3 :
Valeur de ![]()
Exercice sur l’application du lemme de Lebesgue
Question 1 :
Calculer ![]() et
et ![]() pour
pour ![]() .
.
Question 2 :
Montrer que ![]() .
.
En déduire la limite de la suite de terme général 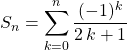 .
.
Question 3 :
Montrer que la fonction ![]()
est prolongeable par continuité en une fonction de classe ![]() sur
sur ![]() .
.
Correction de l’exercice sur les sommes de Riemann
Soit 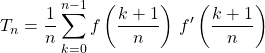 .
.
En posant ![]() ,
, 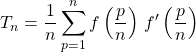 .
.
![]() est une somme de Riemann associée à la fonction continue
est une somme de Riemann associée à la fonction continue ![]() , donc
, donc
![]()
![]() .
.
![]()
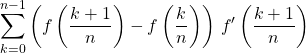
On introduit ![]() .
.
Par application de l’inégalité des accroissements finis,
![]()
et ![]()
donc 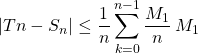
soit ![]() ,
,
ce qui donne ![]()
et ![]() .
.
Correction des exercices sur les limites de suites d’intégrales
Correction de l’exercice 1 sur les limites de suites d’intégrales :
Question 1 :
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
Question 2 :
Vrai,
![]()
![]()
![]()
![]()
Par intégration d’une fonction à valeurs positives ou nulles sur ![]() ,
, ![]() donc la suite
donc la suite ![]() est croissante.
est croissante.
![]() On remarque que
On remarque que ![]()
donc ![]()
soit ![]() .
.
La suite est croissante et majorée. Elle est convergente.
Question 3 :
Vrai
![]()
![]()
![]()
donc ![]()
car ![]()
donc ![]() ce qui donne par encadrement que la suite
ce qui donne par encadrement que la suite ![]() converge vers
converge vers ![]() .
.
Question 4 :
Vrai
![]() La fonction
La fonction ![]() est croissante sur
est croissante sur ![]() . Elle admet une limite finie ou infinie en
. Elle admet une limite finie ou infinie en ![]() .
.
On suppose ![]() ,
, ![]()
soit ![]()
![]()
![]() est majorée par
est majorée par ![]() .
.
Elle admet une limite finie ![]() lorsque
lorsque ![]() .
.
![]() On a obtenu
On a obtenu ![]()
donc pour tout ![]() .
.
Par encadrement, on en déduit que la suite ![]() converge vers 0.
converge vers 0.
Correction de l’exercice 2 sur les limites de suites d’intégrales :
Vrai
![]() ,
, ![]() est continue sur
est continue sur ![]() (utilisation d’un prolongement par continuité en
(utilisation d’un prolongement par continuité en ![]() ) donc
) donc ![]() est définie si
est définie si ![]() .
.
![]() est continue sur
est continue sur ![]() donc bornée, soit
donc bornée, soit ![]() .
.
Si ![]() ,
, ![]() vérifie
vérifie
![]()
donc ![]()
soit ![]()
ce qui donne ![]() .
.
Correction de l’exercice sur une fonction définie par une intégrale
Question 1 :
![]()
![]() admet un DL d’ordre 1 au voisinage de
admet un DL d’ordre 1 au voisinage de ![]() donné par
donné par
![]()
donc ![]() admet un DL d’ordre 2
admet un DL d’ordre 2
![]()
On obtient celui de ![]() à l’ordre 3
à l’ordre 3
![]()
et enfin
![]()
Comme ![]() admet un DL d’ordre 1 au voisinage de
admet un DL d’ordre 1 au voisinage de ![]() ,
, ![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
![]() On avait vu que pour
On avait vu que pour ![]() ,
, ![]()
en utilisant les DL de ![]() et
et ![]() écrits à l’ordre 1 :
écrits à l’ordre 1 :
![]()
![]()
![]()
ce qui donne ![]() .
.
![]() est continue en
est continue en ![]() .
.
On a prouvé que ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Question 2 :
![]() Cas d’une limite nulle. On traduit la limite :
Cas d’une limite nulle. On traduit la limite :
![]() si
si ![]() ,
, ![]() .
.
On suppose que ![]()
![]()
![]()
![]()
On introduit ![]()
donc ![]()
![]()
Ensuite ![]() .
.
Comme ![]() ,
,
![]()
![]()
puis si ![]() .
.
On a prouvé que ![]()
![]() Cas général, on pose
Cas général, on pose ![]() ,
, ![]() admet
admet ![]() pour limite en
pour limite en ![]()
et ![]() vérifie
vérifie
![]()
soit ![]() .
.
On en déduit que ![]() .
.
Correction de l’exercice sur les intégrales de Wallis en Maths Sup
Question 1 :
![]()
En intégrant ![]() par parties avec les fonctions de classe
par parties avec les fonctions de classe ![]() sur
sur ![]() :
:
![]() et
et ![]()
![]()
et ![]() .
.
![]()
![]() .
.
En utilisant ![]() , on obtient par linéarité de l’intégrale
, on obtient par linéarité de l’intégrale ![]() .
.
donc ![]() .
.
Question 2 :
Vrai
Comme la suite de terme général ![]() converge vers
converge vers ![]() ,
, ![]()
et comme ![]() ,
,
on a : ![]() .
.
Comme ![]() , on obtient l’équivalent énoncé.
, on obtient l’équivalent énoncé.
Question 3 :
On utilise ![]()
et ![]()
pour obtenir
![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice sur l’application du lemme de Lebesgue
Question 1 :
Soit ![]() .
.
![]() Comme
Comme ![]()
![]() , donc
, donc
![]() .
.
![]() Comme
Comme ![]()
![]() ,
,
donc par sommation et télescopage sachant que ![]() :
:
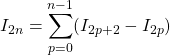
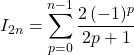 .
.
Question 2 :
![]()
![]()
![]() .
.
Avec un peu de trigonométrie,
![]()
![]()
et ![]()
![]()
![]()
On a donc écrit ![]()
où ![]() est une fonction de classe
est une fonction de classe ![]() sur
sur ![]() .
.
Par le lemme de Lebesgue,
![]() .
.
![]() donc
donc 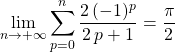
soit 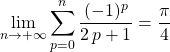 .
.
Question 3 :
![]()
![]() est continue sur
est continue sur ![]() .
.
![]() .
.
![]() et
et ![]()
![]() ,
,
on prolonge ![]() par continuité en 0 en posant
par continuité en 0 en posant ![]() .
.
![]()
![]() est de classe
est de classe ![]() sur
sur ![]() et
et
![]()
![]()
Comme ![]() , on écrit le développement limité de
, on écrit le développement limité de ![]() à l’ordre 4 en
à l’ordre 4 en ![]() .
.
![]()
et ![]()
donc ![]() .
.
![]() est continue sur
est continue sur ![]() , de classe
, de classe ![]() sur
sur ![]() et
et ![]() admet
admet ![]() pour limite en
pour limite en ![]() , donc par le théorème de la limite de la dérivée,
, donc par le théorème de la limite de la dérivée, ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]() .
.
Attention à commencer par réduire au même dénominateur pour lever l’indétermination ![]() .
.
Pour lever une indétermination en 0 de la forme ![]() par utilisation de développements limités, c’est l’ordre
par utilisation de développements limités, c’est l’ordre ![]() de l’équivalent du dénominateur qui impose d’écrire le DL du numérateur à l’ordre
de l’équivalent du dénominateur qui impose d’écrire le DL du numérateur à l’ordre ![]() .
.
On a utilisé la forme plus élaborée du théorème de la limite de la dérivée.
Si ![]() est une fonction réelle continue sur
est une fonction réelle continue sur ![]() , de classe
, de classe ![]() sur
sur ![]() et telle que
et telle que ![]() admet une limite finie
admet une limite finie ![]() en
en ![]() , alors
, alors ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]() .
.
Ces quelques exercices sont un bon entrainement pour constater une vraie progression en maths et réussir en Maths Sup. Réviser et s’entraîner régulièrement sur divers exercices de maths est la clé de la réussite. Voici quelques autres chapitres au programme à travailler :

