Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Les Polynômes en Maths Sup : Exercices corrigés
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Racines, Polynomes
1. Racines et décompositions
2. Division euclidienne
3. Racines multiples
4. Décomposition de polynômes
5. Polynômes vérifiant une condition
6. Polynômes scindés
7. Polynômes et limite de suites
8. Fonction ![]()
9. Divers
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Racines et factorisations
Exercice 1
Soit ![Rendered by QuickLaTeX.com P = \displaystyle \prod _{k = 1} ^n \left ( \textrm{X} - r_k \right) \in \mathbb{K}[\textrm{X}]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-579d0bc41a42883318373b838a103ca5_l3.png) .
.
Il existe ![]() tel que
tel que ![]()
Quelles sont les racines de ![]() ?
?
Correction :
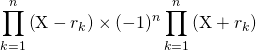
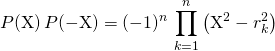
Donc
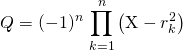
a pour racines
Exercice 2
Trouver les racines de ![]() sachant que le produit de deux d’entre elles vaut 6.
sachant que le produit de deux d’entre elles vaut 6.
Correction :
On note ![]() et
et ![]() les racines de
les racines de ![]() dans
dans ![]() . On sait que
. On sait que ![]() et que
et que ![]() , donc
, donc ![]() .
.
On écrit
![]()
![]()
![]()
on obtient les CNS :
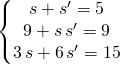
ssi ![]() ssi
ssi ![]() et
et ![]() .
.
![]()
![]() .
.
Exercice 3
Factoriser, dans ![]() le polynôme
le polynôme ![]() , sans chercher les racines de
, sans chercher les racines de ![]() .
.
Correction : La factorisation repose sur la relation fondamentale vérifiée dans ![]() :
: ![]() .
.
On obtient une première factorisation de ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
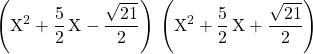
![]()
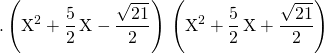
Exercice 4
Soit ![]()
Question 1
Pour tout ![]() divise
divise ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : Si ![]() ,
,
![]() avec
avec
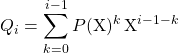 .
.
Pour ![]() , on écrit
, on écrit ![]() avec
avec ![]() .
.
Exercice 4 (fin)
Question 2
![]() est divisible par
est divisible par ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : On note ![]() , donc
, donc ![]()
et
![]()
en utilisant la question précédente
![]()
Donc ![]() est divisible par
est divisible par ![]() .
.
Exercice 5
Si ![]() , on note
, on note 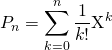
Question 1.
Les racines de ![]() sont simples. Vrai ou faux ?
sont simples. Vrai ou faux ?
Correction : Soit ![]() . On remarque que
. On remarque que
![]() et
et
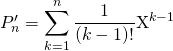
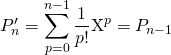 .
.
Si ![]() avait une racine multiple
avait une racine multiple ![]() , alors
, alors ![]() .
.
Donc ![]()
Comme ![]() , on aboutit à une contradiction.
, on aboutit à une contradiction.
Les racines de ![]() sont simples.
sont simples.
Exercice 5 (fin)
Question 2
Déterminer le nombre de racines réelles de ![]() .
.
Correction : Il est évident que si ![]() ,
,![]() .
.
![]() n’a pas de racine sur
n’a pas de racine sur ![]() .
.
Si ![]() ,
, ![]() :
: ![]() et
et ![]() s’annule une seule fois sur
s’annule une seule fois sur ![]() .
.
![]()
![]() et
et ![]() donc
donc ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vérifiée.
est vérifiée.
![]() Comme
Comme ![]() et
et ![]() s’annule en une seule fois en
s’annule en une seule fois en ![]() .
.
![]() et
et ![]() .
.
Comme deux fonctions équivalentes en ![]() ont même signe au voisinage de
ont même signe au voisinage de ![]() , on en déduit que si
, on en déduit que si ![]() et
et ![]() si
si ![]() .
.
![]() est une fonction strictement décroissante sur
est une fonction strictement décroissante sur ![]() et strictement croissante sur
et strictement croissante sur ![]() .
.
![]()
![]() , donc si
, donc si ![]() .
.
![]()
![]() , donc
, donc ![]() est une fonction strictement croissante sur
est une fonction strictement croissante sur ![]() telle que
telle que ![]() et
et ![]() ,
, ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() , donc
, donc ![]() s’annule une seule fois sur
s’annule une seule fois sur ![]() .
.
Ce qui prouve ![]() .
.
La propriété est démontrée par récurrence.
Exercice 7
Soit ![]() un polynôme de degré
un polynôme de degré ![]() ayant
ayant ![]() racines distinctes réelles. Montrer que
racines distinctes réelles. Montrer que ![]() n’a pas deux coefficients consécutifs nuls, autrement dit :
n’a pas deux coefficients consécutifs nuls, autrement dit : ![]() .
.
2. Division euclidienne
Exercice 1
Soit ![]() et
et ![]() .
.
On pose ![]() . Déterminer le reste de la division euclidienne de
. Déterminer le reste de la division euclidienne de ![]() par
par ![]() puis par
puis par ![]() .
.
Correction : ![]() Première question
Première question
D’après le théorème de division euclidienne, il existe ![]() et deux réels
et deux réels ![]() et
et ![]() tels que
tels que ![]() .
.
En particulier ![]()
or ![]()
![]()
en égalant parties réelles et parties imaginaires : ![]() et
et ![]() .
.
Le reste est égal à ![]() .
.
![]() Deuxième question
Deuxième question
D’après le théorème de division euclidienne, il existe ![]() tels que
tels que ![]() et
et ![]() .
.
![]() .
.
On traduit que ![]() est divisible par
est divisible par ![]() ce qui impose
ce qui impose
![]()
soit ![]()
ssi ![]()
et en égalant les parties réelles et imaginaires :
ssi 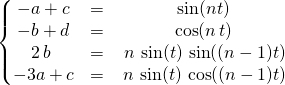
On obtient ![]()
![]()
![]()
![]()
Par ![]() :
:
![]()
![]()
![]()
![]()
![]()
Le reste est égal à
![]()
![]()
![]()
![]() .
.
Exercice 2 CENTRALE 2004-
Déterminer les polynômes ![]() tels que
tels que ![]() divise
divise ![]() .
.
Correction : ![]() Si
Si ![]() et
et ![]() divise
divise ![]() ssi
ssi ![]() .
.
![]() si
si ![]() , on écrit
, on écrit ![]() alors
alors ![]() , donc
, donc ![]() divise
divise ![]()
![]() Si
Si ![]() et si
et si ![]() divise
divise ![]() , il existe
, il existe ![]() tel que
tel que ![]()
en comparant les termes de plus haut degré, ![]() .
.
Par la formule de Leibniz avec les polynômes ![]() et
et ![]() sachant que
sachant que ![]() si
si ![]() ,
,
![]()
![]()
![]()
donc ![]() divise
divise ![]() avec
avec ![]() donc divise
donc divise ![]() .
.
On obtient donc : (*)
![]()
![]() divise
divise ![]() , qui divise
, qui divise ![]() , …. , qui divise
, …. , qui divise ![]() , qui divise
, qui divise ![]()
Comme ![]() , il existe
, il existe ![]() tel que
tel que ![]() soit la seule racine de
soit la seule racine de ![]() .
.
Par ![]() ,
, ![]() ,
, ![]() et bien sûr
et bien sûr ![]() .
.
![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]() .
.
On peut écrire ![]() avec
avec ![]() .
.
Réciproquement si ![]() avec
avec ![]() et
et ![]()
![]() divise
divise ![]() .
.
En remarquant que si ![]() , on peut aussi écrire
, on peut aussi écrire ![]() sous cette forme, et que le cas
sous cette forme, et que le cas ![]() est obtenu pour
est obtenu pour ![]()
![]() divise
divise ![]() ssi il existe
ssi il existe ![]() et
et ![]() tel que
tel que ![]() .
.
Exercice 3
Trouver tous les polynômes ![]() de degré inférieur ou égal à
de degré inférieur ou égal à ![]()
puis tous les polynômes tels que ![]() divise
divise ![]() et
et ![]() divise
divise ![]() .
.
Correction : Première question
![]()
![]() est un multiple de
est un multiple de ![]() ssi
ssi ![]()
ssi ![]() divise
divise ![]() et
et ![]() .
.
![]()
![]() est un multiple de
est un multiple de ![]() ssi
ssi ![]() et
et ![]()
ssi ![]() divise
divise ![]() et
et ![]() .
.
Comme ![]() ,
, ![]() divise
divise ![]() et
et ![]() , on en déduit qu’il existe
, on en déduit qu’il existe ![]()
![]()
ssi Il existe ![]() ,
, ![]() .
.
On termine en utilisant ![]()
ssi ![]()
et ![]()
ssi ![]() et
et ![]()
ssi ![]() et
et ![]() .
.
Le premier problème a une seule solution ![]() .
.
Deuxième partie
![]() Si
Si ![]() est solution et
est solution et ![]() le polynôme précédent,
le polynôme précédent, ![]() est divisible par
est divisible par ![]() et
et ![]() .
.
Soit il existe ![]() tel que
tel que ![]() .
.
![]() Réciproquement s’il existe
Réciproquement s’il existe ![]() tel que
tel que ![]() .
.
alors ![]() est divisible par
est divisible par ![]() .
.
De même ![]() est divisible par
est divisible par ![]() .
.
L’ensemble des solutions est l’ensemble des polynômes
![]() où
où ![]()
![]() et
et ![]() .
.
Exercice 4
Soit pour ![]() , le polynôme :
, le polynôme :
![]()
Question 1
Déterminer les racines de ![]() .
.
Question 2
Déterminer l’ensemble des ![]() tels que
tels que ![]() divise
divise ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Racines multiples
Exercice 1
Soient ![]() dans
dans ![]() et
et ![]() .
.
Soit ![]() .
.
Déterminer le reste de la division de ![]() par
par ![]() .
.
Correction : Par le théorème de division euclidienne, on peut trouver ![]() tels que
tels que ![]() et
et ![]() . .
. .
On traduit que ![]() divise
divise ![]() par les conditions :
par les conditions :
![]()
![]() .
.
![]() .
.
Donc ![]() est nul en
est nul en ![]() et
et ![]() , il est donc divisible par
, il est donc divisible par ![]() et de degré inférieur ou égal à 3.
et de degré inférieur ou égal à 3.
On écrit ![]()
![]()
![]()
![]()
![]()
donne ![]()
ssi ![]() (1)
(1)
![]()
donne ![]()
ssi ![]() (2)
(2)
On résout le système
![]()
ssi ![]() et
et ![]()
donc le reste est égal à ![]()
Exercice 2
Soient ![]() , sans racine commune.
, sans racine commune.
On suppose que ![]() est une racine multiple de
est une racine multiple de ![]() , alors
, alors ![]() est racine de
est racine de ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
On écrit ![]() avec
avec ![]() et
et ![]()
![]() ssi
ssi ![]() .
.
Si l’on avait ![]() , par somme et différence, on aurait
, par somme et différence, on aurait
![]() et
et ![]() ce qui est exclu par hypothèse.
ce qui est exclu par hypothèse.
Donc ![]() est racine d’un seul des deux polynômes
est racine d’un seul des deux polynômes ![]() ,
, ![]() .
.
On peut supposer (en remplaçant si nécessaire ![]() par
par ![]() ) que
) que ![]() et
et ![]() .
.
Puis comme ![]() est racine d’ordre au moins égal à 2 de
est racine d’ordre au moins égal à 2 de ![]()
![]() soit
soit ![]()
donc ![]() avec
avec ![]() alors
alors ![]() .
.
En utilisant ![]() , on a prouvé que
, on a prouvé que ![]() est racine de
est racine de ![]() .
.
4. Décomposition de polynômes
Exercice 1
Soit ![]() tel que
tel que ![]()
On dit que ![]() est positif si
est positif si ![]() .
.
Montrer que ![]() est positif ssi il existe deux polynômes
est positif ssi il existe deux polynômes ![]() et
et ![]() à coefficients dans
à coefficients dans ![]() n’ayant pas de racine réelle commune tels que
n’ayant pas de racine réelle commune tels que ![]() .
.
Correction : ![]() Condition suffisante
Condition suffisante
Si ![]() , où
, où ![]() ,
, ![]() et
et ![]() n’ont pas de racine réelle commune.
n’ont pas de racine réelle commune.
![]() car
car ![]() et
et ![]() sont réels.
sont réels.
Si ![]() ,
, ![]() (comme somme nulle de deux réels positifs ou nuls), ce qui est exclu lorsque
(comme somme nulle de deux réels positifs ou nuls), ce qui est exclu lorsque ![]() , donc pour tout réel
, donc pour tout réel ![]() .
.
![]() Condition nécessaire
Condition nécessaire
Si ![]() ,
, ![]() n’a que des racines complexes non réelles, elles sont deux à deux conjuguées (car
n’a que des racines complexes non réelles, elles sont deux à deux conjuguées (car ![]() est à coefficients réels) et deux racines conjuguées ont même ordre de multiplicité.
est à coefficients réels) et deux racines conjuguées ont même ordre de multiplicité.
La décomposition de ![]() dans
dans ![]() est donc de la forme
est donc de la forme 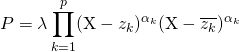 .
.
où ![]() .
.
On note ![]() , au voisinage de
, au voisinage de ![]() ,
, ![]() .
.
Si l’on avait ![]() , on aurait
, on aurait ![]() , donc pour
, donc pour ![]() assez grand,
assez grand, ![]() , ce qui est absurde. On en déduit que
, ce qui est absurde. On en déduit que ![]() .
.
On peut donc écrire ![]() , avec
, avec 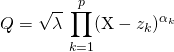 .
.
En introduisant la partie réelle et la partie imaginaire des coefficients de ![]() , on peut trouver
, on peut trouver ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() .
.
Alors ![]() et
et ![]() .
.
![]() et
et ![]() ne peuvent pas avoir une racine réelle commune
ne peuvent pas avoir une racine réelle commune ![]() , sinon P s’annulerait en
, sinon P s’annulerait en ![]() .
.
Il existe donc ![]() et
et ![]() à coefficients réels tels que
à coefficients réels tels que ![]() .
.
Exercice 2
Soit ![]() un entier strictement positif. On note
un entier strictement positif. On note ![]() où
où ![]()
Question 1
Décomposer ![]() dans
dans ![]() puis dans
puis dans ![]() .
.
Question 2
Si ![]() ,
, 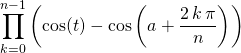
![]() .
.
Question 3
En déduire une expression simple de 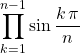 .
.
5. Polynômes vérifiant une condition
Exercice 1 ENSEA 2015
L’ensemble des polynômes ![]() de
de ![]() tels que
tels que ![]() est inclus dans
est inclus dans ![]() est l’ensemble des polynômes égaux à une constante réelle. Vrai ou Faux ?
est l’ensemble des polynômes égaux à une constante réelle. Vrai ou Faux ?
Correction : ![]() Si
Si ![]() ,
, ![]() est solution ssi
est solution ssi ![]()
![]() Si
Si ![]() , soit
, soit ![]() , le polynôme
, le polynôme ![]() est un polynôme de degré supérieur ou égal à 1, il admet au moins une racine dans
est un polynôme de degré supérieur ou égal à 1, il admet au moins une racine dans ![]() , donc il existe
, donc il existe ![]() tel que
tel que ![]() , donc
, donc ![]() n’est pas inclus dans
n’est pas inclus dans ![]()
Les seules solutions sont les polynômes constants et réels.
Exercice 2 Télécom Sud Paris 2014
Il y a au moins deux polynômes ![]() tels que
tels que ![]() et
et ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() On note
On note ![]() et si
et si ![]() .
.
On définit ainsi une suite strictement croissante car ![]() (le discriminant de
(le discriminant de ![]() est strictement négatif).
est strictement négatif).
![]() On démontre que pour tout
On démontre que pour tout ![]() ,
, ![]() .
.
La propriété est vraie pour ![]() .
.
Si elle est vraie au rang ![]() ,
, ![]()
![]() , elle est vraie pour tout
, elle est vraie pour tout ![]() .
.
![]() Le polynôme
Le polynôme ![]() s’annule une infinité de fois, donc
s’annule une infinité de fois, donc ![]() .
.
Il est évident que le polynôme ![]() vérifie les conditions.
vérifie les conditions.
Le problème admet une unique solutionle polynôme ![]() .
.
Exercice 3
Soit P un polynôme à coefficients réels de degré ![]() vérifiant :
vérifiant : ![]() .
.
Calculer ![]() puis
puis ![]() lorsque
lorsque ![]() .
.
Exercice 4
Soit ![]() ,vérifiant la contdition (*)
,vérifiant la contdition (*)
![]() .
.
Question 1
Déterminer les polynômes constants vérifiant (*).
Question 2.
On suppose que ![]() admet une racine
admet une racine ![]() , où
, où ![]() n’est pas un entier naturel. Montrer que
n’est pas un entier naturel. Montrer que ![]() est racine de
est racine de ![]() .
.
En déduire que toute racine ![]() de
de ![]() est élément de
est élément de ![]() .
.
Question 3
On suppose que ![]() est une racine de
est une racine de ![]() . Montrer que
. Montrer que ![]() est racine de
est racine de ![]() . En déduire une contradiction.
. En déduire une contradiction.
Question 4.
Déduire des calculs précédents, l’ensemble des polynômes vérifiant (*).
6. Polynômes scindés
Exercice 1 CCP 2013
Soit ![]() tel que
tel que ![]() et
et ![]() unitaire.
unitaire.
Question 1
Soit ![]() . Montrer que pour tout
. Montrer que pour tout ![]() ,
, ![]() .
.
Correction : On note ![]() avec
avec ![]() et
et ![]() réels et
réels et ![]() .
.
![]() , donc
, donc ![]() .
.
Question 2
Montrer que ![]() est scindé sur
est scindé sur ![]() ssi pour tout
ssi pour tout ![]() .
.
Correction : ![]() On suppose que
On suppose que ![]() est scindé sur
est scindé sur ![]() , il existe donc
, il existe donc ![]() dans
dans ![]() tels que pour tout
tels que pour tout 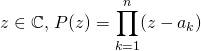 .
.
Alors 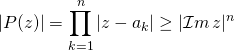 .
.
![]() On suppose que
On suppose que ![]() .
.
Soit ![]() une racine complexe de
une racine complexe de ![]() .
.
Alors ![]() donc
donc ![]() .
.
Toutes les racines complexes de ![]() sont réelles, donc
sont réelles, donc ![]() qui est scindé sur
qui est scindé sur ![]() est en fait scindé sur
est en fait scindé sur ![]() .
.
Exercice 2 ARTS2015
Soit ![]() un polynôme de
un polynôme de ![]() scindé à racines réelles simples. On pose
scindé à racines réelles simples. On pose ![]() .
.
Montrer que ![]() est scindé à racines réelles simples.
est scindé à racines réelles simples.
Correction :
On note ![]() .
.
![]() 1er cas : on suppose que
1er cas : on suppose que ![]() n’est pas racine de
n’est pas racine de ![]() , donc le polynôme
, donc le polynôme ![]() admet
admet ![]() racines distinctes que l’on range par ordre strictement croissant sous la forme
racines distinctes que l’on range par ordre strictement croissant sous la forme ![]() .
.
On applique le théorème de Rolle à ![]() sur l’intervalle
sur l’intervalle ![]() où
où ![]() .
.
On en déduit qu’il existe ![]() tel que
tel que ![]() .
.
On a donc déterminé ![]() racines distinctes pour
racines distinctes pour ![]() . Comme
. Comme ![]() ,
, ![]() , le polynôme
, le polynôme ![]() est donc scindé à racines simples.
est donc scindé à racines simples.
![]() 2ème cas : on suppose que
2ème cas : on suppose que ![]() est racine de
est racine de ![]() . Le polynôme Q s’annule donc en
. Le polynôme Q s’annule donc en ![]() réels que l’on range sous forme strictement croissante
réels que l’on range sous forme strictement croissante
![]() et il existe
et il existe ![]() tel que
tel que ![]() .
.
On applique le théorème de Rolle à ![]() sur l’intervalle
sur l’intervalle ![]() où
où ![]() .
.
On en déduit qu’il existe ![]() tel que
tel que ![]() .
.
Puis comme ![]() est racine double de
est racine double de ![]() ,
, ![]() et
et ![]() pour tout
pour tout ![]() .
.
On a donc déterminé ![]() racines distinctes pour
racines distinctes pour ![]() . Comme
. Comme ![]() , le polynôme
, le polynôme ![]() est donc scindé à racines simples.
est donc scindé à racines simples.
Exercice 3 Centrale 2014 et 2018
Soient ![]() non constants. On suppose que
non constants. On suppose que ![]() et
et ![]() ont les mêmes racines
ont les mêmes racines ![]() avec pour ordres de multiplicités respectifs
avec pour ordres de multiplicités respectifs ![]() et
et ![]() dans
dans ![]() .
.
On suppose que les polynômes ![]() et
et ![]() ont les mêmes racines
ont les mêmes racines ![]() avec pour ordres de multiplicités respectifs
avec pour ordres de multiplicités respectifs ![]() et
et ![]() dans
dans ![]() .
.
Question 1
Montrer que pour tout ![]() ,
, ![]() est racine de
est racine de ![]() avec pour ordre de multiplicité
avec pour ordre de multiplicité ![]() .
.
Question 2
Montrer de même que pour tout ![]() ,
, ![]() est racine de
est racine de ![]() avec pour ordre de multiplicité
avec pour ordre de multiplicité ![]() .
.
Question 3
En déduire que ![]() .
.
Question 4
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
7. Polynômes et limite de suites
Soit ![]() un entier strictement positif. On note
un entier strictement positif. On note ![]() .
.
Question 1
Montrer que ![]() est un polynôme à coefficients réels. Préciser son degré et son coefficient dominant.
est un polynôme à coefficients réels. Préciser son degré et son coefficient dominant.
Correction : On utilise le binôme de Newton :
![]()
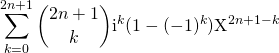
si ![]() ,
, ![]()
si ![]() ,
, ![]() et
et ![]()
On se limite aux indices ![]() avec
avec ![]() .
.
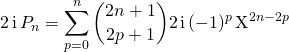
et après simplification par ![]()
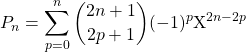
C’est un polynôme à coefficients réels, de degré ![]() , de coefficient dominant (obtenu pour
, de coefficient dominant (obtenu pour ![]() ) égal à
) égal à ![]() .
.
Question 2
Déterminer les racines de ![]() .
.
Correction : ![]()
![]() n’étant pas solution de cette équation, on peut écrire en posant
n’étant pas solution de cette équation, on peut écrire en posant ![]()
![]()
![]() ssi
ssi ![]()
ssi ![]()
On remarque qu’il est impossible d’avoir ![]() et qu’alors
et qu’alors ![]() .
.
Il reste à simplifier cette expression lorsque ![]() est une racine
est une racine ![]() -ème de
-ème de ![]() différente de
différente de ![]() soit lorsque
soit lorsque ![]() avec
avec ![]()
On note dans la suite ![]() .
.
Les racines de ![]() sont les complexes
sont les complexes
![]() .
.
En utilisant les résultats classiques ;
![]()
![]()
![]() .
.
![]() admet
admet ![]() racines
racines ![]() où
où ![]() .
.
Question 3
Montrer qu’il existe un polynôme ![]() à coefficients réels tel que
à coefficients réels tel que ![]() .
.
Correction : On a prouvé que 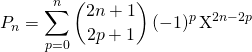
en posant 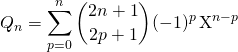 .
.
![]() est un polynôme à coefficients réels tels que
est un polynôme à coefficients réels tels que ![]() .
.
On rappelle que ![]() est un polynôme de degré
est un polynôme de degré ![]() de coefficient dominant égal à
de coefficient dominant égal à ![]() et dont les racines sont les complexes
et dont les racines sont les complexes ![]() :
:
donc ![]()
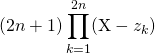
![]() où
où ![]()
![]()
![]()
On écrit
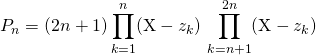
On pose ![]() dans
dans
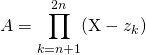
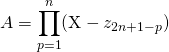
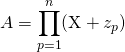
donc
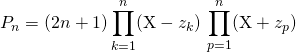
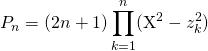
Puis comme ![]() ,
,
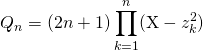
Les racines de ![]() sont
sont ![]() pour
pour ![]() .
.
Question 4
Calculer 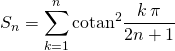
Correction : C’est la somme des racines du polynômes ![]() .
.
Le coefficient dominant de ![]() est
est ![]() .
.
Le coefficient ![]() de
de ![]() dans
dans ![]() donc celui de
donc celui de ![]() dans
dans ![]() .
.
Les calculs de la première question donnent : ![]()
![]()
![]() est la somme des
est la somme des ![]() racines de
racines de ![]()
![]() .
.
Question 5
On note ![]()
Montrer que ![]() .
.
Question 6
Soit 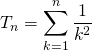
Montrer que la suite ![]() converge et déterminer sa limite.
converge et déterminer sa limite.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
8. Fonction 
Question 1
![]() et si
et si ![]()
![]()
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : La propriété est évidente si ![]() .
.
On suppose que ![]() .
.
![]() si
si ![]()
![]() si
si ![]() et
et ![]() .
.
![]()
![]()
![]() si
si ![]() .
.
On écrit ![]() avec
avec ![]()
![]()
![]()
![]()
La propriété a été prouvée par disjonction de cas.
Question 2
Soit si ![]()
![]() .
.
a) Quel est le degré de ![]() si
si ![]() ?
?
Correction : ![]()
![]() .
.
![]() Si
Si ![]() ,
,
![]()
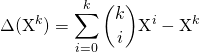
alors ![]() si
si ![]() .
.
Question 2
b) Calculer ![]() .
.
Question 3
Calculer si ![]() ,
, ![]() .
.
Question 4
Soit ![]() .
.
Il y a équivalence entre
1) ![]()
2) ![]() tel que
tel que 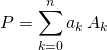 . Vrai ou Faux ?
. Vrai ou Faux ?
9. Divers
Exercice 1 MinesPonts 2015
Pour ![]() de degré
de degré ![]() écrit sous la forme
écrit sous la forme 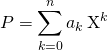 ,
,
montrer que ![]() avec
avec ![]() .
.
Exercice 2 Centrale PSI 2018
Question 1 Soit ![]() .
.
Si ![]() ,
, ![]() .
.
Question 2
Trouver ![]() contenant un coefficient strictement négatif et tel que
contenant un coefficient strictement négatif et tel que ![]() .
.
Question 3
On dit que ![]() est à valeurs positives lorsque
est à valeurs positives lorsque
![]() .
.
a) Soit ![]() à valeurs positives,
à valeurs positives,
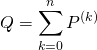 est à valeurs positives. Vrai ou Faux ?
est à valeurs positives. Vrai ou Faux ?
b) La réciproque est vraie
Plusieurs autres chapitres de Maths, comprenant des notions de cours, des méthodes et des exercices corrigés peuvent également être travaillés grâce à nos cours en ligne de maths pour les Maths Sup, comme par exemple :

