Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les séries numériques de Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
S’entraîner sur des exercices constitue un moyen efficace pour vérifier son niveau de connaissances. Avoir acquis l’ensemble des notions du programme de maths en MPSI, PCSI, PTSI est plus qu’essentiel pour les étudiants s’ils souhaitent réussir en Maths Spé et par conséquent, obtenir les meilleurs résultats qu’ils soient aux concours post-prépa.
Exercice sur les études de convergence de séries en Maths Sup
Question 1 :
Nature de ![]() si
si ![]()
Série convergente ou divergente ?
Question 2 :
Nature de ![]() si
si ![]()
Série convergente ou divergente ?
Question 3 :
Nature de ![]() si
si ![]()
Série convergente ou divergente ?
Question 4 :
Ensemble des réels ![]() et
et ![]() tels que si
tels que si
![]()
![]() ,
, ![]() soit convergente.
soit convergente.
Question 5 :
La série de terme général ![]() est convergente ou divergente ?
est convergente ou divergente ?
Question 6 :
Soient ![]() et
et ![]() deux réels strictement positifs et
deux réels strictement positifs et ![]() .
.
Nature de ![]() .
.
Exercices sur les calculs de sommes de séries en Maths Sup
Exercice 1 sur les calculs de sommes de séries :
La somme 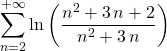 est définie et égale à
est définie et égale à ![]()
avec ![]() ?
?
Exercice 2 sur les calculs de sommes de séries en Maths Sup :
Question 1 :
![]() :
: ![]() ,
, ![]() est continue sur
est continue sur ![]() ].
].
Vrai ou Faux ?
Question 2 :
Montrer que la série de terme général ![]() converge et exprimer sa somme à l’aide d’une intégrale.
converge et exprimer sa somme à l’aide d’une intégrale.
Exercice sur la constante d’Euler et applications en Maths Sup
Il existe un réel ![]() (appelé constante d’Euler) tel que
(appelé constante d’Euler) tel que 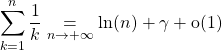 .
.
Exercice de suite décroissante de réels positifs & série convergente
Question 1 :
Si la suite ![]() est une suite décroissante de réels positifs ou nuls tels que la série de terme général
est une suite décroissante de réels positifs ou nuls tels que la série de terme général ![]() converge,
converge, 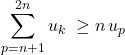 avec avec
avec avec ![]()
Sous les hypothèses de la question 1, la suite ![]() converge vers 0.
converge vers 0.
Vrai ou Faux ?
Question 2 :
Il existe une série de terme général ![]() à termes positifs ou nuls et convergente telle que la suite
à termes positifs ou nuls et convergente telle que la suite ![]() ne converge pas vers 0.
ne converge pas vers 0.
Vrai ou Faux ?
Exercice sur la relation simple entre  et
et  en Maths Sup
en Maths Sup
On suppose que ![]() et
et ![]() sont deux réels strictement positifs.
sont deux réels strictement positifs.
On définit une suite ![]() par
par ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
Question 1 :
La suite est bien définie et à valeurs strictement positives.
Vrai ou Faux ?
Question 2 :
a) Déterminer le réel ![]() tel que la série de terme général
tel que la série de terme général ![]() soit convergente.
soit convergente.
![]() ?
?
b) En déduire un équivalent de ![]() .
.
Donner une CNS pour que ![]() converge.
converge.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice sur les études de convergence de séries
Question 1 :
Série divergente.
Pour ![]() donc
donc ![]() .
.
Par minoration par une série de Riemann divergente, ![]() diverge.
diverge.
Question 2 :
Série convergente.
Si ![]()
et ![]() est une série géométrique convergente car
est une série géométrique convergente car ![]() .
.
Par majoration par une série convergente, la série à termes positifs ![]() converge. Il n’est pas toujours utile d’utiliser l’astuce du
converge. Il n’est pas toujours utile d’utiliser l’astuce du ![]() .
.
C’est en particulier maladroit en présence d’une série proportionnelle à une série géométrique ce qui est le cas pour ![]() lorsque
lorsque ![]() .
.
Question 3 :
Série divergente.
On étudie ![]() .
.
![]() .
.
Par utilisation de la quantité conjuguée,
![]()
![]()
Soit ![]() ,
, ![]() .
.
![]()
![]()
![]()
![]()
donc ![]()
et pour ![]() assez grand,
assez grand, ![]() donc
donc ![]() .
.
Par minoration par une série de Riemann divergente, la série à termes positifs ![]() diverge.
diverge.
Question 4 :
On écrit le développement limité de ![]() à l’ordre 2 en
à l’ordre 2 en ![]() en utilisant les DL usuels.
en utilisant les DL usuels.
![]()
![]()
![]()
![]()
![]() Si
Si ![]() ,
, ![]() diverge grossièrement.
diverge grossièrement.
![]() Si
Si ![]() et
et ![]() ,
, ![]() , par comparaison par équivalence à une série de Riemann de signe constant et divergente,
, par comparaison par équivalence à une série de Riemann de signe constant et divergente, ![]() diverge.
diverge.
![]() Si
Si ![]() ,
, ![]() , par comparaison par équivalence à une série de Riemann de signe constant et convergente,
, par comparaison par équivalence à une série de Riemann de signe constant et convergente, ![]() converge.
converge.
Question 5 :
Elle est convergente.
Par inégalité
Si ![]()
Par intégration, ![]() où
où ![]() .
.
![]() .
.
Comme ![]() ,
,
par comparaison suite -série, ![]() converge.
converge.
Donc par domination, ![]() converge.
converge.
Question 6 :
![]() Si
Si ![]() ,
, ![]() car
car
![]() où
où ![]() ,
,
donc ![]()
![]() Si
Si ![]() ,
, ![]() .
.
Par domination par une série géométrique convergente, ![]() converge et par équivalence de séries de réels positifs,
converge et par équivalence de séries de réels positifs, ![]() converge.
converge.
![]() Si
Si ![]() , alors
, alors ![]() , donc par minoration par une série de Riemann divergente,
, donc par minoration par une série de Riemann divergente,
![]() diverge et par équivalence de séries de réels positifs,
diverge et par équivalence de séries de réels positifs, ![]() diverge.
diverge.
![]() Si
Si ![]() ,
, ![]() car
car ![]() où
où
![]() (croissance comparée), donc
(croissance comparée), donc ![]() .
.
Par équivalence à une série géométrique positive, ![]() converge ssi
converge ssi ![]() .
.
En résumé , ![]() converge ssi
converge ssi
![]() (
(![]() et
et ![]() )
)
![]() ou (
ou (![]() et
et ![]() ).
).
Correction des exercices sur les calculs de sommes de séries
Correction de l’exercice 1 sur les calculs de sommes de séries en Maths Sup
avec ![]()
![]() Convergence
Convergence
On utilise ![]() ,
,
![]()
![]()
![]() .
.
Par équivalence d’une série de signe constant à une série de Riemann convergente, ![]() converge.
converge.
![]() Calcul de la somme
Calcul de la somme
![]()
![]()
![]() avec
avec ![]() où
où ![]() .
.
Comme 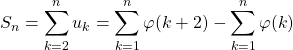
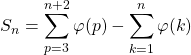
par télescopage,
![]()
Puis comme ![]() ,
,
![]() .
.
La somme ![]() de la série est égale à
de la série est égale à ![]() .
.
Correction de l’exercice 2 sur les calculs de sommes de séries :
Question 1 :
Vrai
![]() :
: ![]() est continue sur
est continue sur ![]() .
.
On utilise ![]() .
.
donc ![]() .
.
![]() admet
admet ![]() pour limite en
pour limite en ![]() , donc
, donc ![]() est continue en
est continue en ![]() .
.
Question 2 :
![]() est continue sur
est continue sur ![]() . On note
. On note ![]() un majorant de
un majorant de ![]() sur
sur ![]() .
.
Si ![]() ,
, 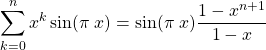
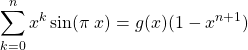 .
.
La relation reste vraie en ![]() , car elle s’écrit
, car elle s’écrit ![]() .
.
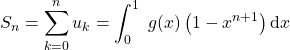
![]()
Soit ![]()
avec ![]() , donc
, donc 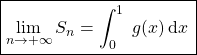 .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice sur la constante d’Euler et applications
On note ![]() la limite de la suite
la limite de la suite ![]() .
.
Donc ![]() ,
,
soit 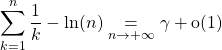
ce qui s’écrit :
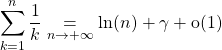 .
.
De la relation précédente, on déduit que 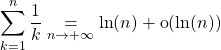
donc 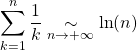 .
.
Correction de suite décroissante de réels positifs & série convergente
Question 1 :
Vrai
![]() Alors
Alors ![]()
Par encadrement par deux suites qui convergent vers 0, ![]()
![]() Puis si
Puis si ![]() ,
, ![]() , donc par encadrement,
, donc par encadrement, ![]() .
.
Par propriété des suites extraites, ![]() .
.
Question 2 :
Vrai
La suite de terme général ![]() ne converge pas vers 0, car la suite extraite
ne converge pas vers 0, car la suite extraite ![]() est une suite constante égale à 1.
est une suite constante égale à 1.
On a vu que la série de terme général ![]() converge.
converge.
Correction de l’exercice sur la relation simple entre  et
et 
Question 1 :
Vrai
Si ![]() , on note
, on note
![]() est défini et
est défini et ![]() .
.
![]() est vérifiée par hypothèse sur
est vérifiée par hypothèse sur ![]() .
.
On suppose que ![]() est vérifiée,
est vérifiée, ![]() est défini car
est défini car ![]() .
.
![]() et
et ![]() , donc
, donc ![]() est vérifiée.
est vérifiée.
Par récurrence, on a établi que ![]() pour tout
pour tout ![]() de
de ![]() .
.
Question 2 :
a) ![]()
DL de ![]() puis comparaison suite-série .
puis comparaison suite-série .
On étudie la convergence de la série de terme général ![]() .
.
![]()
![]()
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]() par équivalence à une série de Riemann de signe constant divergente,
par équivalence à une série de Riemann de signe constant divergente, ![]() diverge.
diverge.
![]() Si
Si ![]() ,
, ![]() , par domination par une série de Riemann divergente,
, par domination par une série de Riemann divergente, ![]() converge absolument.
converge absolument.
En conclusion, pour ![]() ,
, ![]() converge absolument.
converge absolument.
Le raisonnement avec « O » évite de calculer le développement limité à l’ordre 2 et abrège les calculs.
b) Par comparaison suite-série, la suite de terme général ![]() converge vers une limite
converge vers une limite ![]() , donc par continuité de la fonction exponentielle,
, donc par continuité de la fonction exponentielle,
![]()
donc ![]() .
.
On en déduit que ![]() converge ssi
converge ssi ![]() .
.
Participer à des stages intensifs de révision en Maths Sup est un moyen efficace pour progresser et faire grimper sa moyenne de maths rapidement. Cependant, entre deux périodes de stage, il ne faut pas relâcher ses efforts. Utiliser les cours en ligne pour réviser régulièrement permettra également d’améliorer son niveau et ses connaissances. Pour ce faire, les étudiants de Maths Sup peuvent s’entraîner sur différents chapitres, par exemple :

