Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices: Sommes et produits
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en Maths Sup
Exercices – sommes et produits MPSI, PCSI
1. QCM – Vrai/Faux
Les relations suivantes sont- elles vraies ? Les corriger lorsqu’elles sont fausses.
Question 1
Si ![]() ,
, 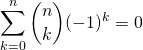 .
.
Question 2
Si ![]() ,
, 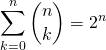 .
.
Question 3
Soit ![]() .
. 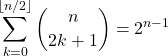 .
.
Question 4
Soit ![]() .
. 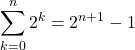 .
.
Question 5
Si ![]() et
et ![]() ,
, 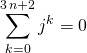 .
.
Question 6
Soient ![]() et
et ![]() une famille de complexes.
une famille de complexes.
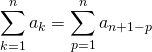 .
.
Question 7
Soient ![]() et
et ![]() une suite réelle ou complexe.
une suite réelle ou complexe.
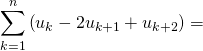
![]() .
.
Question 8
Soient ![]() et
et ![]() une suite réelle ou complexe.
une suite réelle ou complexe.
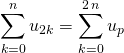 .
.
Question 9
Soit ![]() .
. 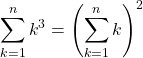 .
.
Question 10
Si ![]() ,
,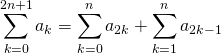
Question 11
Soient ![]() et
et ![]() ,
, ![]() deux familles réelles ou complexes
deux familles réelles ou complexes
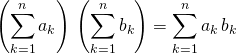 .
.
Question 12
Soit ![]() ,
, 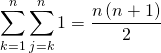
Question 13
Si 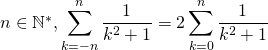
Question 14
Soit ![]() .
.
Si 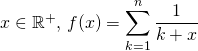 .
.
a) Si ![]() ,
, 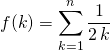 .
.
b) ![]() .
.
Question 15
Soient ![]() et
et ![]() une famille réelle ou complexe.
une famille réelle ou complexe.
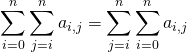 .
.
Question 16
Soient ![]() et
et ![]() et
et ![]() des complexes
des complexes
![]()
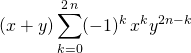 .
.
Question 17
Soient ![]() et
et ![]() des entiers tels que
des entiers tels que ![]() ,
, 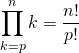
Question 18
Soient ![]() et
et ![]() des entiers tels que
des entiers tels que ![]() ,
, ![]() et
et![]() une famille de complexes.
une famille de complexes.
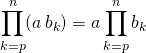 .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Des sommes et des coefficients du binôme
Exercice 1
Si ![]() , calculer
, calculer 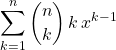
et 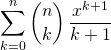 .
.
Exercice 2
Appliquer la formule du triangle de Pascal pour calculer 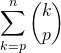 lorsque
lorsque ![]() .
.
Exercice 3
Démontrer par récurrence que si ![]() ,
, 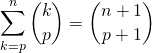 .
.
Exercice 4
Utiliser 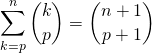 pour calculer
pour calculer![]() ,
, ![]() et
et ![]() .
.
3. Des calculs de sommes
Exercice 1
Si ![]() ,
, 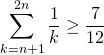 .
.
Exercice 2
Soit ![]() .
.
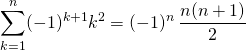
Exercice 3
Soit ![]() .
.
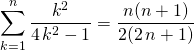
Exercice 4
Soit ![]() . Calculer
. Calculer 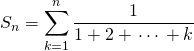 .
.
Exercice 5 Formule de Vandermonde
Soit ![]() .
. 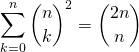 .
.
Exercice 6
Soit ![]() . Calculer
. Calculer 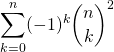
Exercice 7
Soit ![]() et
et ![]() une famille de réels telle que
une famille de réels telle que
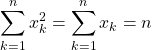 ,
,
alors ![]()
Exercice 8
Si 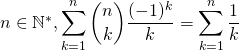
Exercice 9
Si ![]() , calculer
, calculer 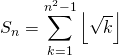
Exercice 10
Calculer si ![]() ,
,
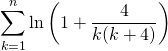 .
.
4. Calcul de produits
Exercice 1
Si ![]() et
et ![]() , calculer
, calculer
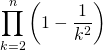 .
.
Exercice 2
Exprimer à l’aide factorielles
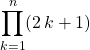 .
.
Exercice 3
Si ![]() et
et ![]()
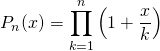 .
.
Question 1
Exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() lorsque
lorsque ![]() .
.
Question 2
Exprimer si ![]() ,
, ![]() à l’aide de coefficients du binôme.
à l’aide de coefficients du binôme.
Exercice 4
Si ![]() , simplifier
, simplifier 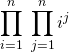 .
.
5. Sommes doubles
Exercice 1
Si ![]() , calculer
, calculer ![]() .
.
Exercice 2
Si ![]() , calculer
, calculer ![]() .
.
Exercice 3
Si ![]() , calculer
, calculer 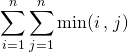 .
.
Exercice 4
Si ![]() , calculer
, calculer
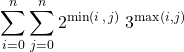 .
.
Exercice 5
Si ![]() et
et ![]() , calculer
, calculer
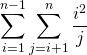 .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
6. Formule d’inversion de Pascal
Question 1
Soit ![]() .
.
Montrer que pour tout ![]() ,
, 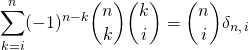
on note ![]() si
si ![]() et 1 si
et 1 si ![]() .
.
Question 2
Soit ![]() et
et ![]() et
et ![]() deux familles de réels ou complexes.
deux familles de réels ou complexes.
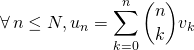
ssi 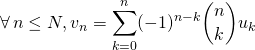 .
.
Pour aller plus loin dans les révisions, découvrez de nombreux autres chapitres de Maths au programme de MPSI, PCSI et PTSI dont :

