Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours sur l’intégration en Maths Sup MPSI, MP2I, PCSI, PTSI

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Maths Sup

Le simulateur d’admissibilité en prépa scientifique est un bon indicateur pour se rendre compte de l’importance des mathématiques dans les concours post-prépa. Les impasses en maths sont donc interdites dans le programme de Maths en MPSI, MP2I mais aussi en PCSI, ou PTSI. Progresser en maths à l’aide des cours de soutien en maths pour ne plus faire aucune impasse en maths sup.

A. Compléments sur la continuité et l’intégration en Maths Sup

1. Continuité uniforme en Maths Sup

$\bullet$ Une fonction $f$ définie sur l’intervalle $I$ à valeurs dans $\mathbb{K}$ est uniformément continue sur $I$ lorsque

$\forall\, \varepsilon \,\in \mathbb{R}^{+*}, \, \exists \, \alpha \in \mathbb{R}^{+*}, \, \forall \, (x , y) \in I^2$ ,

$\vert x - y \vert \leq \alpha \Rightarrow \vert f(x) - f(y) \vert \leq \varepsilon$ .

$\bullet$ Toute fonction uniformément continue sur l’intervalle $I$ est continue sur l’intervalle $I$ .

$\bullet$ Théorème de Heine.
Si $f$ est continue sur le segment $[a ,\, b]$ à valeurs dans $\mathbb{K}$ , elle est uniformément continue.

2. Fonction continue par morceaux sur un segment

Soit $f : [a,\, b] \to \mathbb{K}$ est dite continue par morceaux sur $[a , \, b]$ s’il existe une subdivision $(a_i)_{0 \leq i \leq n }$ de $[a , b]$ telle que pour tout $i \in [\![0 , n - 1]\!]$ , la restriction de $f$ à $]a _ i \, , \, a_{i + 1} [$ admet un prolongement par continuité $f_i$ défini sur $[a_i \, , \, a_{i + 1} ]$ .

Une telle subdivision est dite adaptée à $f$ .

Propriétés :

$\bullet$ L’ensemble des fonctions continues par morceaux sur $[a , b]$ à valeurs dans $\mathbb{K}$ est un $\mathbb{K}$ – espace vectoriel stable pour le produit des applications. On le note $\mathcal {C} _ m ([a , \, b] , \, \mathbb{K})$ .

$\bullet$ Si $f$ est continue par morceaux sur $[a , \, b]$ , $\vert f \vert$ est continue par morceaux sur $[a,\, b]$ .

$\bullet$ Toute fonction continue par morceaux sur $[a ,\, b]$ est bornée sur $[a , \, b]$ .

$\bullet$ Toute fonction en escalier (resp. continue) sur $[a , b]$ est continue par morceaux sur $[a, \, b]$ .

3. Intégrale d’une fonction continue par morceaux en Maths Sup

Soit $f$ continue par morceaux sur $[a , \, b]$ et $(a_i)_{0 \leq i \leq n }$ une subdivision adaptée à $f$ .

Pour tout $i \in [\![0 , n - 1]\!]$ , on note $f_i$ le prolongement par continuité à $[a_i \, , \, a_{i + 1} ]$ de la restriction de $f$ à $]a _ i \, , \, a_{i + 1} [$ .

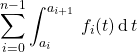Le réel $\displaystyle \sum _ {i = 0} ^{n - 1} \int_{a_i}^{a_{i + 1}} \, f_i (t) \, \textrm{d} \, t$ ne dépend pas de la subdivision adaptée choisie.

On l’appelle intégrale de $f$ sur $[a ,\, b]$ et on le note $\int_a ^b f(t) \, \textrm{d} \, t$ .

Propriétés :

$\bullet$ L’application $\mathcal {C} _ m ([a , b] , \, \mathbb{K}) \to \mathbb{K}$ , $f \mapsto \int_a ^b f(t) \, \textrm{d} \, t$ est linéaire.

$\bullet$ Si $(f , g) \in \mathcal {C} _ m ([a , b] , \, \mathbb{K})^2$ sont égales sauf en un nombre fini de points,

$\qquad \int_a ^b f(t) \, \textrm{d} \, t = \int_a ^b g(t) \, \textrm{d} \, t$ .

$\bullet$ Si $(f , g) \in \mathcal {C} _ m ([a , b] , \, \mathbb{K})^2$ vérifient sauf en un nombre fini de points $f(t) \leq g(t)$ ,

$\qquad \int_a ^b f(t) \, \textrm{d} \, t \leq \int_a ^b g(t) \, \textrm{d} \, t$ .

4. Intégrale d’une fonction continue en Maths Sup

Propriété :

Si $f$ est continue sur $[a, b]$ à valeurs dans $\mathbb{R}^+$

$\qquad \int_a ^b f(t) \, \textrm{d} \, t = 0$

$\quad \qquad$ ssi $\forall\, t \in [a , b],\, f(t) = 0$ .

Propriété :

Si $f$ est continue sur l’intervalle $I$ et si $a \in I$ , la fonction $x \mapsto \int_a ^x f(t) \, \textrm{d} \, t$ est la primitive $F$ de $f$ sur $I$ vérifiant $F(a) = 0$ .

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

B. Fonction $x \mapsto \int_{u(x)} ^{v(x)} f(t) \, \textrm{d} \, t$ en Maths Sup

On se place dans le cas où $F$ est définie par $F(x) = \displaystyle \int _{u(x)}^{v(x)} f(t) \, \textrm{d}\,t$ , $f$ étant continue.

1.Domaine de définition en Maths Sup

$\ast$ On cherche le domaine de définition $\Delta$ de $f$ . On suppose dans la suite que $f$ est continue sur $\Delta$ .

$\ast$ Puis on détermine l’ensemble des $x$ tels que $u(x)$ et $v(x)$ soient définis et tels que le segment d’extrémités $u(x)$ et $v(x)$ soit inclus dans un intervalle $I$ sur lequel $f$ est continue.

On note $\mathcal{D}$ le domaine de définition de $F$ .

2. Calcul de la dérivée en Maths Sup

Introduire une primitive $\Phi$ de $f$ sur un intervalle $I$ à préciser et écrire $\qquad \quad F(x) = \Phi (v(x)) - \Phi(u(x))$ ; dériver alors les fonctions composées ainsi obtenues.

3. Comment trouver la limite de $F$ , lorsque $u$ et $v$ ont même limite $L$ et où $\displaystyle \lim_{t \to L} \vert f(t) \vert = \infty$ ?

Hypothèses :

$\displaystyle \lim_{x\to a} u(x) = \lim_{x\to a} v(x) = L$ et $\displaystyle \lim_{t \to L} \vert f(t) \vert = +\infty$ , $L$ étant un réel.

$\bullet$ M1 : On cherche un équivalent simple noté $g(t)$ de $f(t)$ lorsque $t$ tend vers $L$ . On note $h(t) = f(t) - g(t)$ .

$\ast$ On démontre que $h$ est prolongeable par continuité en $L$ .

$\ast$ On détermine un intervalle $I$ conte- nant $L$ sur lequel $h$ est continue et on introduit une primitive $H$ de $h$ sur $I$ .

$\ast$ On vérifie que $(u(x) , v(x)) \in I^ 2$ lorsque $x$ tend vers $a$ et en écrivant $\displaystyle \int_{u(x)} ^{v(x)} h(t) \, \textrm{d} \,t = H(v(x) ) - H(u(x))$ ,

on obtient

$\displaystyle \lim_{x \to a} \int_{u(x)} ^{v(x)} h(t) \, \textrm{d} \,t = H(L) - H(L) = 0$

$\ast$ Il reste à trouver $\displaystyle \lim_{x \to a} \int_{u(x)} ^{v(x)} g(t) \, \textrm{d} \,t$ pour trouver la limite de $F$ en $a$ .

$\bullet$ M2 : On peut aussi chercher à encadrer $f(t)$ et en déduire un encadrement de $F(x)$ par deux fonctions ayant même limite.

4. Comment trouver la limite de $F$ en $a$ lorsque $u$ et $v$ tendent vers $\infty$ ?

Hypothèses :

$\displaystyle \lim_{x \to a} u(x) = \lim_{x \to a} v(x) = \varepsilon \; \infty$ où $\varepsilon = \pm 1$ .

$\bullet$ M1 : Lorsque la fonction $f$ est monotone, on encadre $f(t)$ entre $f(u(x))$ et $f(v(x))$ (il faut faire attention à la position relative des réels $u(x$ ) et $v(x)$ ), puis on intègre entre $u(x$ ) et $v(x)$ (toujours en faisant attention à la position relative de $u(x)$ et $v(x)$ ), de façon à obtenir un encadrement de $F(x)$ .

On saura trouver la limite de $F(x)$

$\ast$ lorsque les deux fonctions encadrant $F$ ont même limite,

$\ast$ ou lorsqu’on a minoré $F$ par une fonction admettant $+\infty$ pour limite en $a$ ,

$\ast$ ou lorsqu’on a majoré $F$ par une fonction admettant $- \infty$ pour limite en $a$ .

$\bullet$ M2 : Lorsqu’il existe $\alpha \in \mathbb{R}$ tel que $\Phi : x \mapsto \int_{\alpha} ^x f(t) \, \textrm{d} \, t$ admette une limite finie $L$ en $\varepsilon\, \infty$ , en écrivant $\qquad F(x) = \Phi(u(x)) - \Phi(v(x))$ ,

on obtient $\displaystyle \lim _ {x \to a} F(x) = L - L = 0$ .

C. Comment intégrer une inégalité en Maths Sup ?

$\bullet$ 1 : Vérifier que l’inégalité $f\leq g$ est valable sur tout l’intervalle d’intégration,

$\ast$ si $a \leq b$ : on peut alors écrire $\qquad \quad \int_a^b f(t) \; \textrm{d} \, t \leq \int_a^b g(t) \; \textrm{d} \, t$

$\ast$ si $a > b$ : il faut écrire $\qquad \quad \int_a^b f(t) \; \textrm{d} \, t \geq \int_a^b g(t) \; \textrm{d} \, t$ .

$\bullet$ 2 : Quand on intègre une inégalité stricte, elle devient large sauf si l’on peut appliquer le résultat suivant :

si $f$ et $g$ sont continues sur $[a , \, b]$ où $a < b$ ,

si $\forall\; t \in [a ,\, b] ,\, f(t)\geq g(t)$

et s’il existe $c$ de $[a ,\, b]$ tel que $f(c) \neq g(c)$ ,

$\qquad \int_a^b f(t) \; \textrm{d} \, t < \int_a^b g(t) \; \textrm{d} \, t$ .

Dans ce cas, il est indispensable de justifier soigneusement le résultat :

$g - f$ est continue, positive et différente de la fonction nulle, donc son intégrale est strictement positive.

Dans de nombreux cas, on doit intégrer une inégalité obtenue en écrivant qu’une fonction est continue en $c$ , ou en écrivant la limite d’une suite :

$\bullet$ 1er cas :
Si cette inégalité est valable sur tout l’intervalle d’intégration : il n’y a pas de difficulté (sauf celle de faire attention à la position respective de $a$ et $b$ , bornes de l’intervalle d’intégration).

$\bullet$ 2ème cas :
On peut choisir les bornes de l’intervalle d’intégration telles que l’inégalité soit valable sur tout l’intervalle.

$\bullet$ 3ème cas :
On doit utiliser la relation de Chasles, de façon à se placer sur un segment sur lequel on puisse appliquer l’inégalité.

D. Comment déterminer la limite d’une suite d’intégrales ?

Il y a deux résultats à savoir justifier.
En deuxième année, vous aurez d’autres méthodes pour trouver la limite d’une suite d’intégrales.

$\bullet$ Si $f$ est continue par morceaux sur $[0 ,\, 1]$ , la suite $(I_n)_n$

où $\quad \qquad I_n = \int_{0} ^1 t ^n \, f(t) \, \textrm{d} \, t$ converge vers 0.

$\bullet$ Lemme de Lebesque
Si $f$ est une fonction de classe $C^1$ sur $[a,\, b]$ , $\displaystyle \lim_{\lambda \to + \infty} \int_a ^b f(t) \cos(\lambda \, t) \, \textrm{d} \, t = 0$ .

De même, on démontre que :

$\displaystyle \lim_{\lambda \to + \infty} \int_a ^b f(t) \sin(\lambda \, t) \, \textrm{d} \, t = 0$ .

et $\displaystyle \lim_{\lambda \to + \infty} \int_a ^b f(t) \textrm{e} ^{\textrm{i}\, \lambda \, t} \textrm{d} \, t = 0$ .

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

E. Utilisation de la formule de Taylor avec reste intégral

Le seul problème est de la retenir correctement.

Dans le doute, vérifiez qu’elle est correcte pour $n = 0$

Si $f$ est de classe $C ^{n + 1}$ sur l’intervalle $I$ à valeurs dans $\mathbb{K}$ ,
$\displaystyle f(x) = \sum _ {k = 0} ^n \frac {f ^{(k)}(a)} {k! } (x - a) ^k$ $\qquad \qquad \displaystyle +\, \int_a^x \frac {(x - t)^{n}} {n!} \; f ^{(n + 1)} (t) \, \textrm{d} \, t$ .

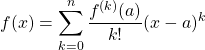
Elle peut être utilisée pour démontrer des inégalités comme dans le cas suivant.

On rappelle l’inégalité de Taylor-Lagrange :

Si $f$ est de classe $C ^{n + 1}$ sur l’intervalle $I$ à valeurs dans $\mathbb{K}$ , lorsque $f ^{(n +1)}$ est bornée sur $I$ , en notant

$\qquad M_{n + 1} = \displaystyle \sup _ {t \in I} \,\vert f ^{(n + 1)}(t) \vert$ ,

pour tout $(x , a) \in I^2$ ,

$\displaystyle \left \vert f(x) - \sum_ {k = 0} ^n \frac {f ^{(k)}(a)} {k! } (x - a) ^k \right \vert$ $\displaystyle \qquad \qquad \qquad \qquad \leq M_{n + 1} \frac {\vert x - a\vert ^{n + 1} } {(n + 1)! }$ .

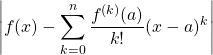
F. Sommes de Riemann

Si $f$ est continue par morceaux sur $[a , \, b]$ à valeurs dans $\mathbb{R}$ ou $\mathbb{C}$ ,

en notant

$R_n (f) = \displaystyle \frac {b - a} n \, \sum _{k = 0} ^{n - 1} f \left ( a +k \, \frac {b - a} n \right )$

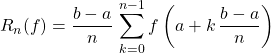
et 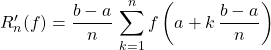$R'_n (f) = \displaystyle \frac {b - a} n \, \sum _{k = 1} ^n f \left ( a +k \, \frac {b - a} n \right )$

alors $\displaystyle \lim_{n \to + \infty} R_n(f) = \lim_{n \to + \infty} R'_n(f)$ $\qquad \qquad\qquad \qquad = \int_a^b f(t) \, \textrm{d} \, t$ .

On dit que $\int_a^b f(t) \, \textrm{d} \, t$ est limite des sommes de Riemann de $f$ associées aux subdivisions régulières de $[a \,, b]$ .

Les mathématiques sont une des matières les plus difficiles mais aussi une des matières les plus importantes en prépa scientifique. Cependant, parfois les élèves peuvent être confrontés à de grandes difficultés au cours de l’année, dans ce cas les cours particuliers en maths sont indispensables. De plus, entre deux cours particuliers, les étudiants peuvent continuer à réviser et s’entraîner de façon autonome grâce aux cours en ligne de Maths de MPSI, PCSI et PTSI :

Cours sur l’intégration en Maths Sup MPSI, MP2I, PCSI, PTSI

A. Compléments sur la continuité et l’intégration en Maths Sup

1. Continuité uniforme en Maths Sup

2. Fonction continue par morceaux sur un segment

3. Intégrale d’une fonction continue par morceaux en Maths Sup

4. Intégrale d’une fonction continue en Maths Sup

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

B. Fonction $x \mapsto \int_{u(x)} ^{v(x)} f(t) \, \textrm{d} \, t$ en Maths Sup

1.Domaine de définition en Maths Sup

2. Calcul de la dérivée en Maths Sup

3. Comment trouver la limite de $F$ , lorsque $u$ et $v$ ont même limite $L$ et où $\displaystyle \lim_{t \to L} \vert f(t) \vert = \infty$ ?

4. Comment trouver la limite de $F$ en $a$ lorsque $u$ et $v$ tendent vers $\infty$ ?

C. Comment intégrer une inégalité en Maths Sup ?

D. Comment déterminer la limite d’une suite d’intégrales ?

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

E. Utilisation de la formule de Taylor avec reste intégral

F. Sommes de Riemann

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Cours sur l’intégration en Maths Sup MPSI, MP2I, PCSI, PTSI

A. Compléments sur la continuité et l’intégration en Maths Sup

1. Continuité uniforme en Maths Sup

2. Fonction continue par morceaux sur un segment

3. Intégrale d’une fonction continue par morceaux en Maths Sup

4. Intégrale d’une fonction continue en Maths Sup

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

1.Domaine de définition en Maths Sup

2. Calcul de la dérivée en Maths Sup

C. Comment intégrer une inégalité en Maths Sup ?

D. Comment déterminer la limite d’une suite d’intégrales ?

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour réussir sa scolarité

En ligne ou à domicile

E. Utilisation de la formule de Taylor avec reste intégral

F. Sommes de Riemann

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Les meilleurs profs de maths pour
réussir sa scolarité