Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Polynômes en Maths Sup MPSI, PTSI, MP2I, PCSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Polynômes en Maths Sup
Plan :
1. Un problème de notation et de vocabulaire
2. Opérations sur les polynômes et degrés
3. Polynôme dérivé
4. Racines multiples
5. Comment démontrer qu’un polynôme divise un autre polynôme ?
6. Comment trouver le reste de la division de ![]() par
par ![]() ?
?
7. Nombre de racines d’un polynôme.
8. Comment factoriser un polynôme en produit de facteurs irréductibles ?
9. Polynômes scindés
10. Utiliser la notion d’espace vectoriel
On suppose dans tout ce chapitre sauf indication contraire que ![]() ou
ou ![]() .
.
1. Un problème de notation et de vocabulaire
1. Un polynôme ![]() peut être noté
peut être noté 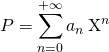 , en convenant que
, en convenant que ![]() si
si ![]() , mais lorsqu’il est de degré
, mais lorsqu’il est de degré ![]() , il peut aussi être noté
, il peut aussi être noté 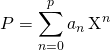 avec
avec ![]() .
.
L’égalité 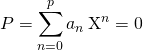 signifie que
signifie que ![]() .
.
![]() est l‘indéterminée du polynôme
est l‘indéterminée du polynôme ![]() , ce n’est ni un réel ni un complexe.
, ce n’est ni un réel ni un complexe.
On ne peut donc égaler ![]() à un réel ou un complexe (puisqu’un polynôme de degré
à un réel ou un complexe (puisqu’un polynôme de degré ![]() n’est pas égal à une constante qui est un polynôme de degré inférieur ou égal à 0).
n’est pas égal à une constante qui est un polynôme de degré inférieur ou égal à 0).
⚠️ Si l’on veut trouver les racines de ![]() dans le corps
dans le corps ![]() , il ne faut pas écrire
, il ne faut pas écrire ![]() , mais il faut prendre
, mais il faut prendre ![]() et résoudre l’équation algébrique
et résoudre l’équation algébrique ![]() .
.
2. Le polynôme 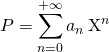 peut aussi être noté
peut aussi être noté ![]() .
.
La fonction polynôme associée au polynôme ![]() est la fonction notée
est la fonction notée ![]() , ou encore
, ou encore ![]() , définie par
, définie par 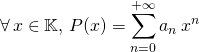 .
.
Il y a une bijection entre ![]() et l’ensemble des fonctions polynômes définies sur
et l’ensemble des fonctions polynômes définies sur ![]() ce qui permet si nécessaire d’identifier le polynôme
ce qui permet si nécessaire d’identifier le polynôme ![]() et sa fonction polynôme.
et sa fonction polynôme.
2. Opérations sur les polynômes et degrés
Dans ce paragraphe, ![]() peut aussi être égal à
peut aussi être égal à ![]() ou
ou ![]() .
.
Rappel
![]() et sinon
et sinon ![]() .
.
Si ![]() ,
, ![]() ssi
ssi ![]() est le plus grand entier
est le plus grand entier ![]() tel que
tel que ![]() .
.
On convient que ![]()
et si ![]()
![]() .
.
On note
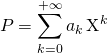 et
et 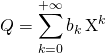 .
.
![]() M1. Somme
M1. Somme
![]()
![]() si
si ![]() ,
,
![]()
![]() si
si ![]() et
et ![]()
… si ![]() ,
, ![]()
… sinon, trouver le plus grand entier ![]() tel que
tel que ![]() .
.
![]() M2. Produit
M2. Produit
![]()
On rappelle que
![]() si
si 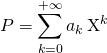 et
et 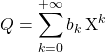 ,
,
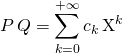
où ![]() .
.
![]() dans le cas où l’on écrit
dans le cas où l’on écrit
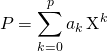 et
et 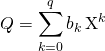
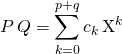 où si
où si ![]() ,
,
![]() .
.
![]() M3. Dérivées
M3. Dérivées
![]() Si
Si ![]() ,
, ![]()
![]() Si
Si ![]() et
et ![]() ,
, ![]() .
.
![]() M4. Si
M4. Si ![]() et
et ![]() ,
, ![]() .
.
![]() M5. Si
M5. Si ![]() et
et ![]() ,
,
![]() .
.
On rappelle que 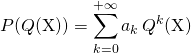 .
.
⚠️ Si ![]() , on fera attention à ne pas confondre
, on fera attention à ne pas confondre 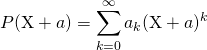 et le produit des polynômes
et le produit des polynômes ![]() et
et ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
3. Polynôme dérivé
3.1. Polynôme dérivé
![]() Définition Si
Définition Si 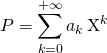 ,
, 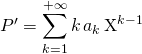
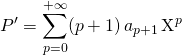
![]() Opérations Si
Opérations Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]() .
.
3.2. Dérivations successives
![]() Si
Si ![]() , on définit par récurrence :
, on définit par récurrence :
![]() et si
et si ![]()
![]() Si
Si 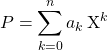 ,
, ![]() .
.
Si ![]() .
.
![]() Si
Si ![]() ,
, ![]() et
et ![]()
lorsque ![]()
![]()
et si ![]() .
.
![]() Formule de Leibniz
Formule de Leibniz
Si ![]() et
et ![]() ,
,
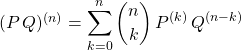 .
.
3.3. Formule de Taylor
Si ![]() est non nul et
est non nul et ![]() ,
,
si![]() ,
, 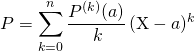 .
.
![]() M1. Si
M1. Si 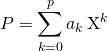 ,
, ![]() .
.
4. Racines multiples
![]() Si
Si ![]() ,
, ![]() et
et ![]() , il y a équivalence entre
, il y a équivalence entre
![]()
![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]()
![]()
![]() divise
divise ![]() et
et ![]() ne divise pas
ne divise pas ![]() .
.
![]() Il existe
Il existe ![]() tel que
tel que ![]() avec
avec ![]()
![]()
![]() et
et ![]() .
.
![]() Si
Si ![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]() ,
, ![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]() .
.
![]() Si
Si ![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]() ,
, ![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]()
![]() Si
Si ![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]() ,
, ![]() est racine d’ordre
est racine d’ordre ![]() de
de ![]() .
.
![]() Si
Si ![]() est racine de
est racine de ![]() ,
, ![]() admet un ordre de multiplicité inférieur ou égal au degré de
admet un ordre de multiplicité inférieur ou égal au degré de ![]() .
.
5. Comment démontrer qu’un polynôme divise un autre polynôme ?
🧡 Théorème de division euclidienne
Si ![]() avec
avec ![]() , il existe un unique couple
, il existe un unique couple ![]() tel que
tel que ![]()
![]() où
où ![]() .
.
![]() est le reste de la division euclidienne de
est le reste de la division euclidienne de ![]() par
par ![]() .
.
![]() est le quotient de la division euclidienne de
est le quotient de la division euclidienne de ![]() par
par ![]() .
.
Si ![]() ,
, ![]() divise
divise ![]() s’il existe
s’il existe ![]() tel que
tel que ![]() .
.
![]() M1. Le polynôme
M1. Le polynôme ![]() est divisible par
est divisible par ![]() ssi
ssi ![]() .
.
![]() M2. Si
M2. Si ![]() sont
sont ![]() éléments de
éléments de ![]() deux à deux distincts,
deux à deux distincts,
le polynôme ![]() est divisible par
est divisible par ![]() ssi
ssi ![]() .
.
![]() M3. Soient
M3. Soient ![]() et
et ![]() .
.
Le polynôme ![]() est divisible par
est divisible par ![]() ssi
ssi ![]() .
.
![]() M4. Si
M4. Si ![]() où
où ![]() , on note
, on note ![]() .
.
En conséquence de la formule de Taylor,
![]()
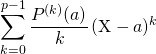 est le reste de la division de
est le reste de la division de ![]() par
par ![]()
![]()
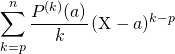 est le quotient de la division de
est le quotient de la division de ![]() par
par ![]() .
.
![]() M5. Si
M5. Si ![]() sont
sont ![]() éléments de
éléments de ![]() deux à deux distincts, tels que
deux à deux distincts, tels que ![]() ,
, ![]() divise
divise ![]() , le produit
, le produit 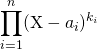
divise ![]() dans
dans ![]() .
.
![]() M6. Le polynôme
M6. Le polynôme ![]() est divisible par
est divisible par ![]() où
où ![]() ssi
ssi ![]() où
où ![]() est l’une des deux racines complexes de
est l’une des deux racines complexes de ![]() .
.
![]() M7. Soient
M7. Soient ![]() et
et ![]() .
.
Si ![]() divise
divise ![]() , le polynôme
, le polynôme ![]() divise
divise ![]() .
.
exemple :
CNS pour que ![]() divise
divise ![]() lorsque
lorsque ![]()
Correction : ![]() a pour racines
a pour racines ![]() et
et ![]() .
.
![]() divise
divise ![]() ssi
ssi ![]()
or ![]()
![]()
![]() .
.
6. Comment trouver le reste de la division de  par
par  ?
?
![]() M1. Le reste de la division de
M1. Le reste de la division de ![]() par
par ![]() est égal à
est égal à ![]() .
.
![]() M2. Si
M2. Si ![]() sont
sont ![]() éléments de
éléments de ![]() deux à deux distincts, on détermi- ne le reste de la division de
deux à deux distincts, on détermi- ne le reste de la division de ![]() par
par 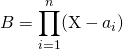 en écrivant que le reste
en écrivant que le reste ![]() est de degré strictement inférieur à
est de degré strictement inférieur à ![]() donc de la forme
donc de la forme 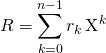 , que
, que ![]() et en introduisant les
et en introduisant les ![]() équations :
équations : ![]() ,
, ![]() on obtient un système linéaire de
on obtient un système linéaire de ![]() équations à
équations à ![]() inconnues permettant de déterminer les
inconnues permettant de déterminer les ![]() .
.
exemple 1 : Reste de la division de ![]() par
par ![]() .
.
exemple 2 : Reste de la division de ![]() par
par ![]() .
.
Correction :
Il existe ![]() tel que
tel que ![]() avec
avec ![]() , donc
, donc ![]() où
où ![]() et
et ![]() sont deux réels.
sont deux réels.
Comme ![]() et
et ![]() , on obtient
, on obtient ![]() et
et ![]() donc
donc ![]() et
et ![]() . Le reste est égal à
. Le reste est égal à ![]() .
.
exemple 2
![]() et
et ![]() .
.
Il existe ![]() tel que
tel que ![]() avec
avec ![]() , donc
, donc ![]() où
où ![]() et
et ![]() sont deux réels.
sont deux réels.
Comme ![]() .
.
![]() Si
Si ![]() ,
, ![]() avec
avec ![]() et
et ![]() réels, donc
réels, donc ![]() et
et ![]() , le reste est égal à
, le reste est égal à ![]() .
.
![]() Si
Si ![]() ,
, ![]() avec
avec ![]() et
et ![]() réels, donc
réels, donc ![]() et
et ![]() , le reste est
, le reste est ![]() .
.
On remarque que ![]() divise
divise ![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
![]() M3. Pour déterminer le reste
M3. Pour déterminer le reste ![]() de la division de
de la division de ![]() par
par ![]() , on écrit que
, on écrit que ![]() est divisible par
est divisible par ![]() , c’est-à-dire que
, c’est-à-dire que
![]() ,
,
Donc 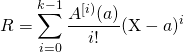 en utilisant la formule de Taylor.
en utilisant la formule de Taylor.
exemple 3
Reste de la division de ![]() où
où ![]() par
par ![]() .
.
Correction : Le reste ![]() de la division par
de la division par ![]() est un polynôme de degré inférieur ou égal à
est un polynôme de degré inférieur ou égal à ![]() qui vérifie :
qui vérifie : ![]() est divisible par
est divisible par ![]()
donc ![]() et
et ![]()
soit ![]() et
et ![]() .
.
Par la formule de Taylor, ![]()
![]()
![]() .
.
7. Nombre de racines d’un polynôme
7.1. Théorème de D’Alembert-Gauss.
Si ![]() est de degré au moins égal à 1,
est de degré au moins égal à 1, ![]() admet au moins une racine réelle.
admet au moins une racine réelle.
Le nombre de racines distinctes d’un polynôme de degré ![]() est majoré par
est majoré par ![]() .
.
7.2. Comment utiliser qu’un polynôme de degré ![]() admet au plus
admet au plus ![]() racines distinctes ?
racines distinctes ?
![]() M1. Pour démontrer que le polynôme
M1. Pour démontrer que le polynôme ![]() est nul, il suffit de prouver que
est nul, il suffit de prouver que ![]() a une infinité de zéros.
a une infinité de zéros.
M1bis. Pour prouver que ![]() est nul, on peut raisonner par l’absurde et supposer que
est nul, on peut raisonner par l’absurde et supposer que ![]() est de degré
est de degré ![]() . Si l’on peut trouver
. Si l’on peut trouver ![]() racines distinctes de
racines distinctes de ![]() ,
, ![]() est nul.
est nul.
M1ter. Pour démontrer que les polynômes ![]() et
et ![]() sont égaux, il suffit de trouver
sont égaux, il suffit de trouver ![]() racines distinctes de
racines distinctes de ![]() lorsque
lorsque ![]() .
.
![]() M2. Un polynôme à coefficients réels de degré impair a au moins une racine réelle.
M2. Un polynôme à coefficients réels de degré impair a au moins une racine réelle.
Le nombre de racines non réelles d’un polynôme à coefficients dans ![]() est pair.
est pair.
![]() M3. Les seuls polynômes périodi- ques sont les polynômes constants, ou ce qui est équivalent :
M3. Les seuls polynômes périodi- ques sont les polynômes constants, ou ce qui est équivalent :
si ![]() vérifie : il existe
vérifie : il existe ![]() tel que
tel que ![]() ,
,
![]() est constant.
est constant.
7.3. Application aux polynômes d’interpolation de Lagrange
(en exercice en PCSI).
Soient ![]()
![]() éléments de
éléments de ![]() , deux à deux distincts.
, deux à deux distincts.
Résultat 1
Pour tout ![]() de
de ![]() il existe un unique polynôme
il existe un unique polynôme ![]() tel que
tel que
![]() ,
, ![]() .
.
Les polynômes ![]() sont appelés polynômes d’interpolation de Lagrange sur les points
sont appelés polynômes d’interpolation de Lagrange sur les points ![]()
Résultat 2
Pour tout ![]() de
de ![]() ,
,
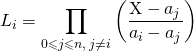 .
.
Résultat 3
![]() ,
, ![]() tel que
tel que ![]() ,
, ![]() , de plus
, de plus ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
8. Comment factoriser un polynôme en produit de facteurs irréductibles ?
Rappel :
![]() Les polynômes irréductibles de
Les polynômes irréductibles de ![]() sont les polynômes de degré 1.
sont les polynômes de degré 1.
![]() Les polynômes irréductibles de
Les polynômes irréductibles de ![]() sont les polynômes de degré 1 et les polynômes
sont les polynômes de degré 1 et les polynômes ![]() où
où ![]() ,
, ![]() et
et ![]() sont des réels tels que
sont des réels tels que ![]() et
et ![]() .
.
![]() Tout polynôme de
Tout polynôme de ![]() de degré au moins égal à 1 s’écrit d’une unique façon (à l’ordre près des facteurs) comme produit de polynômes irréduc- tibles dans
de degré au moins égal à 1 s’écrit d’une unique façon (à l’ordre près des facteurs) comme produit de polynômes irréduc- tibles dans ![]() .
.
C’est-à-dire
![]() Si
Si ![]() n’est pas constant de coefficient dominant
n’est pas constant de coefficient dominant ![]() , il existe
, il existe ![]() , des complexes
, des complexes ![]() deux à deux distincts et des entiers
deux à deux distincts et des entiers ![]() strictement positifs tels que
strictement positifs tels que
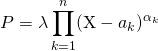 .
.
![]() Si
Si ![]() n’est pas constant de coefficient dominant
n’est pas constant de coefficient dominant ![]() , il existe
, il existe
… ![]() , des complexes
, des complexes ![]() deux à deux distincts et des entiers
deux à deux distincts et des entiers ![]() strictement positifs,
strictement positifs,
… ![]() et une famille de couples deux à deux distincts
et une famille de couples deux à deux distincts ![]() tels que
tels que ![]() et une famille d’entiers strictement positifs
et une famille d’entiers strictement positifs ![]()
tels que ![]() s’écrive :
s’écrive :
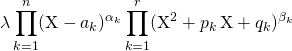 .
.
Il y a unicité à l’ordre près des facteurs de cette décomposition.
⚠️ dans la factorisation, ne pas oublier de multiplier par le coefficient domi- nant.
![]() M1. Pour factoriser un polynôme bicarré, on l’écrit sous la forme
M1. Pour factoriser un polynôme bicarré, on l’écrit sous la forme ![]() .
.
exemple 1 : Factoriser dans ![]()
![]() et
et ![]() .
.
![]() M2. Pour factoriser un polynôme
M2. Pour factoriser un polynôme ![]() dans
dans ![]() (lorsque la décomposition n’est pas évidente), on cherche les racines de
(lorsque la décomposition n’est pas évidente), on cherche les racines de ![]() .
.
On les classe en
![]() racines réelles
racines réelles
![]() racines complexes non réelles que l’on regroupe deux par deux en racines conjuguées .
racines complexes non réelles que l’on regroupe deux par deux en racines conjuguées .
Ne pas oublier devant la factorisation le coefficient dominant du polynôme .
![]() M3. Pour factoriser dans
M3. Pour factoriser dans ![]() un polynôme de la forme
un polynôme de la forme ![]() ou
ou ![]() (ou tout polynôme faisant intervenir les racines
(ou tout polynôme faisant intervenir les racines ![]() -ièmes d’un complexe) :
-ièmes d’un complexe) :
ces racines ![]() -ièmes dépendent d’un entier
-ièmes dépendent d’un entier ![]() qui doit prendre
qui doit prendre ![]() valeurs consécutives entières.
valeurs consécutives entières.
👍 Choisir si possible ces valeurs consécutives de façon à pouvoir regrouper facilement les racines conjuguées.
exemple 3 : Factoriser ![]() et
et ![]() dans
dans ![]() .
.
9. Polynômes scindés
D : Un polynôme ![]() de degré
de degré ![]() est scindé sur
est scindé sur ![]() lorsqu’on peut l’écrire sous l’une des deux formes suivantes :
lorsqu’on peut l’écrire sous l’une des deux formes suivantes :
![]()
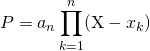
où ![]() est une famille de
est une famille de ![]() éléments de
éléments de ![]() et
et ![]() son coefficient dominant.
son coefficient dominant.
![]() Il existe
Il existe ![]() une famille
une famille ![]() d’éléments 2 à 2 distincts de
d’éléments 2 à 2 distincts de ![]() et une famille
et une famille ![]() , de somme égale à
, de somme égale à ![]() tels que
tels que 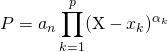
où ![]() est son coefficient dominant.
est son coefficient dominant.
![]() Si
Si ![]() de degré
de degré ![]() est scindé sur
est scindé sur ![]() et si
et si ![]() sont ses
sont ses ![]() racines, lorsque
racines, lorsque 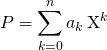 ,
,
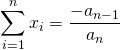
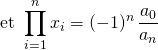 .
.
🧡 Savoir démontrer les résultats suivants
![]() R1 : Si
R1 : Si ![]() est scindé sur
est scindé sur ![]() à racines distinctes de degré
à racines distinctes de degré ![]() ,
, ![]() est scindé sur
est scindé sur ![]() à racines distinctes.
à racines distinctes.
![]() R2 : Si
R2 : Si ![]() est scindé sur
est scindé sur ![]() de degré
de degré ![]() ,
, ![]() est scindé sur
est scindé sur ![]() .
.
![]() R3. Si
R3. Si 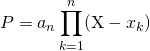
lorsque ![]() ,
,
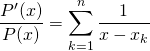 .
.
![]() R4. Si
R4. Si 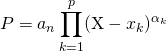
lorsque ![]() ,
,
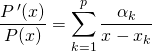 .
.
10. Utiliser la notion d’espace vectoriel
Une compilation de résultats sur les polynômes et espaces vectoriels
![]()
![]() est un
est un ![]() -espace vectoriel de dimension infinie, stable par multipli- cation.
-espace vectoriel de dimension infinie, stable par multipli- cation.
![]() Si
Si ![]() est une famille de polynômes de degrés 2 à 2 distincts, c’est une famille libre de
est une famille de polynômes de degrés 2 à 2 distincts, c’est une famille libre de ![]() .
.
![]() Si
Si ![]() ,
, ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() , de dimension
, de dimension ![]() .
.
![]()
![]() est la base canon- ique de
est la base canon- ique de ![]() .
.
![]() Si
Si ![]()
![]() est de degré
est de degré ![]() ,
, ![]() est une base de
est une base de ![]() .
.
![]() Si
Si ![]() est de degré
est de degré ![]() ,
, ![]()
est une base de ![]() .
.
![]() Soient
Soient ![]() ,
, ![]() éléments de
éléments de ![]() , deux à deux distincts. La famille
, deux à deux distincts. La famille ![]() des polynômes d’interpolation de Lagrange sur les points
des polynômes d’interpolation de Lagrange sur les points ![]() est une base de
est une base de ![]() . Pour tout
. Pour tout ![]() ,
, 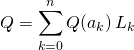 . (MPSI seulement)
. (MPSI seulement)
Si vous maîtrisez le chapitre sur les polynômes, prenez de l’avance en combinant avec les cours de maths sur les révisions des chapitres qui vont suivre comme :

