Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours sur l’espace préhilbertiens de Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Le chapitre sur l’espace préhilbertien est un des chapitres les plus importants dans le programme de MPSI en Maths. Profitez de ce cours en ligne et nos cours de maths particulier pour revoir les notions de cours fondamentales ainsi que les méthodes et propriétés à connaître par cœur. Vous pourrez ainsi augmenter vos résultats et votre moyenne.
A. Démontrer que l’on a défini un produit scalaire en Maths Sup
![]() M1 : Si
M1 : Si ![]() est un
est un ![]() -espace vectoriel,
-espace vectoriel,
![]() vérifier que
vérifier que ![]()
est une forme bilinéaire symétrique en démontrant les deux propriétés :
… ![]() est linéaire
est linéaire
… et ![]() .
.
![]() puis montrer que
puis montrer que ![]() est positive non dégénérée en prouvant que :
est positive non dégénérée en prouvant que :
… ![]()
… ![]()
ce qui est plus simple en général que de prouver que : ![]() .
.
![]() M2 : Connaître les produits scalaires au programme.
M2 : Connaître les produits scalaires au programme.
![]() Sur
Sur ![]() , le produit scalaire canonique défini pour
, le produit scalaire canonique défini pour ![]()
et ![]()
par
![]() .
.
![]() Sur
Sur ![]() , le produit scalaire canonique :
, le produit scalaire canonique :
si ![]() et
et ![]()
![]() .
.
![]() Sur l’espace vectoriel
Sur l’espace vectoriel ![]() des fonctions continues sur
des fonctions continues sur ![]() à valeurs dans
à valeurs dans ![]() ,
,
![]() .
.
![]() le résultat classique à savoir démontrer : Soit
le résultat classique à savoir démontrer : Soit ![]() .
.
![]() définit un produit scalaire sur
définit un produit scalaire sur ![]() .
.
![]() Si
Si ![]() est un produit scalaire sur l’espace vectoriel réel
est un produit scalaire sur l’espace vectoriel réel ![]() , on dit que
, on dit que ![]() est un espace préhilbertien réel.
est un espace préhilbertien réel.
Si de plus ![]() est de dimension finie, on dit que
est de dimension finie, on dit que ![]() est un espace euclidien.
est un espace euclidien.
![]() Savoir utiliser la bilinéarité du produit scalaire :
Savoir utiliser la bilinéarité du produit scalaire :
On suppose que ![]() est un préhilbertien,
est un préhilbertien,
![]() Si
Si ![]() et
et ![]() ,
,
![]()
![]()
![]() Plus généralement, si
Plus généralement, si ![]() vérifient
vérifient ![]() ,
,
![]()
et ![]()
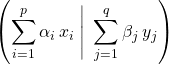
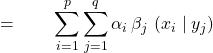 .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
B. Définir et manipuler une norme euclidienne en Maths Sup
Si ![]() est un produit scalaire sur
est un produit scalaire sur ![]() , on définit la norme euclidienne de
, on définit la norme euclidienne de ![]()
par ![]() .
.
Alors ![]() vérifie
vérifie
![]()
![]() ssi
ssi ![]()
![]() Si
Si ![]() et
et ![]() ,
,![]()
![]() Si
Si ![]() ,
, ![]() (inégalité triangulaire).
(inégalité triangulaire).
On dit que ![]() est une norme euclidienne sur
est une norme euclidienne sur ![]() .
.
On dit que ![]() est unitaire lorsque
est unitaire lorsque ![]() .
.
Cas particuliers :
![]() La norme euclidienne sur
La norme euclidienne sur ![]() est définie si
est définie si ![]() par :
par :
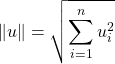 .
.
![]() La norme euclidienne de
La norme euclidienne de ![]() ,
, ![]() .
.
Connaître la formule de polarisation
Si ![]()
![]() .
.
On peut aussi démontrer que
![]() .
.
P : On note ![]() un préhilbertien réel.
un préhilbertien réel.
Soient ![]() ,
, ![]() ,
, ![]() et
et ![]() ,
,
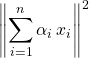
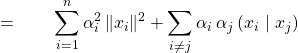 .
.
C. Manipuler l’inégalité de Cauchy-Schwarz en Maths Sup
![]() Le résultat général
Le résultat général
Si ![]() est un préhilbertien réel, on peut utiliser l’inégalité de Cauchy-Schwarz :
est un préhilbertien réel, on peut utiliser l’inégalité de Cauchy-Schwarz :
![]()
Il y a égalité si, et seulement si, la famille ![]() est liée.
est liée.
![]() L’écriture dans
L’écriture dans ![]()
Si ![]() et
et ![]() sont deux familles de
sont deux familles de ![]() réels,
réels,
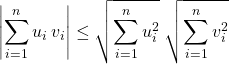
ce qui est équivalent à
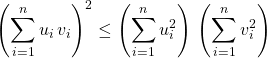
![]() L’écriture dans
L’écriture dans ![]()
si ![]() et
et ![]() sont éléments de
sont éléments de ![]() ,
,
![]()
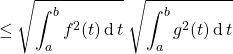
ou encore
![]()
![]()
D. Manipuler la notion d’orthogonalité en Maths Sup
![]() M1 : Deux vecteurs
M1 : Deux vecteurs ![]() et
et ![]() de
de ![]() sont orthogonaux ssi
sont orthogonaux ssi ![]() ssi
ssi ![]() (théorème de Pythagore).
(théorème de Pythagore).
On écrit ![]() .
.
![]() M2 : Si
M2 : Si ![]() est une partie non vide de
est une partie non vide de ![]() , l’ensemble des vecteurs orthogonaux à tous les vecteurs de
, l’ensemble des vecteurs orthogonaux à tous les vecteurs de ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() qui est noté
qui est noté ![]() et appelé orthogonal de
et appelé orthogonal de ![]() .
.
![]() .
.
![]() M3 : Pour démontrer qu’un vecteur
M3 : Pour démontrer qu’un vecteur ![]() de
de ![]() préhilbertien réel est nul, on peut
préhilbertien réel est nul, on peut
![]() démontrer que
démontrer que ![]()
![]() démontrer que
démontrer que ![]() , c’est-à-dire que
, c’est-à-dire que ![]() .
.
![]() M4 : Si
M4 : Si ![]() est un sous-espace vectoriel du préhilbertien réel
est un sous-espace vectoriel du préhilbertien réel ![]() ,
,
![]() .
.
![]() M5 : Toute famille finie de vecteurs 2 à 2 orthogonaux et non nuls est libre.
M5 : Toute famille finie de vecteurs 2 à 2 orthogonaux et non nuls est libre.
E. Construire une famille orthonormale en Maths Sup
Dans ce paragraphe, ![]() est un préhilbertien réel.
est un préhilbertien réel.
![]() M1 : Connaître le résultat complet du principe d’orthonormalisation de Gram-Schmidt
M1 : Connaître le résultat complet du principe d’orthonormalisation de Gram-Schmidt
Si ![]() est une famille libre du préhilbertien de
est une famille libre du préhilbertien de ![]() , il existe une unique famille orthonormale
, il existe une unique famille orthonormale ![]() de
de ![]() telle que
telle que
pour tout ![]() ,
,
![]() .
.
et ![]() .
.
![]() M2 : Application pratique du procédé d’orthonormalisation de Gram-Schmidt :
M2 : Application pratique du procédé d’orthonormalisation de Gram-Schmidt :
![]() Introduire une famille libre
Introduire une famille libre ![]() de
de ![]() .
.
![]() Poser
Poser ![]() .
.
Puis construire les vecteurs par récurrence
![]() après avoir construit
après avoir construit ![]() , introduire si
, introduire si ![]()
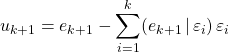
puis calculer ![]() .
.
Théorème :
Dans le cas où ![]() est de dimension finie et où
est de dimension finie et où ![]() est une base de
est une base de ![]() , on construit ainsi une base orthonormale
, on construit ainsi une base orthonormale ![]() de
de ![]() .
.
Tout sous-espace vectoriel de dimension finie strictement positive de ![]() admet une base orthonormale.
admet une base orthonormale.
F. Utiliser l’orthogonal d’un sev de dimension finie en Maths Sup
Dans ce paragraphe, ![]() est un sous-espace vectoriel (sev) de dimension finie du préhilbertien
est un sous-espace vectoriel (sev) de dimension finie du préhilbertien ![]() .
.
![]() Si
Si ![]() ,
, ![]() admet une base orthonormale.
admet une base orthonormale.
![]()
![]() .
.
![]() La projection de
La projection de ![]() sur
sur ![]() parallèle- ment à
parallèle- ment à ![]() est appelée projection orthogonale sur
est appelée projection orthogonale sur ![]() et notée
et notée ![]() .
.
![]() Si
Si ![]() et si
et si ![]() est une base orthonormale de
est une base orthonormale de ![]() , la projection orthogonale sur
, la projection orthogonale sur ![]() est définie par
est définie par
![]() .
.
![]() Si
Si ![]() est la projection orthogonale sur
est la projection orthogonale sur ![]() , pour tout
, pour tout ![]() ,
,
![]() .
.
On en déduit que ![]() .
.
![]() Si
Si ![]() ,
, ![]() admet un plus petit élément appelé distance de
admet un plus petit élément appelé distance de ![]() à
à ![]() et noté
et noté ![]() .
.
Ce mininum est atteint en un seul point ![]() .
.
Donc ![]()
et ![]() .
.
G. Reconnaître et résoudre un problème de distance à un sev
Dans ce paragraphe, ![]() est un espace préhilbertien réel.
est un espace préhilbertien réel.
Soit ![]() donné. Dans le cas où l’on demande de déterminer la borne inférieure de l’ensemble
donné. Dans le cas où l’on demande de déterminer la borne inférieure de l’ensemble ![]()
![]() étant à valeurs positives ou nulles, il y a de fortes chances de se trouver devant un problème de distance à un sous-espace vectoriel.
étant à valeurs positives ou nulles, il y a de fortes chances de se trouver devant un problème de distance à un sous-espace vectoriel.
Pour cela, il faut :
![]() 1. préciser l’espace vectoriel
1. préciser l’espace vectoriel ![]() considéré, lorsqu’il n’est pas donné par l’énoncé.
considéré, lorsqu’il n’est pas donné par l’énoncé.
![]() 2. trouver le produit scalaire utilisé.
2. trouver le produit scalaire utilisé.
![]() 3. trouver le sous-espace vectoriel
3. trouver le sous-espace vectoriel ![]() de dimension
de dimension ![]() , c’est-à-dire écrire
, c’est-à-dire écrire
![]() et interpréter le problème sous l’une des deux formes :
et interpréter le problème sous l’une des deux formes :
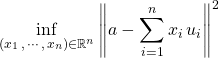
![]()
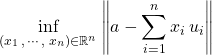
![]() .
.
![]() 4. définir le projeté orthogonal
4. définir le projeté orthogonal ![]() de
de ![]() sur
sur ![]() (cf § 6).
(cf § 6).
![]() 5. calculer
5. calculer
![]()
![]() ou
ou ![]()
(théorème de Pythagore).
N’hésitez pas à compléter vos révisions de cours en MPSI, PCSI et PTSI avec l’ensemble de nos autres cours en ligne de Maths pour les Maths Sup. Revoyez par exemple, les notions essentielles des chapitres qui suivent :

