Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Probabilités, cours de Maths en MPSI, MP2I, PCSI et PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Pour avoir de bonnes notes et une bonne moyenne en Maths Sup, il est essentiel de maîtriser l’ensemble des cours de maths au programme de Maths Sup. Pour ce faire, les étudiants en difficultés ou même les majors de prépa peuvent faire le choix de suivre des cours de maths pour maximiser leurs résultats.
A. Manipuler la notion d’événements en Maths Sup
![]() En SUP, on suppose que l’on effectue une expérience ayant un nombre fini de résultats et on note
En SUP, on suppose que l’on effectue une expérience ayant un nombre fini de résultats et on note ![]() l’ensemble de ces événements élémentaires. On dit que
l’ensemble de ces événements élémentaires. On dit que ![]() est l’univers des possibles.
est l’univers des possibles.
![]() Toute partie
Toute partie ![]() de
de ![]() est appelé événement. On dit que l’événement
est appelé événement. On dit que l’événement ![]() est réalisé lorsque le résultat de l’expérience appartient à
est réalisé lorsque le résultat de l’expérience appartient à ![]() .
.
![]() est toujours réalisé, on l’appelle événement certain.
est toujours réalisé, on l’appelle événement certain.
![]() n’est jamais réalisé, on l’appelle événement impossible.
n’est jamais réalisé, on l’appelle événement impossible.
![]() Si
Si ![]() et
et ![]() sont deux événements, on peut définir
sont deux événements, on peut définir
![]()
![]() , l’événement
, l’événement ![]() est réalisé lorsque
est réalisé lorsque ![]() n’est pas réalisé.
n’est pas réalisé.
![]()
![]() l’événement réalisé lorsque
l’événement réalisé lorsque ![]() et
et ![]() le sont.
le sont.
Les événements ![]() et
et ![]() sont incompatibles lorsque
sont incompatibles lorsque ![]() .
.
![]()
![]() l’événement réalisé lorsque l’un au moins des événements
l’événement réalisé lorsque l’un au moins des événements ![]() ,
, ![]() est réalisé.
est réalisé.
![]() L’événement
L’événement ![]() implique l’événement
implique l’événement ![]() lorsque
lorsque ![]() .
.
![]() Si
Si ![]() ,
, ![]() , la famille
, la famille ![]() est un système complet d’événements de
est un système complet d’événements de ![]() lorsque
lorsque
… ![]() ,
, ![]() est une partie non vide de
est une partie non vide de ![]()
… ![]()
… 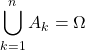 .
.
Pour modéliser une expérience, il faut définir l’univers des possibles ![]() et lui associer une probabilité comme dans le paragraphe suivant
et lui associer une probabilité comme dans le paragraphe suivant
.
B. Manipuler la notion de probabilité en MPSI, PCSI et PTSI
1. Utiliser la définition et les propriétés
![]() M1 : Connaître la définition :
M1 : Connaître la définition :
On suppose que ![]() est un ensemble fini.
est un ensemble fini.
On appelle probabilité sur l’univers ![]() toute application de
toute application de ![]() dans
dans ![]() telle que
telle que
![]()
![]()
![]() Si
Si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() disjointes,
disjointes, ![]() .
.
On dit que ![]() est un espace probabilisé fini..
est un espace probabilisé fini..
![]() M2 : Et les conséquences :
M2 : Et les conséquences :
Soit ![]() un espace probabilisé fini.
un espace probabilisé fini.
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
![]() si
si ![]() et
et ![]() vérifient
vérifient ![]() ,
, ![]() .
.
![]() Si
Si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() ,
,
![]()
![]() Soient
Soient ![]() ,
, ![]() et une famille
et une famille ![]() telle que si
telle que si ![]() ,
,
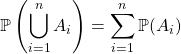 .
.
![]() Soient
Soient ![]() ,
, ![]() et une famille
et une famille ![]() ,
,
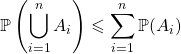 .
.
2. Caractériser une probabilité sur un univers fini
![]() Si
Si ![]() est un espace probabilisé fini, l’application
est un espace probabilisé fini, l’application
![]() ,
, ![]()
vérifie ![]() .
.
![]() Réciproquement, si
Réciproquement, si ![]() vérifie
vérifie
![]() , il existe une et une seule probabilité
, il existe une et une seule probabilité ![]() telle que
telle que ![]() .
.
Alors ![]() .
.
3. Équiprobabilité en Maths Sup
![]() Soit
Soit ![]() un univers fini de cardinal
un univers fini de cardinal ![]() . On dit que l’on est sous l’hypothèse d’équi-probabilité lorsque
. On dit que l’on est sous l’hypothèse d’équi-probabilité lorsque
![]() .
.
Alors ![]() .
.
![]() On est sous l’hypothèse d’équiprobabilité lorsque l’on tire au hasard en particulier dans les cas suivants :
On est sous l’hypothèse d’équiprobabilité lorsque l’on tire au hasard en particulier dans les cas suivants :
Si l’on a une urne ![]() de
de ![]() boules distinctes,
boules distinctes,
![]() tirages successifs avec remise de
tirages successifs avec remise de ![]() boules dans
boules dans ![]() :
:
![]() est l’ensemble des applications de
est l’ensemble des applications de ![]() dans
dans ![]() et
et ![]() .
.
![]() tirage de
tirage de ![]() boules en une seule fois dans
boules en une seule fois dans ![]() :
:
![]() est l’ensemble des parties de
est l’ensemble des parties de ![]() éléments parmi les
éléments parmi les ![]() boules.
boules.
![]() .
.
![]() tirages successifs de
tirages successifs de ![]() boules sans remise dans
boules sans remise dans ![]() :
:
![]() est l’ensemble des
est l’ensemble des ![]() -listes sans répétition des
-listes sans répétition des ![]() éléments de
éléments de ![]() .
.
![]() .
.
![]() Vider l’urne par tirages successifs :
Vider l’urne par tirages successifs :
![]() est l’ensemble des bijections de
est l’ensemble des bijections de ![]() sur
sur ![]() et
et ![]() .
.
4. Calculer la probabilité d’une réunion en Maths Sup
a. Cas d’événements deux à deux incompatibles
avant d’écrire 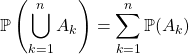 ,
,
vérifier que les événements ![]() sont deux à deux incompatibles.
sont deux à deux incompatibles.
b. Cas d’événements non deux à deux incompatibles
![]() Pour 2 événements :
Pour 2 événements :
![]()
![]() Savoir démontrer pour 3 événements
Savoir démontrer pour 3 événements
![]()
![]()
![]() .
.
5. Calcul de la probabilité d’un événement contenant l’expression « au moins «
Dans la suite on suppose que ![]() est l’événement » avoir au moins un élément vérifiant la propriété
est l’événement » avoir au moins un élément vérifiant la propriété ![]() « .
« .
a. Calcul de  }
}
![]() M1 Cas le plus simple : » avoir au moins une fois un élément vérifiant une propriété
M1 Cas le plus simple : » avoir au moins une fois un élément vérifiant une propriété ![]() « .
« .
On cherche la probabilité de ![]() :
:
» aucun élément ne vérifie la propriété ![]() « .
« .
![]() M2 (en général c’est plus compliqué) Si
M2 (en général c’est plus compliqué) Si ![]() est le nombre maximum d’éléments vérifiant la propriété
est le nombre maximum d’éléments vérifiant la propriété ![]() , on peut introduire
, on peut introduire ![]() : « avoir exactement
: « avoir exactement ![]() éléments vérifiant la propriété
éléments vérifiant la propriété ![]() » et écrire que
» et écrire que 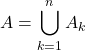 , les événements
, les événements ![]() étant deux à deux incompatibles,
étant deux à deux incompatibles, 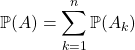 .
.
b. Calcul de 
![]()
par incompatiblité,
![]()
et ![]() .
.
Vous devriez savoir calculer ![]() et
et ![]() .
.
C. Probabilité conditionnelle en Maths Sup
1. Définition et propriété de probabilités en Maths Sup
Soit ![]() un espace probabilisé fini et
un espace probabilisé fini et ![]() tel que
tel que ![]() .
.
L’application ![]()
définit une probabilité sur ![]() appelée probabilité conditionnelle relative à
appelée probabilité conditionnelle relative à ![]() .
.
On note ![]() .
.
2. Formule des probabilités composées en Maths Sup
![]() est un espace probabilisé fini.
est un espace probabilisé fini.
![]() Si
Si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() telles que
telles que ![]() ,
, ![]() .
.
![]() Si
Si ![]() et si
et si ![]() sont des parties de
sont des parties de
![]() telles que
telles que 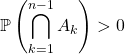 ,
,
toutes les probabilités conditionnelles suivantes sont définies et
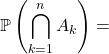
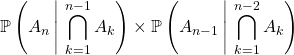
![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
3. Probabilités totales en Maths Sup
![]() Formule des probabilités totales
Formule des probabilités totales
Soit ![]() un espace probabilisé fini.
un espace probabilisé fini.
![]() Si
Si ![]() est un système complet d’événements de probabilité, pour tout
est un système complet d’événements de probabilité, pour tout ![]() ,
, 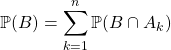 .
.
Si de plus ![]() ,
, 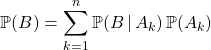 .
.
4. Formule de Bayes en Maths Sup
![]() Forme 1
Forme 1
Soient ![]() et
et ![]() deux événements de
deux événements de ![]() de probabilité non nulle :
de probabilité non nulle :
![]() .
.
![]() Forme 2
Forme 2
Soient ![]() un espace probabilisé fini et
un espace probabilisé fini et ![]() .
.
On suppose que ![]() et
et ![]() est un système complet d’événements de probabilité non nulle.
est un système complet d’événements de probabilité non nulle.
Si ![]() , pour tout
, pour tout ![]() ,
,
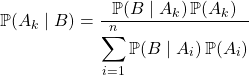
En cas particulier
Si ![]() sont deux événements tels que
sont deux événements tels que ![]() et
et ![]() ,
,
![]()
![]() .
.
5. Il faut distinguer les quantités  et
et 
a) Quand on calcule ![]() , on calcule la probabilité que
, on calcule la probabilité que ![]() et
et ![]() soient réalisés en même temps.
soient réalisés en même temps.
b) Quand on calcule ![]() , on calcule un quotient de probabilités :
, on calcule un quotient de probabilités :
![]() n’est pas un événement.
n’est pas un événement.
On sait que ![]() est réalisé et on cherche la probabilité que
est réalisé et on cherche la probabilité que ![]() soit réalisé lorsque
soit réalisé lorsque ![]() l’est.
l’est.
![]() Dans certains cas, il est évident que l’on demande une probabilité conditionnelle, car on demande la probabilité d’un événement sachant (ou lorsque) l’on a obtenu
Dans certains cas, il est évident que l’on demande une probabilité conditionnelle, car on demande la probabilité d’un événement sachant (ou lorsque) l’on a obtenu ![]() . On peut repérer cette situation en cherchant les mots « sachant », « si », « lorsque » dans l’énoncé.
. On peut repérer cette situation en cherchant les mots « sachant », « si », « lorsque » dans l’énoncé.
![]() Dans d’autres cas, on donne la réalisation de l’événement
Dans d’autres cas, on donne la réalisation de l’événement ![]() , dans une phrase du type « on a obtenu ? » et on demande ensuite de calculer la probabilité de
, dans une phrase du type « on a obtenu ? » et on demande ensuite de calculer la probabilité de ![]() , donc de calculer
, donc de calculer ![]() .
.
D. Quand appliquer la formule des probabilités totales en Maths Sup
![]() M1 Lorsque l’on fait des tirages qui peuvent avoir lieu dans des urnes différentes ou dans des conditions différentes qui sont définies par les résultats d’une première épreuve, il faut introduire un système complet d’événements correspondant aux différents choix des urnes ou des différents résultats de la première épreuve.
M1 Lorsque l’on fait des tirages qui peuvent avoir lieu dans des urnes différentes ou dans des conditions différentes qui sont définies par les résultats d’une première épreuve, il faut introduire un système complet d’événements correspondant aux différents choix des urnes ou des différents résultats de la première épreuve.
![]() M2 Lorsque les résultats de l’épreuve
M2 Lorsque les résultats de l’épreuve ![]() dépendent des résultats de l’épreuve
dépendent des résultats de l’épreuve ![]() , introduire un système complet d’événements correspondant à toutes les éventualités du rang
, introduire un système complet d’événements correspondant à toutes les éventualités du rang ![]() et utiliser la formule des probabilités totales.
et utiliser la formule des probabilités totales.
![]() M3 Lorsque les résultats de l’épreuve
M3 Lorsque les résultats de l’épreuve ![]() dépendent des résultats de toutes les épreuves précédentes, introduire un système complet d’événements correspondant à toutes les éventualités des premières épreuves permettant soit de terminer l’ensemble des épreuves soit de « remettre le compteur à zéro » et utiliser la formule des probabilités totales.
dépendent des résultats de toutes les épreuves précédentes, introduire un système complet d’événements correspondant à toutes les éventualités des premières épreuves permettant soit de terminer l’ensemble des épreuves soit de « remettre le compteur à zéro » et utiliser la formule des probabilités totales.
Si ![]() est un des événements du système complet précédent correspondant à
est un des événements du système complet précédent correspondant à ![]() épreuves, on sera donc amené à calculer des probabilités du type
épreuves, on sera donc amené à calculer des probabilités du type ![]() : il reste
: il reste ![]() épreuves à effectuer pour passer d’une situation résultant de la réalisation de
épreuves à effectuer pour passer d’une situation résultant de la réalisation de ![]() à une situation où l’on doit avoir
à une situation où l’on doit avoir ![]() .
.
E. Indépendance en probabilités en Maths Sup
1.Indépendance de deux événements en Maths Sup
![]() En utilisant la définition :
En utilisant la définition :
Si ![]() et
et ![]() sont deux événements de
sont deux événements de ![]() ,
, ![]() et
et ![]() sont indépendants ssi
sont indépendants ssi
![]()
![]() En utilisant la propriété :
En utilisant la propriété :
Si ![]() et
et ![]() sont deux événements indépendants de
sont deux événements indépendants de ![]()
![]()
![]() et
et ![]() sont indépendants
sont indépendants
![]()
![]() et
et ![]() sont indépendants
sont indépendants
![]()
![]() et
et ![]() sont indépendants.
sont indépendants.
![]() Si l’on suppose
Si l’on suppose ![]() ,
,
![]() et
et ![]() sont indépendants ssi
sont indépendants ssi
![]()
2. Indépendance mutuelle de  événements en Maths Sup
événements en Maths Sup
![]() Les
Les ![]() événements
événements ![]() forment une famille d’événements mutuellement indépendants lorsque pour toute partie
forment une famille d’événements mutuellement indépendants lorsque pour toute partie ![]() de
de ![]() d’au moins 2 éléments,
d’au moins 2 éléments,
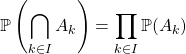 .
.
![]() Écrire les conditions donnant l’indépendance des événements
Écrire les conditions donnant l’indépendance des événements ![]() .
.
![]() P1 : Si
P1 : Si ![]() et si les événements
et si les événements ![]() sont mutuellement indépendants,
sont mutuellement indépendants,
![]() toute sous-famille est une famille d’événements mutuellement indépendants.
toute sous-famille est une famille d’événements mutuellement indépendants.
![]() ils sont 2 à 2 indépendants, mais la réciproque est fausse.
ils sont 2 à 2 indépendants, mais la réciproque est fausse.
![]() P2 : On suppose que les
P2 : On suppose que les ![]() événements
événements ![]() sont mutuellement indépendants, on note pour tout
sont mutuellement indépendants, on note pour tout ![]() ,
, ![]() ou
ou ![]() , les événements
, les événements ![]() sont mutuellement indépendants.
sont mutuellement indépendants.
3. Modèle binomial en probabilités en Maths Sup
Le résultat à connaître : on réalise dans les mêmes conditions ![]() épreuves aléatoires indépendantes donnant lieu chacune à la réalisation d’un même événement
épreuves aléatoires indépendantes donnant lieu chacune à la réalisation d’un même événement ![]() avec une probabilité égale à
avec une probabilité égale à ![]() .
.
La probabilité d’obtenir ![]() réalisations de
réalisations de ![]() au cours de ces
au cours de ces ![]() épreuves est égale à
épreuves est égale à ![]() lorsque
lorsque ![]() .
.
Les meilleures écoles d’ingénieurs du classement recrutent les étudiants qui ont un très bon niveau dans l’ensemble des matières mais particulièrement en maths. Il faut donc être très vigilant à ne faire aucune impasse sur les chapitres au programme de Maths Sup. Pour aider les étudiants dans leurs révision, les cours en ligne sont des ressources facilement accessibles et qui permettent une progression réelle. Quelques idées de chapitres de Maths que les étudiants peuvent travailler en MPSI, PTSI et PCSI :

