Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours de Maths Sup sur les séries numériques en MPSI, MP2I, PTSI, PCSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Être à jour dans ses cours de maths en Maths Sup est fondamental pour réussir les concours, surtout si l’on souhaite être admis dans les meilleures écoles d’ingénieurs françaises. Des révisions régulières, une bonne méthode de travail et des cours particuliers de maths sont les clés de la réussite, les mathématiques étant la matière avec le plus fort coefficient aux concours, aucune impasse ne sera excusée.
A. Définitions des séries numériques en Maths Sup
D1 : À toute suite numérique ![]() , on associe la suite
, on associe la suite ![]() où pour tout
où pour tout ![]() de
de ![]() ,
, 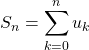 .
.
![]() est la
est la ![]() -ème somme partielle de la série de terme général
-ème somme partielle de la série de terme général ![]() .
.
![]() La série de terme général
La série de terme général ![]() est notée
est notée
![]() ou
ou ![]() .
.
![]() La série
La série ![]() converge (ou est convergente) lorsque la suite
converge (ou est convergente) lorsque la suite ![]() des sommes partielles converge.
des sommes partielles converge.
Dans ce cas, la limite de la suite ![]() est appelée somme de la série et notée
est appelée somme de la série et notée ![]() .
.
![]() Si la suite
Si la suite ![]() diverge, on dit que la série est divergente.
diverge, on dit que la série est divergente.
![]() On définit le reste d’ordre
On définit le reste d’ordre ![]() de la série convergente de terme général
de la série convergente de terme général ![]() par
par 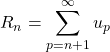 .
.
La suite ![]() converge vers 0.
converge vers 0.
Attention aux notations !
a) ![]() représente un réel ou un complexe.
représente un réel ou un complexe.
b) ![]() ou
ou ![]() , à la rigueur
, à la rigueur ![]() représente la suite réelle ou complexe de terme général
représente la suite réelle ou complexe de terme général ![]() .
.
Il est indispensable de ne pas oublier les parenthèses pour parler de la suite.
c) ![]() ou
ou ![]() est une abréviation pour « la série de terme général
est une abréviation pour « la série de terme général ![]() «
«
Cette notation ne peut intervenir dans une égalité ou une inégalité.
d) ![]() est la somme de la série convergente de terme général
est la somme de la série convergente de terme général ![]() .
.
C’est un scalaire qui peut intervenir dans une égalité ou une inégalité.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
B. Propriétés des séries numériques en Maths Sup
P1 : Si la série ![]() converge, la suite
converge, la suite ![]() converge vers 0.
converge vers 0.
Si la suite ![]() ne converge pas vers 0, on dit que la série de terme général
ne converge pas vers 0, on dit que la série de terme général ![]() diverge grossièrement.
diverge grossièrement.
P2 : Si les séries de termes généraux ![]() et
et ![]() convergent, il en est de même de la série de terme général
convergent, il en est de même de la série de terme général ![]() et de la série de terme général
et de la série de terme général ![]() (où
(où ![]() est un scalaire) et
est un scalaire) et
![]()
![]() .
.
P3 : Soit ![]() une suite complexe,
une suite complexe, ![]() converge si, et seulement si,
converge si, et seulement si, ![]() et
et ![]() convergent.
convergent.
Dans ce cas,
![]()
et 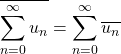 .
.
P4 : Comparaison suite-série.
La suite ![]() est convergente ssi la série de terme général
est convergente ssi la série de terme général ![]() est convergente.
est convergente.
Dans ce cas, ![]() .
.
P5 : Soit ![]() une série réelle ou complexe.
une série réelle ou complexe.
Si la série de terme général ![]() est convergente, on dit que la série de terme général
est convergente, on dit que la série de terme général ![]() est absolument convergente.
est absolument convergente.
Si la série de terme général ![]() est absolument convergente, elle est convergente et de plus :
est absolument convergente, elle est convergente et de plus :
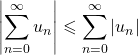 .
.
C. Étude de la convergence des séries de réels positifs ou nuls
P6 : On suppose que pour tout ![]() ,
, ![]()
a) La série de terme général ![]() est convergente si, et seulement si, il existe
est convergente si, et seulement si, il existe
![]() ,
, ![]() ,
, 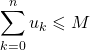 .
.
Dans ce cas, ![]() où
où 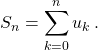
b) Si la série de terme général ![]() positif ou nul diverge,
positif ou nul diverge,
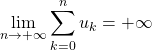 .
.
P7 : On suppose que ![]() et
et ![]() sont deux suites réelles telles qu’il existe
sont deux suites réelles telles qu’il existe ![]() que si
que si ![]() ,
, ![]() .
.
Si ![]() converge,
converge, ![]() converge.
converge.
Dans ce cas, 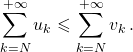
P8 : Soient ![]() et
et ![]() deux suites de réels strictement positifs à partir d’un certain rang telles que
deux suites de réels strictement positifs à partir d’un certain rang telles que ![]() .
.
La série de terme général ![]() converge si, et seulement si, la série de terme général
converge si, et seulement si, la série de terme général ![]() converge.
converge.
P9 : Comparaison série-intégrale
Soit ![]() et
et ![]() une fonction continue, décroissante sur
une fonction continue, décroissante sur ![]() à valeurs dans
à valeurs dans ![]() .
.
On note si ![]() et
et ![]() ,
, ![]()
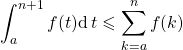
![]()
Ce qui permet de démontrer le résultat au programme de deuxième année :
La série de terme général ![]() converge si, et seulement si, la suite
converge si, et seulement si, la suite
![]() converge.
converge.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
D. Séries absolument convergentes en Maths Sup
P10 : Soit ![]() une suite de réels positifs ou nuls et
une suite de réels positifs ou nuls et ![]() une suite complexe telles que
une suite complexe telles que ![]()
c’est-à-dire il existe ![]() et
et ![]() tels que si
tels que si ![]() ,
, ![]() .
.
Si ![]() converge,
converge, ![]() converge absolument.
converge absolument.
P11 : a) Soit une suite ![]() réelle ou complexe, telle qu’il existe
réelle ou complexe, telle qu’il existe ![]() telle que
telle que
![]() ,
,
alors ![]() converge absolument.
converge absolument.
b) Soit une suite ![]() réelle à termes positifs pour
réelle à termes positifs pour ![]() telle qu’il existe
telle qu’il existe
![]() tel que
tel que ![]() alors
alors ![]() diverge.
diverge.
E. Développement décimal d’un réel positif en Maths Sup
Développement décimal d’un réel positif
Si ![]() , il existe une unique suite
, il existe une unique suite ![]() telle que
telle que
![]()
![]()
![]()
![]() ,
,
![]() La suite n’est pas stationnaire égale à 9
La suite n’est pas stationnaire égale à 9
![]() et
et 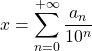
Propriétés d’un développement décimal d’un réel positif
![]() Si
Si ![]() ,
, ![]() est la
est la ![]() -ième décimale de
-ième décimale de ![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]()
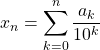 est la valeur approchée de
est la valeur approchée de ![]() à
à ![]() près par défaut
près par défaut
![]()
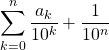 est la valeur approchée de
est la valeur approchée de ![]() à
à ![]() près par excès.
près par excès.
Réviser ses cours et progresser en maths en MPSI, PTSI et PCSI avec uniquement les supports donnés en cours n’est pas toujours suffisant pour les étudiants. Grâce aux cours en ligne, ils bénéficient de nouvelles ressources leur permettant de progresser davantage. De multiples chapitres peuvent ainsi être revus, comme les chapitres suivants :

