Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Sommes et produits en Maths Sup
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en Maths Sup
Ce récapitulatif de cours sur les sommes et produits en maths sup est une ressource essentielle qui vous accompagnera tout au long de votre parcours en classes préparatoires. Il revêt une importance capitale de bien assimiler ces notions et de les maîtriser de manière approfondie. N’hésitez pas à solliciter l’aide d’un prof particulier en maths si vous éprouvez le moindre besoin.
Résumé de cours et méthodes – sommes et produits
1. Coefficients du binôme
1. Définition : Soit ![]() .
.
Si ![]()
![]()
se lit ![]() parmi
parmi ![]() .
.
C’est le nombre de parties à ![]() éléments d’un ensemble
éléments d’un ensemble ![]() contenant
contenant ![]() éléments.
éléments.
2. Valeurs particulières
Pour ![]() et
et ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Dans la suite, ![]() .
.
3. Si ![]() ,
, ![]() .
.
4. Si ![]() ,
, ![]() .
.
5. Formule du triangle de Pascal
Si ![]() ,
, ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Notations  et
et 
2.1. Définitions
![]() def : Soient
def : Soient ![]() et
et ![]() deux entiers tels que
deux entiers tels que ![]() et
et ![]() des complexes, on note
des complexes, on note
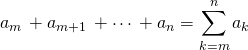
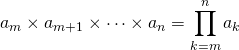
👍 : l’indice de sommation (ou de produit) ![]() peut être remplacé par un indice différent de
peut être remplacé par un indice différent de ![]() et
et ![]() .
.
![]() def : Soient
def : Soient ![]() ,
, ![]() et
et ![]() deux entiers tels que
deux entiers tels que ![]() et
et ![]() des complexes.
des complexes.
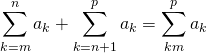
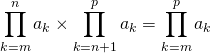
![]() Soient
Soient ![]() et
et ![]() deux entiers tels que
deux entiers tels que ![]() et
et ![]() et
et ![]() deux familles de complexes
deux familles de complexes
![]() P1 :
P1 :
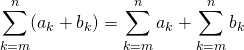
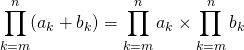
![]() P2 : si
P2 : si ![]() et
et ![]()
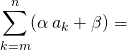
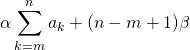 .
.
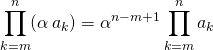 .
.
![]() P3 : Si
P3 : Si ![]() ,
, 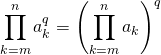
👍 Conseil : il faut savoir utiliser la notation ![]() ou la notation
ou la notation ![]() bien plus précises que les notations utilisant des »
bien plus précises que les notations utilisant des » ![]() « .
« .
2.2. Changement d’indices
Si ![]() et
et ![]() deux entiers tels que
deux entiers tels que ![]() et si
et si ![]() , les
, les ![]() étant des complexes
étant des complexes
![]()
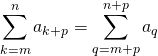
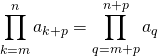
(on a posé ![]() ).
).
![]()
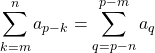
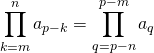
(on a posé ![]() ).
).
⚠️ : Les seuls changements d’indices possibles (![]() étant l’ancien indice et
étant l’ancien indice et ![]() le nouvel indice) sont de la forme
le nouvel indice) sont de la forme ![]() ou
ou ![]() où
où ![]() est un entier.
est un entier.
2.3. Télescopage
Quand il s’agit de calculer
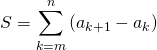 ,
,
on écrit 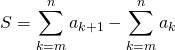
puis en posant ![]() dans la première somme :
dans la première somme :
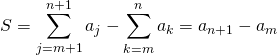 .
.
⚠️ Il faut savoir faire de même le calcul de 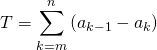 qui donne
qui donne ![]() .
.
2.4.Les sommes à connaître
![]() Formule du binôme de Newton.
Formule du binôme de Newton.
Si ![]() ,
, 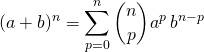
![]() L’identité de Bernoulli
L’identité de Bernoulli
Si ![]() et
et ![]() sont complexes et
sont complexes et ![]()
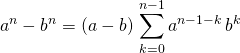
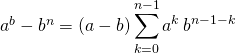 .
.
![]() Suite géométrique
Suite géométrique
Si ![]() et
et ![]() ,
,
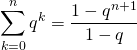 .
.
![]() Si
Si ![]() ,
,
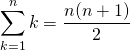
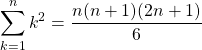
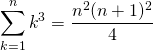 .
.
Démonstrations :
On les établit par récurrence
![]() si
si ![]() ,
,
![]() :
: 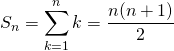 .
.
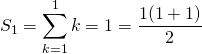 donc
donc ![]() est vraie.
est vraie.
On suppose que ![]() est vraie.
est vraie.
![]()
soit ![]() .
.
On a prouvé ![]() .
.
La formule est vraie par récurrence.
![]() Si
Si ![]() ,
,
![]() :
: 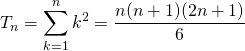
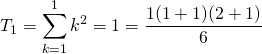 donc
donc ![]() est vraie.
est vraie.
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
soit ![]()
![]()
on obtient :
![]() ce qui prouve
ce qui prouve ![]() .
.
La formule est vraie par récurrence.
![]() Si
Si ![]() ,
,
![]() :
: 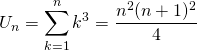
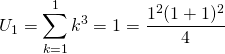 donc
donc ![]() est vraie.
est vraie.
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
soit ![]()
![]() ce qui prouve
ce qui prouve ![]() .
.
La propriété est vraie par récurrence.
Exercice :
Si ![]() et
et ![]() , calculer
, calculer 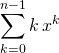
Corrigé :
On introduit si ![]()
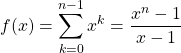
On dérive :
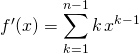
![]()
donc ![]()
et 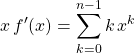
car le terme pour ![]() est nul.
est nul.
On a prouvé que
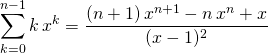 .
.
3.4. Intervertir les signes sommes
![]() les cas sans problèmes
les cas sans problèmes
les bornes de sommation de la somme intérieure ne dépendent pas de l’indice « extérieur » :
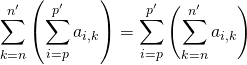
![]() Les cas difficiles
Les cas difficiles
Les bornes de sommation de la somme intérieure dépendent de l’indice « extérieur ».
a) 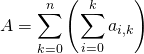
b) 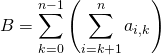 .
.
👍 Il faut seulement retenir la méthode de calcul.
Démonstration du cas difficile :
👍 On rassemble les deux sommes en une seule somme en traduisant simultanément les conditions sur les indices.
![]() Première expression
Première expression
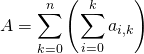
![]()
Puis ![]() étant fixé dans
étant fixé dans ![]() ,
, ![]() doit alors varier de
doit alors varier de ![]() à
à ![]() :
:
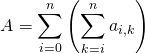 .
.
![]() Deuxième expression
Deuxième expression
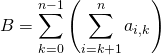
![]()
Puis ![]() étant fixé dans
étant fixé dans ![]() ,
, ![]() doit alors varier de
doit alors varier de ![]() à
à ![]() :
:
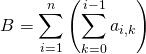 .
.
👍 Bien sûr, vous aurez peut-être à raisonner dans l’autre sens et à transformer
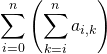 en
en 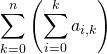
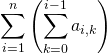 en
en 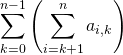
N’hésitez pas à consulter les autres cours en ligne de maths au programme de MPSI, PCSI, PTSI, notamment les chapitres suivants :

