Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Suites numériques en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Suites numériques en Maths Sup
Plan :
1. Les suites récurrentes particulières
2. Cas des suites monotones
3. Cas général
4. Une aide pour les suites de la forme ![]()
5. Suites définies implicitement.
Ce cours en ligne proposé gratuitement par Groupe Réussite vous aidera à comprendre le cours sur les suites en prépa maths sup et à appréhender les méthodes qui vous permettront de résoudre la plupart des exercices. Pour aller plus loin, nous vous proposons sur notre plateforme des professeurs particuliers de maths pour vous aider à travailler et à éliminer les zones d’ombres du cours.
1. Les suites récurrentes particulières en MPSI, PCSI, MP2I et PTSI
1.1. Suites arithmétiques
On suppose que ![]() .
.
D : Les suites arithmétiques sont les suites définies par leur premier terme ![]() et telles qu’il existe
et telles qu’il existe ![]() tel que si
tel que si ![]() .
.
![]() est appelé la raison.
est appelé la raison.
P1 : La suite ![]() arithmétique de raison
arithmétique de raison ![]() vérifie
vérifie ![]() .
.
P2 : Si ![]() est une suite arithmétique et si
est une suite arithmétique et si ![]() ,
,
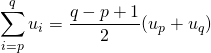 .
.
Cas particulier : 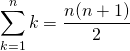
1.2. Suites géométriques
D : Les suites géométriques sont les suites définies par leur premier terme ![]() et telles qu’il existe
et telles qu’il existe ![]() tel que si
tel que si ![]() .
.
![]() est appelé la raison.
est appelé la raison.
P1 : La suite ![]() géométri- que de raison
géométri- que de raison ![]() vérifie
vérifie
![]() .
.
P2 : Si ![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() ,
,
si 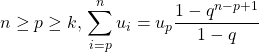 .
.
Cas particulier qu’il est indispensable de connaître par cœur :
si ![]() ,
, ![]() .
.
1.3. Suites arithmético-géométriques
D : Les suites arithmético-géométri- ques sont les suites définies par une relation du type :
il existe ![]() , où
, où ![]() ,
,![]() .
.
Méthode :
On commence par déterminer un complexe ![]() tel que
tel que ![]() .
.
Si ![]() , on note
, on note ![]() .
.
En faisant la soustraction des relations ![]() et
et ![]() , on démontre que la suite
, on démontre que la suite ![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() .
.
On en déduit ![]() où
où ![]() puis on termine par
puis on termine par ![]() .
.
1.4. Suites récurrentes linéaires d’ordre 2
Soit ![]() .
.
On veut déterminer le terme général des suites ![]() vérifiant
vérifiant ![]() .
.
On forme l’équation caractéristique ![]() .
.
![]() 1er cas. L’équation caractéristique admet deux racines distinctes notées
1er cas. L’équation caractéristique admet deux racines distinctes notées ![]() et
et ![]() dans
dans ![]() :
:
il existe ![]()
![]() .
.
![]() 2ème cas. L’équation caractéristique admet une racine double
2ème cas. L’équation caractéristique admet une racine double ![]() :
:
il existe ![]() ,
, ![]() .
.
![]() 3ème cas.
3ème cas. ![]() et l’équation caractéristique admet deux racines complexes conjuguées notées
et l’équation caractéristique admet deux racines complexes conjuguées notées
![]() et
et ![]() :
:
il existe ![]()
![]()
![]() .
.
En général, on calcule les constantes ![]() et
et ![]() en utilisant les valeurs de
en utilisant les valeurs de ![]() et
et ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Étudier la convergence d’une suite monotone
2.1. Des conseils
![]() a) Quand la suite est donnée par récurrence : penser à vérifier qu’elle est bien définie.
a) Quand la suite est donnée par récurrence : penser à vérifier qu’elle est bien définie.
![]() b) Il vaut mieux étudier la monotonie d’une suite
b) Il vaut mieux étudier la monotonie d’une suite ![]() en étudiant le signe de
en étudiant le signe de ![]() .
.
Si vous voulez absolument raisonner avec le quotient, vous devez commen- cer par dire que pour tout ![]() et démontrer que
et démontrer que
… ![]() pour tout
pour tout ![]() pour prouver que
pour prouver que ![]() est croissante
est croissante
… ![]() pour tout
pour tout ![]() pour prouver que
pour prouver que ![]() est décroissante
est décroissante
![]() c) Pour traduire que la suite réelle
c) Pour traduire que la suite réelle ![]() est majorée :
est majorée :
on écrit qu’il existe ![]() tel que pour tout
tel que pour tout ![]()
à respecter l’ordre des quantificateurs mathématiques ;
![]() .
.
s’il existe ![]() tel que
tel que ![]() soit majorée, la suite
soit majorée, la suite ![]() est majorée.
est majorée.
![]() d) Pour traduire que la suite réelle
d) Pour traduire que la suite réelle ![]() est minorée :
est minorée :
on écrit qu’il existe ![]() tel que pour tout
tel que pour tout ![]() .
.
à respecter l’ordre des quantificateurs :
![]() .
.
![]() e) Pour traduire que la suite réelle ou complexe
e) Pour traduire que la suite réelle ou complexe ![]() est bornée, on écrit qu’il existe
est bornée, on écrit qu’il existe ![]() tel que pour tout
tel que pour tout
![]() .
.
à respecter l’ordre des quantifica- teurs :
![]() .
.
Pour une suite réelle, il est nettement plus simple d’utiliser cette caractérisation que d’écrire qu’elle est majorée et minorée.
![]() f) Pour l’étude d’une suite de terme général
f) Pour l’étude d’une suite de terme général ![]() où
où ![]() , écrire
, écrire
![]() et déterminer la limite de la suite
et déterminer la limite de la suite ![]() .
.
Dans le cas où
![]() et
et![]() ,
,
on a une forme indéterminée.
2.2. Suite croissante
Le résultat :
Si ![]() est croissante,
est croissante, ![]() est convergente ssi elle est majorée
est convergente ssi elle est majorée
![]() Si elle est majorée, elle converge vers
Si elle est majorée, elle converge vers ![]() .
.
![]() Si elle n’est pas majorée, elle diverge vers
Si elle n’est pas majorée, elle diverge vers ![]() .
.
![]() M1. Si
M1. Si ![]() est croissante, pour démontrer qu’elle converge, il suffit de prouver qu’elle est majorée.
est croissante, pour démontrer qu’elle converge, il suffit de prouver qu’elle est majorée.
![]() M2. Pour trouver un majorant d’une suite croissante, on peut chercher quelle peut être la limite
M2. Pour trouver un majorant d’une suite croissante, on peut chercher quelle peut être la limite ![]() de la suite et démontrer que
de la suite et démontrer que
pour tout ![]() de
de ![]() ,
, ![]() .
.
![]() M3. Pour démontrer qu’une suite croissante diverge vers
M3. Pour démontrer qu’une suite croissante diverge vers ![]() , on peut supposer qu’elle converge et montrer qu’il y a une contradiction (par exemple en prouvant qu’elle devrait converger vers un nombre
, on peut supposer qu’elle converge et montrer qu’il y a une contradiction (par exemple en prouvant qu’elle devrait converger vers un nombre ![]() puisque la limite d’une suite croissante est sa borne supérieure ).
puisque la limite d’une suite croissante est sa borne supérieure ).
exemple 1
Étude de la suite lorsque ![]() et
et ![]() .
.
Correction : ![]() On démontre facilement par récurren- ce que pour tout
On démontre facilement par récurren- ce que pour tout ![]() ,
, ![]() est défini et
est défini et ![]() .
.
![]()
![]() .
.
Si l’on suppose démontré que ![]() , alors
, alors ![]() et comme la fonction racine carrée est strictement croissante :
et comme la fonction racine carrée est strictement croissante : ![]() .
.
Par récurrence sur ![]() ,
, ![]() . La suite est donc strictement croissante.
. La suite est donc strictement croissante.
![]() Pour deviner un majorant de la suite, on raisonne ainsi :
Pour deviner un majorant de la suite, on raisonne ainsi :
Si la suite ![]() est convergente, elle admet une limite
est convergente, elle admet une limite ![]() (car
(car ![]() ) et vérifiant, en passant à la limite dans la relation
) et vérifiant, en passant à la limite dans la relation ![]() ,
, ![]() soit
soit ![]() , donc
, donc ![]() .
.
![]() On démontre que
On démontre que ![]() est majorée par 2.
est majorée par 2.
Si ![]() , on note
, on note ![]() .
.
![]() est vraie, puisque
est vraie, puisque ![]() .
.
Si elle est vraie au rang ![]() ,
, ![]() , donc
, donc ![]() .
.
![]() La suite est croissante et majorée par
La suite est croissante et majorée par ![]() , elle converge, et on a vu que la seule limite possible était égale à
, elle converge, et on a vu que la seule limite possible était égale à ![]() , elle converge vers 2.
, elle converge vers 2.
exemple 2
Étude de la suite définie par ![]() et
et ![]() .
.
Correction : ![]() , la suite est croissante. Si elle était convergente, elle convergerait vers
, la suite est croissante. Si elle était convergente, elle convergerait vers ![]() tel que
tel que ![]() , donc
, donc ![]() . Mais comme
. Mais comme ![]() , on aboutit à une contradiction.
, on aboutit à une contradiction.
La suite étant croissante, elle diverge vers ![]() .
.
Comme pour tout ![]() , si la suite était convergente, elle convergerait vers
, si la suite était convergente, elle convergerait vers ![]() ce qui est impossible.
ce qui est impossible.
La suite ![]() est croissante et divergente, elle diverge vers
est croissante et divergente, elle diverge vers ![]() .
.
2.3. Suite décroissante
Le résultat :
Si ![]() est décroissante,
est décroissante, ![]() est convergente ssi elle est minorée
est convergente ssi elle est minorée
![]() Si elle est minorée, elle converge vers
Si elle est minorée, elle converge vers ![]() .
.
![]() Si elle n’est pas minorée, elle diverge vers
Si elle n’est pas minorée, elle diverge vers ![]() .
.
![]() M4. Pour trouver un minorant d’une suite décroissante, on peut chercher quelle peut être la limite
M4. Pour trouver un minorant d’une suite décroissante, on peut chercher quelle peut être la limite ![]() de la suite et démontrer que pour tout
de la suite et démontrer que pour tout ![]() de
de ![]() ,
, ![]() .
.
![]() M5. Pour démontrer qu’elle diverge vers
M5. Pour démontrer qu’elle diverge vers ![]() , on peut supposer qu’elle converge et montrer qu’il y a une contradiction (par exemple en prouvant qu’elle devrait converger vers un nombre
, on peut supposer qu’elle converge et montrer qu’il y a une contradiction (par exemple en prouvant qu’elle devrait converger vers un nombre ![]() puisque la limite d’une suite décroissante est sa borne inférieure ).
puisque la limite d’une suite décroissante est sa borne inférieure ).
On a prouvé que ![]() est une surjection de
est une surjection de ![]() sur
sur ![]() .
.
exemple
Étude de la suite définie par
![]()
lorsque ![]() , puis
, puis ![]() .
.
Correction : La suite est décroissante car :
![]() .
.
Pour deviner un minorant de la suite , on raisonne ainsi :
Si la suite ![]() est convergente, elle admet une limite
est convergente, elle admet une limite ![]() vérifiant, en passant à la limite dans la relation
vérifiant, en passant à la limite dans la relation 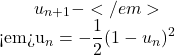 ,
,
![]() soit
soit ![]() .
.
On étudie les deux cas demandés.
![]() Cas
Cas ![]() .
.
Comme la suite est décroissante, pour tout ![]() .
.
Si la suite était minorée, elle converge- rait vers ![]() et
et ![]() ce qui est impossible.
ce qui est impossible.
La suite est décroissante et non minorée, elle diverge vers ![]() .
.
![]() Cas
Cas ![]() .
.
Comme la suite est décroissante, pour tout ![]() .
.
On démontre par récurrence que pour tout ![]() ,
, ![]() .
.
La propriété est vraie pour ![]() .
.
Si elle est vraie au rang ![]() ,
,
![]()
![]()
donc ![]() .
.
La propriété est démontrée par récurrence. Elle est vraie pour tout ![]() .
.
La suite est décroissante et minorée par ![]() , elle converge vers
, elle converge vers ![]() unique limite possible de la suite.
unique limite possible de la suite.
Si ![]() , en utilisant :
, en utilisant :
![]()
on obtient ![]() et d’après le premier cas (en commençant la suite au rang 1), la suite diverge vers
et d’après le premier cas (en commençant la suite au rang 1), la suite diverge vers ![]() .
.
Si la suite ![]() est strictement décroissante et converge vers
est strictement décroissante et converge vers ![]() , pour tout
, pour tout ![]() .
.
Justification : On sait que ![]() ,
,
donc ![]() et
et ![]()
![]() .
.
Retenir l’astuce d’introduire ![]() !
!
2.4. Suites adjacentes
![]() M6. On donne deux suites à étudier : on peut chercher à démontrer qu’elles sont adjacentes.
M6. On donne deux suites à étudier : on peut chercher à démontrer qu’elles sont adjacentes.
On doit prouver que l’une des suites est croissante, l’autre décroissante et que la différence converge vers ![]() .
.
Si les suites ![]() et
et ![]() sont adjacentes, elles convergent vers la même limite
sont adjacentes, elles convergent vers la même limite ![]() qui est encadrée pour tout entier
qui est encadrée pour tout entier ![]() par
par
![]() et
et ![]() .
.
Il est parfois possible d’exprimer la limite commune ![]() .
.
On détermine le signe de ![]() de façon à voir quelle doit être la suite croissante et la suite décroissante.
de façon à voir quelle doit être la suite croissante et la suite décroissante.
Si ![]() , on prouve que
, on prouve que ![]() est décroissante et
est décroissante et ![]() est croissante.
est croissante.
Si ![]() , on prouve que
, on prouve que ![]() est croissante et
est croissante et ![]() est décroissante.
est décroissante.
Un exemple classique
Les relations : pour tout ![]() ,
,
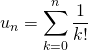 et
et ![]()
définissent des suites adjacentes de limite irrationnelle.
Démonstration : ![]() Convergence des suites
Convergence des suites
![]() Il est évident que
Il est évident que ![]()
![]() Si
Si ![]() . La suite
. La suite ![]() est strictement croissante.
est strictement croissante.
![]() Si
Si ![]()
![]()
![]() .
.
![]()
![]()
![]()
La suite ![]() est strictement décroissante.
est strictement décroissante.
Les suites ![]() et
et ![]() sont adjacentes, elles convergent vers la même limite
sont adjacentes, elles convergent vers la même limite ![]() , de plus
, de plus ![]() donne
donne ![]() .
.
![]() La limite
La limite ![]() est irrationnelle.
est irrationnelle.
Pour tout ![]() ,
,
donc ![]() donne
donne ![]() .
.
On raisonne par l’absurde et on suppose que ![]() . Il existe donc
. Il existe donc ![]() tel que
tel que ![]() .
.
On vient de prouver que ![]() .
.
En multipliant par ![]()
![]() .
.
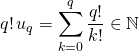
car si ![]()
![]()
![]() est l’entier consécutif à
est l’entier consécutif à ![]() .
.
![]() est un entier strictement compris entre deux entiers consécutifs, on aboutit à une contradiction.
est un entier strictement compris entre deux entiers consécutifs, on aboutit à une contradiction.
La limite ![]() est irrationnelle.
est irrationnelle.
On démontrera ultérieurement que ![]() .
.
![]() M7. Dans certains cas, on parvient à démontrer que pour tout
M7. Dans certains cas, on parvient à démontrer que pour tout ![]() ,
, ![]() , avec
, avec ![]() croissante et
croissante et
![]() décroissante, sans parvenir à prouver que la suite
décroissante, sans parvenir à prouver que la suite ![]() converge vers
converge vers ![]() .
.
On démontre qu’alors la suite ![]() est majorée par
est majorée par ![]() (puisque pour tout
(puisque pour tout ![]() ) et que la suite
) et que la suite
![]() est minorée par
est minorée par ![]() (puisque pour tout
(puisque pour tout ![]() ,
, ![]() ).
).
Elles sont toutes deux convergentes. On peut éventuellement chercher à démontrer que les limites des deux suites sont égales.
3. Convergence de suites dans le cas général en MPSI, MP2I, PCSI et PTSI
3.1. En utilisant les théorèmes sur les convergences
Il n’est pas toujours indispensable d’étudier la monotonie d’une suite pour en justifier la convergence (ou la divergence).
![]() M1 : La somme, le produit de deux suites convergentes sont des suites convergentes et
M1 : La somme, le produit de deux suites convergentes sont des suites convergentes et
![]() Somme de deux suites convergentes
Somme de deux suites convergentes
![]()
![]() Produit de deux suites convergentes
Produit de deux suites convergentes
![]()
![]() Produit d’une suite convergente par
Produit d’une suite convergente par ![]() ,
, ![]() .
.
![]() M2 : Si les suites
M2 : Si les suites ![]() et
et ![]() convergent respectivement vers
convergent respectivement vers ![]() et
et ![]() avec
avec ![]() , il existe un entier
, il existe un entier ![]() tel que si
tel que si ![]() et la suite
et la suite ![]() converge vers
converge vers ![]() .
.
![]() M3 : Si la suite
M3 : Si la suite ![]() diverge vers
diverge vers ![]() (resp.
(resp. ![]() ), il existe un entier
), il existe un entier ![]() tel que si
tel que si ![]() et la suite
et la suite ![]() converge vers
converge vers ![]() .
.
![]() M4 : Si la suite
M4 : Si la suite ![]() converge vers
converge vers ![]() et s’il existe un entier
et s’il existe un entier ![]() tel que si
tel que si ![]() (resp.
(resp. ![]() ),
),
la suite ![]() diverge vers
diverge vers ![]() (resp. vers
(resp. vers ![]() ).
).
![]() M5 : Si la fonction
M5 : Si la fonction ![]() est continue en
est continue en ![]() et si la suite
et si la suite ![]() de
de ![]() converge vers
converge vers ![]() ,
, ![]() .
.
3.2. Utiliser des inégalités
![]() M1. Pour démontrer que la suite
M1. Pour démontrer que la suite ![]() converge vers 0, il suffit de prouver que
converge vers 0, il suffit de prouver que ![]() converge vers 0.
converge vers 0.
![]() M2. Si
M2. Si ![]() et
et ![]() , alors la suite
, alors la suite ![]() diverge vers
diverge vers ![]() .
.
![]() M3. Si
M3. Si ![]() et
et ![]() , alors la suite
, alors la suite ![]() diverge vers
diverge vers ![]() .
.
![]() M4. Théorème d’encadrement
M4. Théorème d’encadrement
Si ![]() et si les suites
et si les suites ![]() et
et ![]() convergent vers la même limite
convergent vers la même limite ![]() , alors
, alors ![]() .
.
Conseil : éviter tout nom « exotique » pour désigner le théorème d’encadre- ment.
![]() M5.
M5. ![]() où la suite
où la suite ![]() est bornée et la suite
est bornée et la suite ![]() converge vers 0, alors la suite
converge vers 0, alors la suite ![]() converge vers 0.
converge vers 0.
![]() M6. S’il existe
M6. S’il existe ![]() et
et ![]() tels que pour tout
tels que pour tout ![]() ,
, ![]() ,
,
on démontre que pour tout ![]() ,
, ![]()
puis comme ![]() , la suite
, la suite ![]() converge vers
converge vers ![]() et par encadrement la suite
et par encadrement la suite ![]() converge vers
converge vers ![]() .
.
3.3. En utilisant les suites extraites
![]() M1 : Si la suite
M1 : Si la suite ![]() converge vers
converge vers ![]() , toute suite extraite
, toute suite extraite ![]() converge vers
converge vers ![]() .
.
(On rappelle que ![]() est une fonction strictement croissante de
est une fonction strictement croissante de ![]() dans
dans ![]() ).
).
![]() M2. Si l’on trouve deux suites extraites de
M2. Si l’on trouve deux suites extraites de ![]() qui admettent des limites différentes, la suite
qui admettent des limites différentes, la suite ![]() diverge.
diverge.
![]() M3. Pour montrer que
M3. Pour montrer que ![]() converge vers
converge vers ![]() , il suffit de prouver que
, il suffit de prouver que ![]() et
et
![]() .
.
![]() M4 : Théorème de Bolzano Weierstrass.
M4 : Théorème de Bolzano Weierstrass.
Si la suite ![]() réelle ou complexe est bornée, il existe une suite extraite convergente.
réelle ou complexe est bornée, il existe une suite extraite convergente.
3.4. Cas des suites complexes
![]() M1. Pour prouver qu’une suite complexe
M1. Pour prouver qu’une suite complexe ![]() converge, on peut
converge, on peut
démontrer que les suites ![]() et
et ![]() où
où ![]() et
et ![]() convergent.
convergent.
Dans ce cas,
![]() .
.
![]() M2. On peut chercher le module
M2. On peut chercher le module ![]() de
de ![]() et un argument
et un argument ![]() de
de ![]() .
.
Si l’on peut démontrer que ![]() converge vers
converge vers ![]() et
et ![]() converge vers
converge vers ![]() , en écrivant
, en écrivant ![]() ,
,
![]() et
et ![]() convergent vers
convergent vers ![]() et
et ![]() respectivement,
respectivement,
donc la suite ![]() converge vers
converge vers ![]() .
.
3.5. Sommes de suites qui convergent vers 0
On suppose dans ce paragraphe que 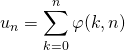 .
.
il est interdit de faire la somme des limites puisqu’il ne s’agit pas d’une somme d’un nombre fixé de suites.
![]() M1. On peut chercher quel est le plus petit des termes et le plus grand des termes
M1. On peut chercher quel est le plus petit des termes et le plus grand des termes ![]() et encadrer
et encadrer ![]() entre deux suites. On pourra conclure si les deux suites qui encadrent
entre deux suites. On pourra conclure si les deux suites qui encadrent ![]() ont même limite.
ont même limite.
Par contre si ![]() est un entier fixé,
est un entier fixé,
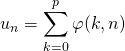 est la somme de
est la somme de ![]() suites, il suffit de chercher la limite de la suite
suites, il suffit de chercher la limite de la suite ![]() pour
pour ![]() .
.
exemple 1
Étude de la suite définie pour ![]() par
par 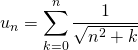 .
.
Correction :
Comme pour tout ![]() entre
entre ![]() et
et ![]() ,
, ![]()
![]()
donc ![]()
puis par somme, ![]() , par encadrement entre deux suites qui convergent vers
, par encadrement entre deux suites qui convergent vers
![]() , la suite
, la suite ![]() converge vers
converge vers ![]() .
.
Par contre :
si ![]() ,
, 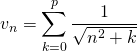 ,
,
![]() est la somme de
est la somme de ![]() (fixé) termes qui convergent tous vers
(fixé) termes qui convergent tous vers ![]() . Donc la suite
. Donc la suite ![]() converge vers
converge vers ![]() .
.
exemple 2
La suite de terme général 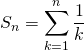 diverge vers
diverge vers ![]()
Correction :
C’est une suite croissante : ![]() .
.
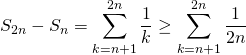
![]() .
.
Si la suite ![]() convergeait vers
convergeait vers ![]() , on aurait en passant à la limite
, on aurait en passant à la limite ![]() , ce qui est impossible.
, ce qui est impossible.
La suite croissante est divergente, elle diverge vers ![]() .
.
![]() M2. Deuxième période. Reconnaître une somme de Riemann.
M2. Deuxième période. Reconnaître une somme de Riemann.
Si ![]() est une fonction continue sur
est une fonction continue sur ![]() à valeurs dans
à valeurs dans ![]() , on note pour
, on note pour ![]() ,
,
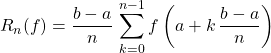
et 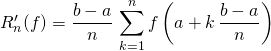
les sommes de Riemann d’ordre ![]() associées à la fonction
associées à la fonction ![]() .
.
![]() .
.
![]() .
.
👍 En général ![]() et il suffira de reconnaitre :
et il suffira de reconnaitre :
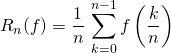
ou 
qui sont les termes généraux de deux suites qui convergent vers ![]() .
.
exemple 3
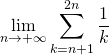
Correction : En posant ![]() ,
,
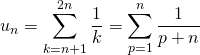
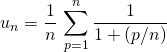 .
.
On note ![]() .
.
![]() est continue sur
est continue sur ![]() .
.
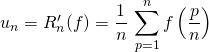
donc ![]()
![]() .
.
3.6. En désespoir de cause
La démonstration de la convergence d’une suite par les « ![]() » et «
» et « ![]() » doit être réservée aux cas » théoriques » quand on a épuisé toutes les autres pistes
» doit être réservée aux cas » théoriques » quand on a épuisé toutes les autres pistes
(un exemple de situation où il faut utiliser les « ![]() » et «
» et « ![]() » : démonstration de la moyenne de Cesaro) .
» : démonstration de la moyenne de Cesaro) .
Rappels :
![]() La suite
La suite ![]() converge vers
converge vers ![]() ssi
ssi
![]()
![]() .
.
![]() La suite
La suite ![]() diverge vers
diverge vers ![]() ssi
ssi
![]()
![]() .
.
![]() La suite
La suite ![]() diverge vers
diverge vers ![]() ssi
ssi
![]()
![]() .
.
⚠️ Il faut aussi savoir faire la négation des trois affirmations précédentes.
![]() La suite
La suite ![]() ne converge pas vers
ne converge pas vers ![]() ssi
ssi ![]()
![]() .
.
![]() La suite
La suite ![]() ne diverge pas vers
ne diverge pas vers ![]() ssi
ssi ![]()
![]() .
.
![]() La suite
La suite ![]() ne diverge pas vers
ne diverge pas vers ![]() ssi
ssi ![]()
![]() .
.
⚠️ Savoir redémontrer les propriétés suivantes :
![]() Si la suite
Si la suite ![]() converge vers
converge vers ![]() ,
,
![]() .
.
![]() Si la suite
Si la suite ![]() converge vers
converge vers ![]() ,
,
![]() .
.
Démonstration : ![]() Si la suite
Si la suite ![]() converge vers
converge vers ![]() , on traduit cette limite en prenant
, on traduit cette limite en prenant ![]() ,
,
![]()
donc ![]()
![]() .
.
![]() Si la suite
Si la suite ![]() converge vers
converge vers ![]() , on applique le premier résultat à la suite
, on applique le premier résultat à la suite ![]() qui converge vers
qui converge vers ![]() , donc
, donc ![]() .
.
On termine en multipliant l’inégalité par ![]() .
.
4. Une aide pour les suites 
⚠️ Il n’y a aucun résultat au program- me, il faudra donner des explications complètes.
On suppose dans cette partie que ![]() est continue sur l’intervalle
est continue sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() (on dit que
(on dit que ![]() est un intervalle
est un intervalle ![]() -stable).
-stable).
Par démonstration par récurrence, on démontre que pour tout ![]() ,
, ![]() .
.
Les racines de ![]() sont appelées points fixes de
sont appelées points fixes de ![]() .
.
👍 On peut s’aider d’un dessin précis.
On représente le graphe de ![]() et la droite
et la droite ![]() d’équation
d’équation ![]() .
.
On se donne ![]() , on en déduit le point
, on en déduit le point ![]() puis en déterminant l’intersection la droite d’équation
puis en déterminant l’intersection la droite d’équation ![]() et
et ![]() , on obtient le point
, on obtient le point ![]() que l’on projette sur
que l’on projette sur ![]() pour obtenir
pour obtenir ![]() .
.
On réitère la construction.
Cela peut donner une idée des démonstrations à effectuer.
4.1. Fonction croissante sur ![]() , intervalle
, intervalle ![]() – stable
– stable
On suppose dans ce paragraphe que ![]() et
et ![]() où
où ![]() est continue et croissante de
est continue et croissante de ![]() dans
dans ![]() .
.
![]() Résultat 1 :
Résultat 1 :
La suite ![]() est monotone, on cherche son sens de variation en utilisant le signe de
est monotone, on cherche son sens de variation en utilisant le signe de ![]() .
.
Démonstration : ![]() Si
Si ![]() , on démontre que
, on démontre que ![]() est vérifiée.
est vérifiée.
![]() est vraie.
est vraie.
Si ![]() est vraie, par croissance de
est vraie, par croissance de ![]() sur
sur ![]() et sachant que l’on raisonne avec des points de
et sachant que l’on raisonne avec des points de ![]()
![]() soit
soit ![]() ,
,
ce qui prouve ![]() .
.
La propriété est démontrée par récurrence.
![]() Si
Si ![]() , on démontre que
, on démontre que ![]() est vérifiée.
est vérifiée.
![]() est vraie.
est vraie.
Si ![]() est vraie, par croissance de
est vraie, par croissance de ![]() sur
sur ![]() et sachant que l’on raisonne avec des points de
et sachant que l’on raisonne avec des points de ![]()
![]() soit
soit ![]() ,
,
ce qui prouve ![]() .
.
La propriété est démontrée par récurrence.
![]() Suite du raisonnement :
Suite du raisonnement :
On introduit la fonction ![]() .
.
Si ![]() s’annule sur
s’annule sur ![]() en
en ![]() , on sera amené à étudier les cas :
, on sera amené à étudier les cas :
![]()
![]() , on démontre que la suite est stationnaire
, on démontre que la suite est stationnaire
![]()
![]() (si cette inégalité est possible)
(si cette inégalité est possible)
![]() il existe
il existe ![]() tel que
tel que ![]()
![]()
![]() (si cette inégalité est possible).
(si cette inégalité est possible).
👍 On commence dans le cas d’une fonction croissante, à donner le tableau de variation de ![]() et le signe de
et le signe de ![]() .
.
Faire apparaître dans le tableau de variation de ![]() les zéros de
les zéros de ![]() .
.
Un exemple d’illustration graphique :

4.2. Fonction décroissante sur ![]() , intervalle
, intervalle ![]() -stable
-stable
On suppose dans ce paragraphe que ![]() et
et ![]() où
où ![]() est continue et décroissante de
est continue et décroissante de ![]() dans
dans ![]() .
.
Si ![]() est un point fixe
est un point fixe ![]() de
de ![]() , la suite est constante égale à
, la suite est constante égale à ![]() .
.
Première méthode
![]() Résultat 1 :
Résultat 1 :
Les suites ![]() et
et ![]() sont monotones et varient en sens contraire. On cherche les sens de variation en utilisant le signe de
sont monotones et varient en sens contraire. On cherche les sens de variation en utilisant le signe de ![]() .
.
![]() Résultat 2 : On cherche les points fixes de
Résultat 2 : On cherche les points fixes de ![]() sur
sur ![]() .
.
👍 Si ![]() est une fonction polynôme, on peut trouver une fonction polynôme
est une fonction polynôme, on peut trouver une fonction polynôme ![]() telle que
telle que ![]()
Puis on étudie la suite ![]() en se plaçant sur un intervalle dont les bornes sont deux points fixes consécutifs de
en se plaçant sur un intervalle dont les bornes sont deux points fixes consécutifs de ![]() , en vérifiant que ces intervalles sont
, en vérifiant que ces intervalles sont ![]() -stables.
-stables.
démonstration résultat 1 : On note ![]() ,
, ![]() est une fonction croissante de
est une fonction croissante de ![]() dans
dans ![]() .
.
La suite ![]() est définie par
est définie par
![]() et
et ![]()
donc elle est monotone.
Puis comme ![]() avec
avec ![]() décroissante, la suite
décroissante, la suite ![]() est monotone et varie en sens contraire de la suite
est monotone et varie en sens contraire de la suite ![]() .
.
Deuxième méthode :
les calculs précédents peuvent être lourds et l’énoncé peut proposer de trouver ![]() tel que
tel que![]() .
.
On utilise ensuite la méthode M6 du paragraphe 3.2.
Un exemple d’illustration graphique :

Il est des cas où l’on sait résoudre alors que la fonction ![]() change de monotonie.
change de monotonie.
Exemple :
Étude de la suite définie par ![]() et
et ![]() où
où ![]() .
.
Correction : On reprend une étude plus systématique de l’exemple 3 du §2.3.
![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
![]() est croissante sur
est croissante sur ![]() et décroissante sur
et décroissante sur ![]() avec
avec ![]() .
.
![]() .
.
On en déduit que la suite ![]() est toujours décroissante et que si la suite converge, elle converge vers
est toujours décroissante et que si la suite converge, elle converge vers ![]() .
.
On remarque que ![]() et
et ![]() .
.
On distingue les cas suivants :
![]()
![]() , la suite est constante égale à 1.
, la suite est constante égale à 1.
![]()
![]() ,
, ![]() , la suite est stationnaire et converge vers
, la suite est stationnaire et converge vers ![]() .
.
![]() Cas
Cas ![]() .
.
L’intervalle ![]() est
est ![]() -stable, la suite
-stable, la suite ![]() est décroissante et
est décroissante et ![]() .
.
Si elle était convergente vers ![]() ,
, ![]() .
.
En utilisant ![]() , à la limite
, à la limite ![]() ce qui est impossible.
ce qui est impossible.
La suite est décroissante et divergente, elle diverge vers ![]() .
.
![]() Cas
Cas ![]() .
.
Attention l’intervalle ![]() n’est pas stable.
n’est pas stable.
Mais ![]() étant strictement décroissante sur
étant strictement décroissante sur ![]() ,
, ![]() donc
donc ![]() . On se ramène au cas précédent à partir du rang 1, la suite
. On se ramène au cas précédent à partir du rang 1, la suite ![]() diverge vers
diverge vers ![]() .
.
![]() Cas
Cas ![]()
En utilisant les variations de ![]() ,
, ![]() ,
,
par récurrence, pour tout ![]() ,
, ![]() .
.
La suite est décroissante et minorée par ![]() , elle converge vers
, elle converge vers ![]() unique limite possible de la suite.
unique limite possible de la suite.
Conclusion
La suite converge vers ![]() lorsque
lorsque ![]() et diverge vers
et diverge vers ![]() sinon.
sinon.
5. Suites définies implicitement
Pour démontrer qu’une équation écrite sous la forme ![]() admet une seule solution
admet une seule solution ![]() dans l’intervalle
dans l’intervalle ![]() et étudier la suite
et étudier la suite ![]() :
:
![]() M1. On démontre que
M1. On démontre que ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() , avec
, avec ![]() (en démontrant que
(en démontrant que ![]() est continue et strictement monotone sur
est continue et strictement monotone sur ![]() ).
).
On obtient ainsi l’existence et l’unicité de ![]() .
.
![]() M2. L’énoncé ne demande pas de justifier la monotonie de la suite mais seulement d’étudier sa convergence.
M2. L’énoncé ne demande pas de justifier la monotonie de la suite mais seulement d’étudier sa convergence.
Pour déterminer la limite de ![]() , écrire l’équation
, écrire l’équation ![]() , de façon à pouvoir passer à la limite dans l’équation ainsi obtenue en raisonnant par des encadrements.
, de façon à pouvoir passer à la limite dans l’équation ainsi obtenue en raisonnant par des encadrements.
![]() M3. L’énoncé demande de justifier la monotonie de la suite.
M3. L’énoncé demande de justifier la monotonie de la suite.
![]() On peut calculer
On peut calculer ![]() en injectant dans cette relation l’équation vérifiée par
en injectant dans cette relation l’équation vérifiée par ![]() (obtenue avec
(obtenue avec ![]() ) et déterminer son signe.
) et déterminer son signe.
Si ![]() est strictement croissante,
est strictement croissante,
… ![]() s’écrit
s’écrit ![]()
et donne ![]()
… ![]() s’écrit
s’écrit ![]()
et donne ![]() .
.
Si ![]() est strictement décroissante,
est strictement décroissante,
… ![]() s’écrit
s’écrit ![]()
et donne ![]()
… ![]() s’écrit
s’écrit ![]()
et donne ![]() .
.
(S’aider si nécessaire d’un tableau de variation). Dans ce cas, on a démontré que la suite ![]() est monotone.
est monotone.
![]() Il reste alors à démontrer selon le cas que
Il reste alors à démontrer selon le cas que ![]() est majorée ou minorée.
est majorée ou minorée.
![]() Pour déterminer la limite de
Pour déterminer la limite de ![]() , écrire l’équation
, écrire l’équation ![]() , de façon à pouvoir passer à la limite dans l’équation ainsi obtenue.
, de façon à pouvoir passer à la limite dans l’équation ainsi obtenue.
exemple 1
Montrer que l’équation ![]()
admet une unique solution ![]() .
.
Démontrer que la suite ![]() converge, trouver sa limite et et celle de
converge, trouver sa limite et et celle de ![]() .
.
Correction : ![]() On note
On note ![]() .
.
![]() est continue et strictement croissan- te sur
est continue et strictement croissan- te sur ![]() ,
, ![]() et
et ![]() .
.
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() , il existe un unique réel
, il existe un unique réel ![]() tel que
tel que ![]() .
.
![]() et
et ![]() donnent
donnent ![]() .
.
![]() En écrivant
En écrivant ![]() avec
avec ![]() ,
, ![]() , par encadrement, la suite
, par encadrement, la suite ![]() converge vers
converge vers ![]() .
.
![]() En écrivant
En écrivant ![]() ,
, ![]() , donc
, donc ![]() .
.
exemple 2.
Soit ![]() . Montrer que l’équation
. Montrer que l’équation ![]()
admet une unique solution ![]() dans
dans ![]()
Trouver le sens de variation de la suite ![]() , montrer qu’elle converge et trouver sa limite.
, montrer qu’elle converge et trouver sa limite.
Correction : On note ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et
et ![]() si
si ![]() .
.
![]() est continue sur
est continue sur ![]() , strictement décroissante ,
, strictement décroissante , ![]() et on démontre que
et on démontre que ![]() en écrivant
en écrivant ![]()
![]()
![]() et
et ![]() est strictement décroissante donc
est strictement décroissante donc ![]() .
.
La suite ![]() est décroissante et minorée par
est décroissante et minorée par ![]() , elle converge. On note
, elle converge. On note ![]() sa limite.
sa limite.
On écrit ![]() .
.
La suite ![]() converge vers
converge vers ![]() et
et ![]() , donc
, donc
![]() .
.
En écrivant ![]() , on obtient
, on obtient ![]() .
.
Ce qui donne ![]() .
.
De nombreux autres cours en ligne dédiés au programme de maths en Maths Sup sont disponibles totalement gratuitement, dont les cours suivants :

