Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les suites numériques en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Limites de suites, constante d’Euler
1. Utilisation des suites récurrentes du programme
2. Des limites de suites simples
3. En utilisant des inégalités
4. Suite définie par une relation de récurrence
5. Suite vérifiant une inégalité
6. Une superposition de racines carrées
7. Constante d’Euler
8. Avec de la trigonométrie
9. La même suite à deux périodes différentes de l’année
10. Deux exercices théoriques
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Utilisation des suites numériques récurrentes du programme
Exercice 1
Déterminer ![]() en fonction de
en fonction de ![]() si
si ![]() .
.
Correction : On note ![]() .
.
La relation implique ![]() .
.
C’est une suite arithmético-géométrique.
On résout ![]() .
.
On forme ![]() .
.
On obtient ![]() .
.
![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() et de premier terme
et de premier terme ![]() .
.
On en déduit que ![]() , donc
, donc ![]() puis
puis
![]() .
.
Exercice 2
Déterminer la suite ![]() sachant que
sachant que ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
Correction : ![]() Il ne faut pas oublier de justifier l’existence de la suite
Il ne faut pas oublier de justifier l’existence de la suite ![]() .
.
👍 On définit le terme d’indice ![]() en fonction des termes d’indices
en fonction des termes d’indices ![]() et
et ![]() , on utilise une hypothèse de récurrence double contenant le résultat aux rangs
, on utilise une hypothèse de récurrence double contenant le résultat aux rangs ![]() et
et ![]() .
.
On note
si ![]() .
.
![]() est vraie par définition de
est vraie par définition de ![]() et
et ![]() .
.
On suppose que ![]() est vraie.
est vraie.
En utilisant ![]() , on en déduit que
, on en déduit que ![]() est défini et
est défini et ![]() .
.
on a donc prouvé que ![]() est vraie.
est vraie.
Par récurrence, on a prouvé que la suite est définie et à valeurs strictement positives.
![]() On note
On note ![]() .
.
La suite ![]() vérifie
vérifie
![]()
soit ![]() .
.
C’est une suite récurrente linéaire d’ordre 2 d’équation caractéristique
![]()
Il existe ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]()
avec ![]() et
et ![]() .
.
On obtient les équations
![]()
![]() ,
, ![]()
alors ![]()
et ![]() .
.
Exercice 3
Déterminer la suite ![]() si
si ![]() et
et ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
Correction : ![]() Il ne faut pas oublier de justifier l’existence de la suite
Il ne faut pas oublier de justifier l’existence de la suite ![]() .
.
On note
si ![]() .
.
![]() est vraie par définition de
est vraie par définition de ![]() et
et ![]() .
.
On suppose que ![]() est vraie.
est vraie.
On en déduit que ![]() est défini et que
est défini et que ![]() .
.
Donc ![]() est vraie.
est vraie.
![]() On peut calculer le
On peut calculer le ![]() de la relation :
de la relation :
![]()
soit en posant ![]() :
:
![]()
c’est une suite récurrente linéaire d’ordre 2, d’équation caractéristique ![]()
On en déduit qu’il existe ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]()
avec ![]() et
et ![]()
ssi ![]() et
et ![]()
alors ![]() ,
, ![]()
![]()
![]() .
.
2. Des limites de suites simples
exercice 1
Pour ![]() . Vers quoi la suite converge ?
. Vers quoi la suite converge ?
Correction : On écrit
![]()
![]()
donc ![]()
Comme ![]()
et ![]() ,
, ![]() .
.
Exercice 2
Pour ![]() . Vers quoi la suite converge-t-elle ?
. Vers quoi la suite converge-t-elle ?
Correction :On démontre que
![]() si
si ![]()
![]() :
:
Soit ![]() ,
, ![]() ,
, ![]() est croissante sur
est croissante sur ![]() avec
avec ![]() donc
donc ![]() .
.
Alors ![]() , donc par encadrement,
, donc par encadrement, ![]() .
.
Exercice 3
Pour ![]()
![]() . Vers quoi la suite converge ?
. Vers quoi la suite converge ?
Correction : En utilisant la quantité conjuguée,
![]()
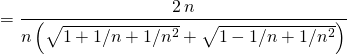
![]()
![]()
Exercice 4
Si ![]() ,
, ![]() . Vers quoi la suite converge ?
. Vers quoi la suite converge ?
Correction : ![]() et
et ![]() .
.
En écrivant ![]()
![]() .
.
![]() et
et ![]()
![]()
Par continuité de la fonction exponentielle, ![]() .
.
Exercice 5
Si ![]() ,
, ![]() . Vers quoi la suite converge ?
. Vers quoi la suite converge ?
Correction : ![]()
en utilisant ![]() ,
,
![]() .
.
Par continuité de la fonction exponentielle, ![]() .
.
![]()
en utilisant ![]() ,
,
![]() .
.
Par continuité de la fonction exponentielle, ![]() .
.
3. Utilisation d’inégalités
Exercice 1 Mines Telecom MP 2018
Nature de la suite de terme général
 . Converge-t-elle ?
. Converge-t-elle ?
Correction : On additionne
![]()
termes compris entre
![]() et
et ![]()
donc ![]()
soit ![]() .
.
Par encadrement par deux suites qui convergent vers ![]() , la suite
, la suite ![]() converge vers
converge vers ![]() .
.
Exercice 2
Soit ![]() de
de ![]() et
et ![]() .
.
Étude de la suite ![]() .
.
Correction : Soit si ![]() .
.
![]() est vraie et
est vraie et ![]() aussi car
aussi car ![]() .
.
On suppose que ![]() est vraie pour un entier
est vraie pour un entier ![]() .
.
Il est évident que ![]()
et ![]() car
car ![]() .
.
Comme la suite ![]() est bornée,
est bornée,
![]()
donc ![]() .
.
La suite ![]() converge vers
converge vers ![]() .
.
Exercice 3
Convergence de la suite ![]() définie par
définie par ![]() et
et ![]()
Correction : Par récurrence simple,
![]() .
.
On écrit la relation de définition sous la forme :
![]()
donc si ![]() ,
, ![]() .
.
La suite ![]() est décroissante et à valeurs positives.
est décroissante et à valeurs positives.
![]() donne
donne ![]() .
.
Par encadrement, ![]() .
.
4. Suites définies par une relation de récurrence
Exercice 1
Soit la suite ![]() définie par
définie par ![]() et pour tout entier
et pour tout entier ![]() ,
, ![]() .
.
Question 1
Montrer que pour tout ![]() ,
, ![]() .
.
Correction : Soit si ![]()
Pour ![]() , donc
, donc ![]() est vérifiée.
est vérifiée.
On suppose que ![]() est vraie :
est vraie :
![]()
donc ![]()
que l’on doit comparer à ![]() .
.
Les réels comparés étant positifs ou nuls, on peut raisonner par équivalence en élevant les termes au carré :
![]()
![]()
![]()
![]()
![]() .
.
On obtient par équivalence une inégalité vérifiée, donc on a prouvé que
![]()
et alors ![]() , ce qui justifie
, ce qui justifie ![]() .
.
La propriété est démontrée par récurrence.
👍 si ![]() et
et ![]() sont deux réels positifs, démontrer que
sont deux réels positifs, démontrer que ![]() revient à démontrer que
revient à démontrer que ![]() .
.
Question 2
Déterminer ![]() .
.
Correction : ![]() ,
,
puis en utilisant l’inégalité de la question 1, ![]() ,
,
par encadrement, ![]() .
.
On a prouvé que ![]() .
.
Question 3
![]() .
.
Correction : Pour lever l’indétermination, on utilise la quantité conjuguée, puis l’on divise numérateur et dénominateur par ![]() et
et ![]() respectivement, pour utiliser la question précédente :
respectivement, pour utiliser la question précédente :
![]()
![]()
![]()
On utilise ensuite
![]()
![]() ,
,
alors ![]() .
.
5. Suite vérifiant une inégalité
Soit ![]() une suite bornée telle que pour tout
une suite bornée telle que pour tout ![]() de
de ![]() ,
, ![]() .
.
Question 1
Soit ![]() où
où ![]() . Montrer que la suite
. Montrer que la suite ![]() est convergente.
est convergente.
Correction : ![]()
![]()
![]() est une suite croissante.
est une suite croissante.
C’est une différence de deux suites bornées, elle est bornée.
![]() est une suite croissante et majorée, elle est convergente.
est une suite croissante et majorée, elle est convergente.
Question 2
En raisonnant par l’absurde, on peut démontrer que la suite ![]() converge vers
converge vers ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : On note ![]() la limite de la suite
la limite de la suite ![]() .
.
![]() On suppose que
On suppose que ![]() .
.
Il existe ![]() si
si ![]() .
.
Soit ![]() ,
, 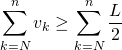
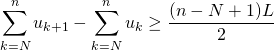
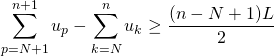
![]()
donne par minoration par une suite qui diverge vers ![]() ,
, ![]()
ce qui contredit le fait que la suite soit bornée.
Il est impossible que ![]() .
.
![]() On suppose que
On suppose que ![]() .
.
Il existe ![]() si
si ![]() .
.
Soit ![]() ,
, 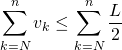
avec un raisonnement analogue au précédent,
![]()
donne par majoration par une suite qui diverge vers ![]() ,
, ![]()
ce qui contredit le fait que la suite soit bornée.
Il est impossible que ![]() .
.
On a donc prouvé que ![]() .
.
Question 3
On peut prouver qu’il existe ![]() tel que
tel que ![]() soit monotone, donc la suite
soit monotone, donc la suite ![]() converge. Vrai ou Faux ?
converge. Vrai ou Faux ?
Correction : La suite ![]() est croissante et converge vers 0, donc
est croissante et converge vers 0, donc ![]() est la borne supérieure de la suite, ce qui donne
est la borne supérieure de la suite, ce qui donne
si ![]() , soit
, soit ![]() .
.
La suite ![]() est décroissante et bornée, elle converge.
est décroissante et bornée, elle converge.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
6. Une superposition de racines carrées
Question 1
Soit ![]() ,
, ![]()
et ![]() ,
, ![]() .
.
On note ![]() .
.
Montrer que ![]() .
.
Étudier la convergence de la suite ![]() .
.
correction : Si ![]() , on note
, on note ![]() .
.
![]() Comme
Comme ![]() ,
,
on a prouvé que ![]() .
.
![]() On suppose que
On suppose que ![]() est vérifiée.
est vérifiée.
La fonction ![]() étant croissante, par
étant croissante, par ![]()
![]() (*)
(*)
![]()
![]()
![]()
![]()
(*) donne ![]() .
.
La propriété est démontrée par récurrence.
![]()
en multipliant par la quantité conjuguée
![]() .
.
Les racines de ![]() sont
sont
![]() et
et ![]() .
.
![]()
avec ![]() car
car ![]()
et ![]() , donc
, donc ![]() .
.
La suite ![]() de réels positifs est croissante et majorée, elle converge vers
de réels positifs est croissante et majorée, elle converge vers ![]() tel que
tel que ![]() (équation obtenue en passant à la limite dans la relation
(équation obtenue en passant à la limite dans la relation ![]() ), ce qui donne
), ce qui donne ![]() , donc
, donc ![]() .
.
Question 2
On suppose toujours ![]() .
.
Soit une suite ![]() telle que
telle que ![]() .
.
On définit pour ![]()
![]()
La suite ![]() converge.
converge.
Vrai ou Faux ?
Correction : ![]() En utilisant
En utilisant ![]() et la croissance de la fonction racine carrée,
et la croissance de la fonction racine carrée,
![]()
puis ![]()
et en réitérant le raisonnement, ![]() .
.
![]() En utilisant
En utilisant ![]() ,
,
![]()
(avec ![]() signes
signes ![]() ) .
) .
On a prouvé que ![]() donc
donc ![]() .
.
La suite ![]() est croissante et majorée, elle est convergente.
est croissante et majorée, elle est convergente.
7. Constante d’Euler
Question 1
Montrer que pour tout ![]() ,
,![]() .
.
Correction : ![]() Soit
Soit ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
![]() est croissante sur
est croissante sur ![]() donc
donc
![]() soit
soit ![]()
![]() .
.
![]() Soit
Soit ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et
et ![]()
![]() est croissante sur
est croissante sur ![]() donc
donc
![]() soit
soit ![]()
![]() .
.
Question 2.
Montrer que la suite de terme général 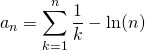 converge.
converge.
On notera ![]() sa limite que l’on ne cherchera pas à calculer.
sa limite que l’on ne cherchera pas à calculer.
Correction : ![]() Monotonie
Monotonie ![]()
![]()
En utilisant la question 1 pour ![]()
![]()
soit ![]()
donc ![]() .
.
La suite ![]() est décroissante.
est décroissante.
![]() En utilisant la première question,
En utilisant la première question,
pour tout ![]()
donc par somme,
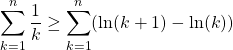
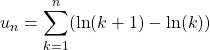
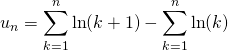
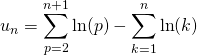
![]()
donc 
et ![]() .
.
La suite ![]() est décroissante et minorée par 0, elle converge vers un réel
est décroissante et minorée par 0, elle converge vers un réel ![]() appelé constante d’Euler.
appelé constante d’Euler.
![]() .
.
Question 3
Déterminer la limite de la suite de terme général 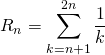
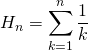 , donc
, donc donc
On note
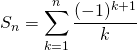 .
.Montrer que la suite
Correction : 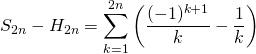
si ![]()
si ![]()
Il ne subsiste que les termes lorsque ![]() avec
avec ![]() ,
,
donc 
soit ![]()
donc ![]()
et ![]() .
.
Comme ![]() ,
,
![]() .
.
Par propriété des suites extraites, ![]() .
.
Question 5
On suppose que la suite ![]() est définie par
est définie par ![]() et
et ![]() .
.
Si ![]() , exprimer
, exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() .
.
En déduire une CNS pour que la suite ![]() converge.
converge.
Question 6
Étude de la convergence des suites ![]() et
et ![]() définies par leurs premiers termes
définies par leurs premiers termes ![]() et
et ![]() et les relations
et les relations
![]()
![]() .
.
8. Avec de la trigonométrie
Soit ![]() et si
et si ![]() ,
, 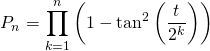 .
.
Justifier l’existence de ![]() , démontrer que la suite converge et trouver sa limite.
, démontrer que la suite converge et trouver sa limite.
Correction : ![]()
![]() donc
donc ![]() est défini.
est défini.
![]() On suppose dans la suite que
On suppose dans la suite que ![]() car sinon
car sinon ![]() .
.
On rappelle que si ![]() ,
, ![]() .
.
donc si ![]()
![]()
Si ![]() ,
, ![]() ,
,
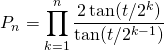
Puis avec ![]() ,
,
 ,
,
![]() .
.
![]()
On rappelle que ![]() ,
,
donc ![]()
![]()
![]()
donc ![]() .
.
9. La même suite à deux périodes différentes de l’année
Version premier semestre
Si ![]() ,
,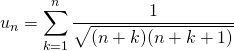 .
.
La suite ![]() est convergente. Vrai ou Faux ?
est convergente. Vrai ou Faux ?
Correction : ![]()
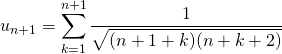
⚠️ à bien remplacer ![]() par
par ![]() à trois emplacements !
à trois emplacements !
Puis en posant ![]() ,
,
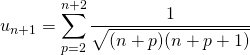
![]() On note
On note ![]()
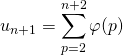
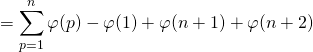
donc ![]()
![]()
![]()
![]()
![]()
![]() où
où ![]()
puis ![]()
et ![]()
donnent ![]() et
et ![]() .
.
La suite est croissante.
![]()
![]() est la somme de
est la somme de ![]() termes tous inférieurs ou égaux à
termes tous inférieurs ou égaux à ![]() , donc
, donc ![]() .
.
La suite est croissante et majorée par 1, elle converge.
Version deuxième semestre
Si ![]() ,
, 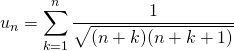 .
.
La suite converge vers ![]() .
.
Vrai ou Faux ?
Correction : ![]() Pour tout
Pour tout ![]() ,
,
![]()
donc ![]()
![]()
par somme, on écrit ![]()
avec 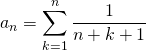
et 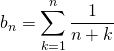 .
.
![]() On remarque en posant
On remarque en posant ![]()
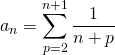
![]() .
.
![]() Puis en notant
Puis en notant ![]() ,
,
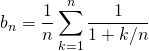
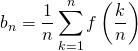 .
.
On reconnaît une somme de Riemann associée à la fonction ![]() continue sur
continue sur ![]() , donc
, donc ![]()
![]() .
.
![]() Puis comme
Puis comme ![]()
par encadrement, la suite ![]() converge vers
converge vers ![]() .
.
10. Deux exercices théoriques (correction dans l’application mobile)
Exercice 1
Soit ![]() une suite réelle bornée et
une suite réelle bornée et ![]() .
.
Si toutes les suites extraites et convergentes de ![]() convergent vers
convergent vers ![]() , la suite
, la suite ![]() converge vers
converge vers ![]() .
.
Exercice 2
Si la suite ![]() converge et ne prend qu’un nombre fini de valeurs, elle est stationnaire.
converge et ne prend qu’un nombre fini de valeurs, elle est stationnaire.
11. Exercices Supplémentaires (correction dans l’application mobile)
1. Exercice 1
Suite définie par ![]() et
et ![]() où
où ![]() .
.
Question 1
Il y a ![]() suites constantes.
suites constantes.
Question 2
Si ![]() , la suite converge vers ?
, la suite converge vers ?
Question 3
Si ![]() ,
, ![]() converge, vrai ou faux ?
converge, vrai ou faux ?
2. Exercice 2
Soit la suite définie par ![]() et
et ![]() où
où ![]() .
.
Question 1
![]() admet deux points fixes vérifiant
admet deux points fixes vérifiant ![]() vrai ou faux ?
vrai ou faux ?
Question 2
La suite est stationnaire pour ![]() valeurs initiales positives de
valeurs initiales positives de ![]() . vrai ouf aux ?
. vrai ouf aux ?
Question 3
![]() est du signe de
est du signe de ![]() , vrai ou faux ?
, vrai ou faux ?
Question 4
Si ![]() , la suite converge, vrai ou faux ?
, la suite converge, vrai ou faux ?
Question 5
Si ![]() ,
, ![]() diverge vers
diverge vers ![]() .
.
Question 6
Si ![]() ,
, ![]() diverge ?
diverge ?
3. Un autre exemple de fonction décroissante
La suite définie par ![]() et
et ![]() où
où ![]() est convergente ssi elle est stationnaire. Vrai ou Faux ?
est convergente ssi elle est stationnaire. Vrai ou Faux ?
4. Exercice
Question 1
Les relations ![]() et
et ![]() où
où ![]() définissent une suite. Vrai ou Faux ?
définissent une suite. Vrai ou Faux ?
Question 2
Si ![]()
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Question 3
La suite ![]() converge vers ?
converge vers ?
5. Exercice 5 avec un calcul numérique
Soit la suite définie par ![]() et
et ![]() où
où ![]()
Question 1
Montrer que ![]() admet un unique point fixe
admet un unique point fixe ![]() .
.
Montrer que si ![]() ,
, ![]()
En déduire la convergence de la suite.
Question 2
Donner un intervalle de longueur inférieure à ![]() contenant la limite de la suite.
contenant la limite de la suite.
6. Exercice 6
Soit la suite définie par ![]() et
et ![]() où
où ![]() .
.
Question 1
La suite ![]() est bien définie et minorée par un réel strtictement positif. Vrai ou Faux ?
est bien définie et minorée par un réel strtictement positif. Vrai ou Faux ?
Question 2
Si la suite converge, sa limite est égale à ![]()
Question 3
Si ![]()
![]() .
.
Question 4
La suite converge.
7. Dernier exemple
Soit la suite définie par ![]() et
et ![]() où
où ![]() .
.
Question 1
Étudier les variations de ![]() et le signe de
et le signe de ![]() .
.
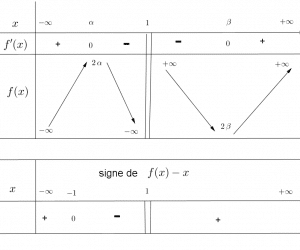
Question 2
L’intervalle ![]() est
est ![]() -stable et on peut en déduire que la suite converge.
-stable et on peut en déduire que la suite converge.
Question 3
L’intervalle ![]() est
est ![]() -stable et on peut en déduire que la suite converge.
-stable et on peut en déduire que la suite converge.
Boostez vos résultats ainsi que votre moyenne en MPSI, PCSI et PTSI avec les cours en ligne et les exercices corrigés au programme de Maths :

