Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Trigonométrie en Maths Sup MPSI, PCSI, MP2I et PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Trigonométrie en Maths Sup
Fonctions circulaires
Plan :
1. Fonction sinus
2. Fonction cosinus
3. Fonction tangente
1. Fonction sinus
![]() Propriétés des angles
Propriétés des angles
Pour tout réel ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Les angles remarquables
Les angles remarquables
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Étude de la fonction
Étude de la fonction
![]()
![]() est continue, strictement croissante sur
est continue, strictement croissante sur ![]() .
.
![]() la dérivée de
la dérivée de ![]() est
est ![]() .
.
![]() Le graphe de
Le graphe de ![]() est symétrique par rapport à
est symétrique par rapport à ![]() et par rapport à la droite d’équation
et par rapport à la droite d’équation ![]() .
.
2. Fonction cosinus
![]() Propriétés des angles
Propriétés des angles
Pour tout réel ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Lien entre
Lien entre ![]() et
et ![]()
Pour tout ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Les angles remarquables
Les angles remarquables
![]()
![]()
![]()
![]()
![]()
![]()
![]()
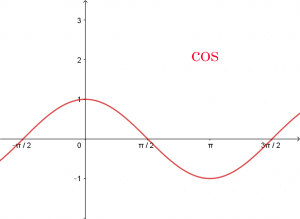
![]() Étude de la fonction
Étude de la fonction
![]()
![]() est continue, strictement décroissante sur
est continue, strictement décroissante sur ![]() .
.
![]() la dérivée de
la dérivée de ![]() est
est ![]()
![]() Le graphe de
Le graphe de ![]() est symétrique par rapport à
est symétrique par rapport à ![]() et par rapport à la droite d’équation
et par rapport à la droite d’équation ![]() .
.
3. Fonction tangente
Elle est définie sur ![]() par
par ![]() .
.
![]() Propriétés des angles
Propriétés des angles
Pour tout réel ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() Les angles remarquables
Les angles remarquables
![]()
![]()
![]()
![]()
![]()
![]()
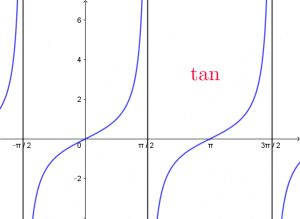
![]() Étude de la fonction
Étude de la fonction
![]()
![]() est continue, strictement croissante sur
est continue, strictement croissante sur ![]() .
.
![]() La dérivée de
La dérivée de ![]() est
est ![]() .
.
![]()
![]() .
.
![]() .
.
![]() Le graphe de
Le graphe de ![]() est symétrique par rapport à
est symétrique par rapport à ![]() .
.
Les droites d’équations ![]() où
où ![]() sont asymptotes à la courbe.
sont asymptotes à la courbe.
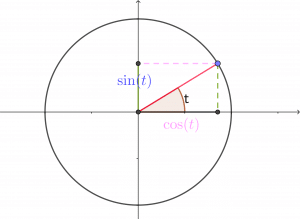
4. S’aider du cercle trigonométrique
On peut retrouver les valeurs liant les ![]() et
et ![]() des angles
des angles ![]() et
et ![]() ,
, ![]() et
et ![]()
![]() et
et ![]() , en plaçant les points correspondants sur le cercle trigonométrique.
, en plaçant les points correspondants sur le cercle trigonométrique.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Méthodes
Plan :
1. Retrouver les formules
2. Équations de base
3. Calcul de ![]() et
et ![]() .
.
Le temps dépend de vos capacités à retenir les formules.
1. Retrouver les formules.
Il faut apprendre ces fichues formules, rien de pire à l’oral qu’un étudiant coincé devant une formule de trigonométrie, les jurys trépignent !
Devoir les retrouver c’est
a) perdre un temps précieux
b) et surtout ne pas avoir idée de transformations qui pourraient débloquer les calculs !
Ce paragraphe indique comment retrouver ces formules à partir des formules d’Euler :
![]()
![]()
![]()
et de la relation : ![]() .
.
1.1. Valeur de  de
de 
![]() M1. somme
M1. somme
![]()
![Rendered by QuickLaTeX.com \cos(a + b) = <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f4fe2391bb9b88bfae89dec46f4ec895_l3.png" height="725" width="725" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[\quad \quad \quad \cos(a) \, \cos(b) - \sin(a) \, \sin(b) $ $\ast$ $\sin(a + b) =$ $ \quad \quad \quad \sin(a) \, \cos(b) + \sin(b) \, \cos(a) $ On utilise $\textrm{e} ^{\textrm{i} \, a} \, \textrm{e} ^{\textrm{i} \, b} = \textrm{e} ^{\textrm{i} \, (a + b)}$, soit $\cos(a + b) + \textrm{i} \, \sin(a + b) = $ $\quad \quad \quad (\cos a + \textrm{i} \, \sin a )(\cos b + \textrm{i} \, \sin b)$ et on termine en égalant les parties réelles et imaginaires. $\bullet$ <b>M2.</b><b> différence</b> $\ast$ $\cos(a - b) = $ $ \quad \quad \quad \cos(a) \, \cos(b) + \sin(a) \, \sin(b) $ $\ast$ $\sin(a - b) =$ $ \quad \quad \quad \sin(a) \, \cos(b) - \sin(b) \, \cos(a) $ en utilisant $M1$ en remplaçant $b$ par $-b$ sans oublier que $\cos$ est paire et $\sin $ est impaire. $\bullet$<b> M3.</b> Et les conséquences : $\quad \ast$ $\cos( 2\, a) = \cos^2(a) - \sin^2(a)$ $\quad \ast$ $\cos(2 \, a) = 2 \cos ^2 (a) - 1$ $\quad \ast$ $\cos(2 \,a) = 1 - 2 \sin ^2(a)$ $\quad \ast$ $\sin(2\, a) = 2 \, \sin(a) \, \cos(a)$ qui peuvent bien sûr s'écrire aussi $\quad \ast$ $\cos ^2 (t) = \displaystyle \frac {\cos(2 \,t) + 1} 2$ $\quad \ast$ $\sin ^2(t) = \displaystyle \frac {1 - \cos(2 \, t)} 2$. $\bullet$ <b>M</b><b>4. </b>sous réserve de définition des trois tangentes : $\ast$ $ \tan(a + b) = \displaystyle \frac {\tan(a) + \tan(b)} {1 - \tan(a) \, \tan(b)} $ obtenue en faisant le quotient des formules de M1 puis en divisant numérateur et dénominateur par $\cos(a) \, \cos(b)$. $\bullet$ <b>M5. </b>en conséquence de M4 sous réserve de définition des trois tangentes : $\ast$ $\tan(a - b) = \displaystyle \frac {\tan(a) - \tan(b)} {1 + \tan(a) \, \tan(b)} $ $\ast$ $\tan(2\, a) = \displaystyle \frac {2 \, \tan(a)} {1 - \tan^2(a)}$ en remplaçant $b$ par $-b$ et en utilisant $\tan$ est une fonction impaire. puis en posant $b = a$ dans la formule de M4. Il y a des cas où il est préférable de s'affranchir de ces formules <b>a) </b>Si $n \in \mathbb{Z}$ et $x \in \mathbb{R}$, $\quad \ast$ $\cos(n\, \pi + x) = (- 1) ^n \cos(x) $ $\quad \ast$ $\sin(n \, \pi + x) = (-1) ^n \, \sin(x)$ <b>b)</b> $\ast$ $\displaystyle \cos \left (\frac {\pi} 2 + x \right) = - \sin(x)$, $\quad \; \ast \displaystyle \sin \left ( \frac {\pi} 2 + x \right ) = \cos(x)$ <b>c)</b> $\ast$ $\displaystyle \cos \left (\frac {\pi} 2 - x \right) = \sin(x)$, $\quad \; \ast \displaystyle \sin \left ( \frac {\pi} 2 - x \right ) = \cos(x)$. <em>La démonstration :</em> <b>a) S</b>i $n$ est pair, $\cos(x + n \,\pi) = \cos(x)$ et $\sin(x + n\, \pi) = \sin(x)$ Si $n$ est impair, $\cos(x + n \, \pi) = \cos(x + \pi ) = - \cos(x) $ et $\sin(x + n \, \pi) = \sin(x + \pi ) = - \sin(x) $ . De plus $(- 1) ^n = - 1$ <b>b)</b> La dérivée de $u : x \mapsto \cos(x)$ peut s'écrire $u'(x) = -\sin(x) = \cos(x + \pi/2)$ la dérivée de $v : x \mapsto \sin(x)$ peut s'écrire $v'(x) = \cos(x) = \sin(x + \pi/2)$ <b>c)</b> à l'aide d'un dessin du cercle trigonométrique ou en remplaçant $x$ par $-x$ dans les formules du b). <h4><b>1.2. Linéarisation</b></h4> $\bullet$ <b>M6 Formules au programme </b> $\ast$ $2 \, \cos(a) \, \cos(b) = $ $\quad \quad \quad \quad \cos(a + b) + \cos(a - b) $ $\ast$ $2 \, \sin(a) \, \sin(b) =$ $ \quad \quad \quad \quad \cos(a - b) - \cos(a + b)$ $\ast$ $2 \, \sin(a) \cos(b) = $ $ \quad \quad \quad \quad \sin(a + b) + \sin(a - b) $ <em>La justification :</em> $\bullet$ Par M1 et M2 $\cos(a + b) = \cos(a) \, \cos(b) - \sin(a) \, \sin(b) $ et $\cos(a - b) = \cos(a) \, \cos(b) + \sin(a) \, \sin(b) $ Par <a href="https://groupe-reussite.fr/ressources/cours-en-ligne-sommes-produits-maths-sup/">somme</a> et différence : $\cos(a + b) + \cos(a - b) = 2 \, \cos(a) \, \cos (b)$ $\cos(a - b) - \cos(a - b) = 2 \, \sin(a) \, \sin (b)$ $\bullet$ Par M1 et M2 $\sin(a + b) = \sin(a) \, \cos(b) + \sin(b) \, \cos(a) $ et $\sin(a - b) = \sin(a) \, \cos(b) - \sin(b) \, \cos(a) $ et on additionne $\sin(a + b) + \sin(a - b) = 2 \sin(a) \, \cos(b)$. $\bullet$ <b>M7. Formules à retrouver </b> $\ast$ $\cos(p) + \cos(q) = $ $ \quad \quad \quad 2 \, \displaystyle \cos \left ( \frac {p + q} 2 \right ) \, \cos \left ( \frac {p - q} 2 \right ) $ $\ast$ $\cos(p) - \cos(q) = $ $ \quad \quad \quad - 2 \, \displaystyle \sin \left ( \frac {p + q} 2 \right ) \, \sin \left ( \frac {p - q} 2 \right ) $ $\ast$ $\sin(p) + \sin(q) =$ $ \quad \quad \quad 2 \, \displaystyle \sin \left ( \frac {p + q} 2 \right ) \, \cos \left ( \frac {p - q} 2 \right ) $ et en remplaçant $q$ par $- q$, $\ast$ $\sin(p) - \sin(q) = $ $ \quad \quad \quad 2\, \displaystyle \sin \left ( \frac {p - q} 2 \right ) \, \cos \left ( \frac {p + q} 2 \right ) $. <em>la démonstration :</em> On pose $p = a + b $ et $q =a - b $ ssi $ a = (p + q)/2$ et $b = (p - q) /2$ Les formules de M6 $\cos(a + b) + \cos(a - b) = 2 \, \cos(a) \, \cos (b)$ $\cos(a - b) - \cos(a - b) = 2 \, \sin(a) \, \sin (b)$ deviennent $\cos(p) + \cos(q) = $ $ \quad \quad 2 \, \displaystyle \cos \left ( \frac {p + q} 2 \right ) \, \cos \left ( \frac {p - q} 2 \right ) $ $\cos(p) - \cos(q) = $ $ \quad \quad - 2\, \displaystyle \sin \left ( \frac {p + q} 2 \right ) \, \sin \left ( \frac {p - q} 2 \right ) $ <em>La formule :</em> $\sin(a + b) + \sin(a - b) = 2 \sin(a) \, \cos(b)$. devient $\sin(p) + \sin(q) =$ $ \quad \quad 2\, \displaystyle \sin \left ( \frac {p + q} 2 \right ) \, \cos \left ( \frac {p - q} 2 \right ) $. <h4><b>1.3. Utilisation de</b> $t = \tan(x /2)$</h4> En posant $t = \displaystyle \tan \left ( \frac x 2 \right ) $, on démontre $\quad \ast$ $\cos(x) = \displaystyle \frac {1 - t ^2} {1 + t ^2} $ $\quad \ast$ $\sin(x) = \displaystyle \frac {2\, t} {1 + t ^2} $ $\quad \ast$ $\tan(x) = \displaystyle \frac {2\, t} {1 - t ^2} $. <em>la démonstration :</em> On utilise l'angle double et les résultats de M3 $\cos(x) = 2 \cos^2(x / 2) - 1$ et $\cos^2(x / 2) = \displaystyle \frac 1 { 1 + \tan^2(x/2) } = \frac 1 {1 + t ^2}$ $\cos(x) = \displaystyle \frac 2 {1 + t ^2} - 1 = \frac {1 - t ^2} {1 + t^2}$ et M5 $\tan(x) = \displaystyle \frac {2 \, \tan(x /2)} {1 + \tan^2(x/2)} = \frac {2 \, t } {1 + t^2}$ Puis on termine avec $\quad \quad \sin(x) = \cos(x) \, \tan(x)$. <h4><b>1.4. Transformation de</b> $A \cos(x) + B \sin(x)$<b> si </b>$(A , B) \neq (0 , 0)$</h4> Introduire la forme trigonométrique de $ A + \textrm{i} \, B = \rho \, \textrm{e} ^{\textrm{i} \, \varphi}$ $A \cos(x) + B \sin(x) =$ $ \quad \quad \rho \left ( \cos(\varphi) \, \cos(x) + \sin(\varphi) \, \sin(x) \right ) $ $ A \cos(x) + B \sin(x) = \rho \cos(x -\varphi ) $. <h3>2. Équations de base</h3> <div> $\bullet $<b> E1 </b>avec des cosinus : $\ast$ $\cos(x) = \cos(y)$ $\quad \Leftrightarrow $ $ \exists\, k \in \mathbb{Z}, \, x = y + 2 \, k \, \pi$ $\quad \; \textrm{ou } \exists\, p \in \mathbb{Z}, \, x = - y + 2 \, p\, \pi$ $\ast$ Si $a \in \, [- 1 \,, \, 1]$, $\cos(x) = a$ $\quad \Leftrightarrow $ $ \exists\, k \in \mathbb{Z}, \, x = \textrm{Arccos } a + 2 \, k\, \pi$ $\quad \; \textrm{ou } \exists\, p \in \mathbb{Z}, \, x = - \textrm{Arccos } a + 2 \, p\, \pi$. $\bullet$ <b>E2</b> avec des sinus $\sin(x) = \sin (y)$ $\quad \Leftrightarrow $ $ \exists\, k \in \mathbb{Z}, \, x = y + 2 \, k \pi\]" title="Rendered by QuickLaTeX.com"/>\quad \; \textrm{ou } \exists\, p \in \mathbb{Z}, \, x = \pi - y + 2 \, p \pi](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c3d71033e17cb747119ba9997a538675_l3.png)
![]() Si
Si ![]() ,
,
![]()
![]()
![]()
![]()
![]() E3 avec des tangentes
E3 avec des tangentes
![]()
![]()
![]()
![]()
![]() Si
Si ![]() ,
,
![]()
![]()
![]() .
.
Lorsque les équations sont « compliquées », il y a moins de risque d’erreur à utiliser des égalités à ![]() ou
ou ![]() près plutôt que les modulos.
près plutôt que les modulos.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
3. Calcul de  et
et 
Il faut savoir au moins traiter le cas du calcul de ![]() ou de
ou de ![]() lorsque
lorsque ![]() est un entier donné « faible ».
est un entier donné « faible ».
Le calcul dans le cas général comme il est donné ci-dessous pourrait faire l’objet d’une question de sujet de concours.
On utilise les formules de Moivre et la formule du binôme de Newton
![]()
On sépare les indices ![]() des indices
des indices ![]() , pour comparer les parties réelles et imaginaires.
, pour comparer les parties réelles et imaginaires.
![]()
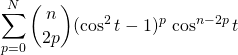
![]()
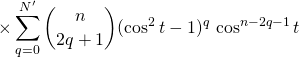
avec ![]() et
et ![]() .
.
la démonstration complète :
Par la formule de Moivre, 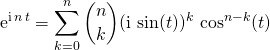
On sépare les indices ![]() avec
avec ![]()
soit pour ![]() avec
avec ![]()
des indices ![]() avec
avec ![]()
soit pour ![]() où
où ![]()
ce qui permet de séparer la partie réelle de la partie imaginaire
![]() avec
avec
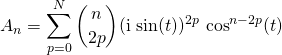
et ![]()
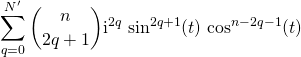
On simplifie ces écritures :
![]()
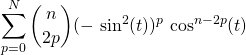
![]()
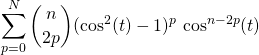
![]()
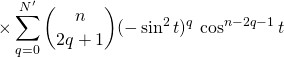
![]()
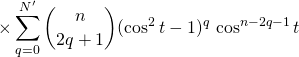
Pour prendre de l’avance ou faire face à vos difficultés, retrouvez d’autres cours en ligne de maths et cours de maths à domicile pour les PCSI, PTSI et MPSI :

