Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés de Trigonométrie en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Equation, Inéquations, Linéarisation
1. Des calculs
2. Des équations
3. Des inéquations
4. Systèmes d’équations
5. Linéarisation
1. Des calculs de trigonométrie en maths sup
Exercice 1
Trouver ![]() tel que
tel que ![]() . On utilisera
. On utilisera ![]() .
.
On obtient ![]()
avec ![]()
Correction : ![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]() On a obtenu :
On a obtenu :
![]()
donc ![]()
ou ![]() ,
,
ce qui donne
![]()
ou ![]()
![]() et
et ![]()
Il n’y a aucune valeur de ![]() donnant une valeur de la forme
donnant une valeur de la forme ![]() dans
dans ![]() .
.
La seule valeur de la forme ![]() dans
dans ![]() est obtenue pour
est obtenue pour ![]()
Donc ![]() .
.
Exercice 2
Soient ![]() et
et ![]() dans
dans ![]() vérifiant
vérifiant ![]() et
et ![]() .
.
a) En utilisant ![]() , calculer
, calculer ![]() .
.
Correction : ![]()
![]()
![]() .
.
On en déduit qu’il existe ![]() tel que
tel que ![]() .
.
On remarque que ![]() et
et ![]() donc
donc ![]() .
.
![]() est la seule valeur de la forme
est la seule valeur de la forme ![]() dans l’intervalle
dans l’intervalle ![]() , donc
, donc ![]() .
.
b) Calculer ![]() .
.
Soit ![]() tel que
tel que ![]() . Exprimer
. Exprimer ![]() et
et ![]() en fonction de
en fonction de ![]() .
.
Correction : On a vu que ![]() avec
avec ![]() donc
donc ![]() .
.
![]()
![]() .
.
Comme ![]() car
car ![]() .
.
![]()
avec ![]() , donc
, donc ![]()
Comme ![]() ,
, ![]() .
.
On a prouvé que ![]() et
et ![]() .
.
Exercice 3
Soit ![]() .
.
Calculer ![]() .
.
En déduire la valeur de ![]() .
.
Correction : On utilise ![]()
![]()
![]()
donc ![]() .
.
Donc en posant ![]() ,
, ![]() donne
donne ![]() soit
soit ![]() .
.
Cette équation admet deux racines dont une seule est positive :
on en déduit que ![]() .
.
Exercice 4
Calculer ![]() puis
puis ![]() .
.
Correction : On utilise la formule ![]() d’abord pour
d’abord pour ![]() et on pose
et on pose ![]()
![]()
ce qui donne ![]()
soit ![]() .
.
cette équation a deux racines : ![]() et
et ![]() ,
,
donc ![]() .
.
On réutilise la même méthode en posant ![]() .
.
On obtient l’équation ![]()
soit ![]()
admet un discriminant ![]()
Une seule des racines est positive :
![]()
puis ![]()
![]() .
.
![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Équations
Exercice 1
Résoudre ![]()
Correction : ![]()
ssi ![]()
ssi ![]()
ou ![]()
ssi ![]()
ou ![]()
ssi ![]()
ou ![]() .
.
Exercice 2
Ensemble des réels ![]() tels que l’équation
tels que l’équation
![]()
![]() .
.
ait des solutions.
Les déterminer.
Correction : Pour que l’équation ait un sens, il est nécessaire que ![]() .
.
Comme ![]() , il existe
, il existe ![]() tel que
tel que
![]() et
et ![]() .
.
L’équation s’écrit alors
![]() .
.
Elle admet des solution ssi ![]()
ssi ![]()
et ![]() .
.
![]()
![]() est racine évidente de
est racine évidente de ![]() et on peut écrire :
et on peut écrire :
![]()
![]()
donc ![]() ssi
ssi ![]() .
.
![]()
![]() est racine évidente de
est racine évidente de ![]() et on peut écrire :
et on peut écrire :
![]()
![]()
donc ![]() ssi
ssi ![]() .
.
L’équation a toujours des solutions lorsque ![]() .
.
On transforme
![]()
![]()
![]()
![]()
L’équation est donc équivalente à
![]()
ssi ![]()
ou ![]()
ssi ![]()
ou ![]() .
.
Exercice 3
Résoudre ![]()
Correction : ![]()
![]()
![]()
![]()
![]()
l’équation est équivalente à
![]()
ssi ![]()
ou ![]()
ssi ![]()
ou ![]() .
.
Exercice 4
Résoudre ![]()
Correction : ![]() Première méthode
Première méthode
On pose ![]()
![]()
ssi ![]()
ssi ![]()
L’équation ![]() admet une seule racine positive
admet une seule racine positive ![]()
![]() ssi
ssi ![]() ou
ou![]() ou
ou ![]() .
.
On introduit ![]() tel que
tel que ![]()
Les solutions sont les réels ![]() ,
, ![]() et
et ![]() lorsque
lorsque ![]()
![]() Autre méthode
Autre méthode
![]()
![]()
![]()
et comme ![]() , l’équation est équivalente à
, l’équation est équivalente à
![]() ou
ou ![]()
![]()
La deuxième équation s’écrit
![]()
L’équation ![]() admet une seule racine dans
admet une seule racine dans ![]() :
: ![]()
On note ![]() tel que
tel que ![]() .
.
L’ensemble des solutions est formé par les réels
![]()
![]() où
où ![]()
![]()
![]() où
où ![]()
![]()
![]() où
où ![]() .
.
On pourra choisir ![]() .
.
3. Inéquations
Exercice 1
Résoudre l’inéquation
![]() .
.
Correction : On cherche la forme trigonométrique de 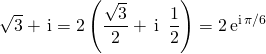 .
.
![]()
![]()
![]()
On doit donc résoudre :
![]()
ssi ![]()
ssi ![]()
ssi ![]()
Exercice 2
Résoudre ![]()
Correction : Les racines de l’équation ![]()
sont ![]() et
et ![]()
donc ![]()
et on doit résoudre :
![]()
ssi ![]()
ssi ![]()
ssi ![]()
Exercice 3
Résoudre si ![]() ,
,
![]()
![]() .
.
Correction : On note ![]()
![]()
et en utilisant ![]() pour transformer
pour transformer ![]() et
et ![]() ,
,
![]()
![]()
donc ![]() s’écrit
s’écrit ![]()
en utilisant ensuite
![]()
![]() .
.
On cherche les ![]() qui vérifient
qui vérifient ![]() .
.
![]()
![]() ssi
ssi ![]() où
où ![]() .
.
![]() s’annule et change de signe en ces 4 points et est strictement positif sur
s’annule et change de signe en ces 4 points et est strictement positif sur ![]() .
.
![]()
![]() ssi
ssi ![]() ou
ou ![]() .
.
![]() s’annule et change de signe en ces 2 points et est strictement positif sur
s’annule et change de signe en ces 2 points et est strictement positif sur ![]() .
.
![]()
![]() ssi
ssi ![]() .
.
ce dernier facteur est strictement positif sur ![]() .
.
On utilise le tableau de signes qui suit pour donner l’ensemble des solutions lorsque ![]() .
.
Dans ce tableau, on fait apparaître les valeurs annulant ![]() et on écrit trois lignes résumant les signes des trois facteurs étudiés ci-dessus.
et on écrit trois lignes résumant les signes des trois facteurs étudiés ci-dessus.
L’ensemble des solutions est défini par
![]() .
.

4. Système d’équations
Exercice 1
Si ![]() est un réel donné, résoudre le système
est un réel donné, résoudre le système ![]() :
:
![]()
Correction : ![]()
![]() est équivalent à l’équation obtenue en prenant la somme de la première équation et de
est équivalent à l’équation obtenue en prenant la somme de la première équation et de ![]() fois la deuxième soit à
fois la deuxième soit à
![]()
soit en multipliant par ![]() :
:
![]()
![]()
en égalant les parties réelles et imaginaires, on obtient le système :
![]() (1)
(1)
![]() (2)
(2)
![]()
![]() est impossible car l’équation (1) donnerait
est impossible car l’équation (1) donnerait ![]()
donc (2) est équivalent à
![]()
ssi ![]() .
.
![]() Alors (1) s’écrit
Alors (1) s’écrit
![]() (1)
(1)
ssi ![]()
![]() cas
cas ![]()
![]()
ssi ![]() (a)
(a)
ou ![]() (b)
(b)
avec ![]() (c)
(c)
par somme et différence de (c) et (a), on obtient :
![]()
et ![]()
puis avec (c) et (b) :
![]()
et ![]()
![]() cas
cas ![]()
![]()
ssi ![]() (a)
(a)
ou ![]() (b)
(b)
avec ![]() (c)
(c)
Par somme et différence de (c) et (a), on obtient : ![]()
et ![]()
soit
![]()
et ![]()
puis avec (c) et (b), ![]()
et ![]() .
.
soit
![]()
et ![]() .
.
Les couples solutions sont les couples
![]()
![]()
![]()
![]()
où ![]() .
.
⚠️ N’oubliez pas de faire la synthèse des différents cas !
⚠️ Il ne faut surtout pas raisonner avec les modulos dans un problème faisant intervenir des sommes ou des différences d’équations valables modulo ![]() ou
ou ![]() .
.
Par exemple, en notant ![]() , si l’on écrivait le premier groupe de solutions sous la forme :
, si l’on écrivait le premier groupe de solutions sous la forme :
![]() et
et ![]() ,
,
le couple ![]() serait solution alors qu’il est impossible de l’écrire sous la forme
serait solution alors qu’il est impossible de l’écrire sous la forme ![]() puisque
puisque ![]() et
et ![]() n’admet pas de solution entière.
n’admet pas de solution entière.
Exercice 2
Résoudre si ![]() est un réel donné le système
est un réel donné le système ![]() :
:
![]()
Correction : ![]() est équivalent à l’équation obtenue en prenant la somme de la première équation et de
est équivalent à l’équation obtenue en prenant la somme de la première équation et de ![]() fois la deuxième soit à
fois la deuxième soit à
![]()
![]()
ssi
![]()
![]()
On distingue alors deux cas
![]() Cas 1
Cas 1
![]()
et ![]()
![]() donne
donne
![]()
et (1) donne l’existence de ![]() tel que
tel que
(1 a) ![]()
ou
(1 b) ![]()
![]() en formant la somme et la différence de (1a) et (2), on obtient :
en formant la somme et la différence de (1a) et (2), on obtient :
![]()
![]()
![]() en formant la somme et la différence de (1b) et (2), on obtient :
en formant la somme et la différence de (1b) et (2), on obtient :
![]()
![]()
![]() Cas 2
Cas 2
![]()
et ![]()
![]() donne
donne ![]()
et (3) donne l’existence de ![]() tel que
tel que
(3 a) ![]()
ou
(3 b) ![]()
![]() en formant la somme et la différence de (3a) et (4), on obtient
en formant la somme et la différence de (3a) et (4), on obtient
![]()
![]()
![]() en formant la somme et la différence de (3b) et (4), on obtient
en formant la somme et la différence de (3b) et (4), on obtient
![]()
![]()
Les couples solutions sont les couples
![]()
![]()
![]()
![]()
où ![]() .
.
⚠️ Les remarques faites à la fin de l’exercice 1 restent valables ici.
Exercice 3
Résoudre le système :
![]() .
.
Correction : ![]() On utilise
On utilise ![]()
![]()
![]()
![]()
![]()
![]() Le système
Le système
![]()
donne ![]() et
et ![]()
![]() Le système
Le système
![]()
donne ![]() et
et ![]()
![]() Les couples solutions sont
Les couples solutions sont ![]()
![]()
où ![]()
⚠️ Il ne faut surtout pas raisonner avec les modulos dans un tel problème car on perdrait la condition ![]() .
.
👍 La méthode utilisée ici est plus simple que l’utilisation de la première équation pour écrire la deuxième équation sous la forme ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
5. Linéarisation
Question 1.
Linéarisation de ![]() lorsque
lorsque ![]() et
et ![]() .
.
Correction : On utilise les formules d’Euler :
![]()
puis le binôme de Newton :
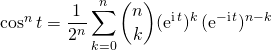
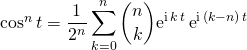
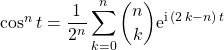
et en prenant la partie réelle
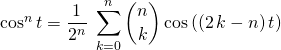
👍 Le principe est bien sûr le même pour obtenir par exemple ![]() ou
ou ![]() .
.
Vérifiez que vous savez le faire !
Simplifier le résultat précédent pour
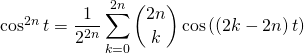
On transforme
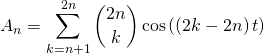
en posant ![]()
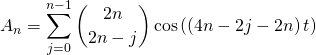
par propriété du coefficient du binôme
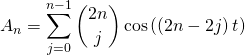
et par parité de la fonction ![]()
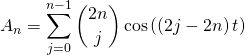 .
.
Puis en considérant le terme pour ![]() de la somme :
de la somme :
![]()
![]()
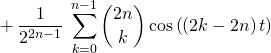
Question 3
Simplifier l’écriture de ![]() .
.
Correction : Valeur de ![]()
![]()
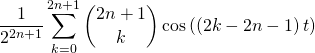
On transforme
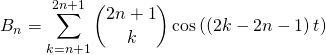
en posant ![]()
avec le même type de calculs que dans le cas pair :
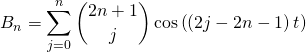
donc
![]()
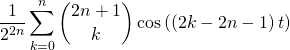
Ne prenez pas de retard et découvrez dès maintenant les chapitres au programme de Maths à venir en MPSI, PTSI et PCSI :

